Mesh -analysekonsepter, metoder, eksempler

Han Mesh -analyse Det er en teknikk som brukes til å løse flate elektriske kretsløp. Denne prosedyren kan også vises i litteraturen med metodens navn på kretsstrømmer o Metode for Mesh -strømmer (eller loop).

Grunnlaget for denne og andre metoder for elektrisk kretsanalyse er i lovene i Kirchhoff og Ohms lov. Kirchhoffs lover på sin side er uttrykk for to veldig viktige bevaringsprinsipper i fysikk for isolerte systemer: både elektrisk ladning og energi er bevart.

Figur 1. Kretsene er en del av utallige enheter. Kilde: Pixabay.

På den ene siden er den elektriske ladningen relatert til strømmen, som beveger belastningen, mens energien i en krets er knyttet til spenningen, som er middelet som er ansvarlig for å gjøre det nødvendige arbeidet for å holde belastningen i bevegelse.

Disse lovene, brukt på en flat krets, genererer et sett med samtidige ligninger som må løses for å oppnå strøm- eller spenningsverdier.

Ligningssystemet kan løses med allerede kjente analytiske teknikker, for eksempel Cramer Rule, som krever beregning av determinanter for å oppnå systemløsningen.

Avhengig av antall ligninger, løses de ved hjelp av en vitenskapelig kalkulator eller en matematisk programvare. På nettverket er det også mange alternativer tilgjengelig.

[TOC]

Viktige vilkår

Før vi forklarer hvordan det fungerer, vil vi begynne med å definere disse vilkårene:

Gren: Seksjon som inneholder et element i kretsen.

Node: punkt som kobler to eller flere grener.

Bånd: Det er enhver lukket del av en krets, som begynner og slutter i samme node.

Mesh: sløyfe som ikke inneholder noe annet binding inne (essensielt nett).

Metoder

Meshealanalysen er en generell metode som tjener til å løse kretsløp hvis elementer er koblet sammen i serie, parallelt eller blandet, det vil si når typen tilkobling ikke er klart utmerket. Kretsen må være flat, eller i det minste må det være mulig å betale tilbake den som sådan.

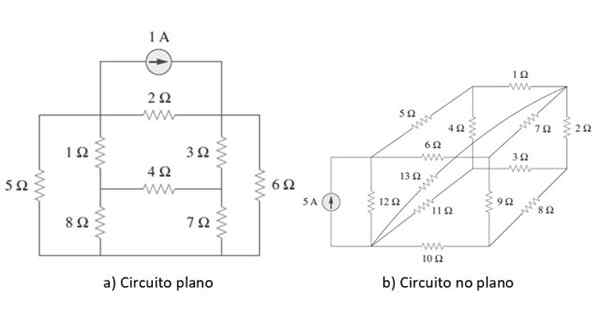Figur 2. Flate og ikke -flatkretser. Kilde: Alexander, C. 2006. Elektriske kretsfundamenter. 3. Utgave. Mc Graw Hill.

Et eksempel på hver type krets er vist på figuren over. Når poenget er avklart, for å begynne, vil vi bruke metoden på en enkel krets som et eksempel i neste avsnitt, men før vi kort gjennomgår lovene til Ohm og Kirchhoff.

Ohms lov: Sean V Spenningen, R motstanden e Yo Strømmen til det ohmiske resistive elementet, der spenningen og strømmen er direkte proporsjonal, og motstanden er proporsjonalitetens konstant:

Kan tjene deg: API Gravity: Skala og klassifisering av råolje

V = i.R

Spenning Kirchhoff Law (LKV): I en hvilken som helst lukket bane som er reist i en retning, er den algebraiske summen av spenningene null. Dette inkluderer spenninger på grunn av kilder, motstander, induktorer eller kondensatorer: ∑ e = ∑ r_Yo. Yo

Kirchhoff of the Current (LKC): I en hvilken som helst node er den algebraiske summen av strømningene null, med hensyn til at strømningene som kommer inn, blir tildelt et skilt og som en annen kommer ut. På denne måten: ∑ i = 0.

Med metoden for nettstrømmer er det ikke nødvendig.

- Trinn for å anvende nettanalyse

Vi vil begynne å forklare metoden for en 2 meshes krets. Prosedyren kan forlenges senere for større kretsløp.

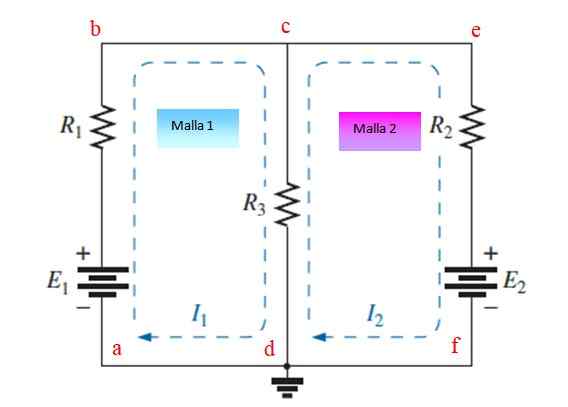Figur 3. Krets med motstand og kilder arrangert i to masker. Kilde: f. Zapata.

Trinn 1

Tilordne og tegne uavhengige strømmer til hvert nett, i dette eksemplet er de Yo₁ og Yo₂. De kan tegnes i en plan eller også anti -Horary.

Steg 2

Bruk Kirchhoff Tensions Law (LTK) og Ohms lov på hvert nett. Potensielle fall tildeles et tegn (-) mens økningene er tildelt tegn (+).

ABCDA Mesh

Med utgangspunkt i punkt A og etter betydningen av strømmen, finner vi en økning i potensialet i batteri E1 (+), deretter et fall i r₁ (-) Og så et nytt fall i r₃ (-).

Samtidig, motstanden r₃ Det krysses også av strøm I₂, Men i motsatt retning representerer det derfor en økning (+). Den første ligningen er slik:

OG₁-R₁.Yo₁ -R₃.Yo₁ + R₃.Yo₂ = 0

Umiddelbart fakturering og re -promoteringsbetingelser:

- (R₁+R₃) Yo₁ +R₃Yo₂ = -E₁  (Ligning 1)

CEFDC -nett 

Starter fra punktet og Og å følge betydningen av strømmen er et potensielt fall i R₂ (-), Nok et fall i OG₂, Siden strømmen kommer inn gjennom batteriets pol + og til slutt nok et fall inn R₃ (-), samtidig strømmen Yo₁ Det krysser R₃ I motsatt retning (+).

Den andre ligningen, med skiltene indikert, forblir på denne måten:

- R₂ Yo₂ - OG₂ -R₃ Yo₂ +R₃ Yo₁= 0

R₃Yo₁ - (R₂ +R₃₎ Yo₂ = E₂  (Ligning 2)

Merk at det er to ligninger med de to ukjente og₁ og jeg₂.

Trinn 3

Deretter blir det dannede ligningssystemet løst.

Løste øvelser

For å starte, er det viktig å ta hensyn til følgende:

-Båndene eller nettstrømmene kan tildeles en vilkårlig retning.

-Til hvert viktig netting - eller "vindu" - at kretsen må tilordnes en strøm.

Kan tjene deg: isokorisk prosess

-Mesh -strømningene kalles med store bokstaver for å skille dem fra strømningene som sirkulerer i grener, selv om strømmen i noen tilfeller sirkulerer gjennom en gren kan det samme som nettet.

- Eksempel 1

Finn strømningene som sirkulerer gjennom hver motstand i kretsen i figur 3, hvis elementene har følgende verdier:

R₁ = 20 Ω; R₂ = 30 Ω; R₃ = 10 Ω; OG₁ = 12 V; OG₂ = 18 v

Løsning

For det første er det nødvendig å tilordne strømmer av netting og₁ og jeg₂ og ta systemet med ligninger som avledet i foregående avsnitt, og erstatt deretter verdiene gitt i uttalelsen:

- (R₁+R₃) Yo₁ +R₃Yo₂ = -E₁  (Ligning 1)

R₃Yo₁ - (R₂ +R₃₎ Yo₂ = E₂     (Ligning 2)

-

-(20+30) Yo₁ + 10i₂ = -12

10i₁ - (30 +10) i₂ = 18      

--

-femtiYo₁ + 10i₂ = -12

10i₁ - 40 i₂ = 18      

Siden det er et system med 2 x 2 -ligninger, kan det lett løses ved reduksjon, multipliserer med 5 den andre ligningen for å eliminere ukjent Yo₁:

-femtiYo₁ + 10 i₂ = -12

50i₁ - 200 i₂ = 90

-     

-190 i₂= 78

Yo₂ = - 78/180 a = - 0.41 a

Strømmen blir umiddelbart tømt Yo₁ av noen av de opprinnelige ligningene:

Yo₁ = (18 + 40 i₂) / 10 = (18 + 40 x (-0.41)) / 10 = 0.16 a

Det negative tegnet i strømmen Yo₂ betyr at strømmen i de 2 nettet sirkulerer i strid med tegningen.

Strømmene i hver motstand er som følger:

For motstand R₁ Strømmen sirkulerer Yo₁ = 0.16 a i den forstand trukket, av motstand R₂ Strømmen sirkulerer Yo₂ = 0.41 a i motsetning til det trukket, og for motstand R₃ sirkulerer Yo₃ = 0.16- (-0.41) A = 0.57 a ned.

Systemløsning etter Cramer's Method

På en matriks måte kan systemet løses som følger:

Trinn 1: Beregn Δ

 Viktig: Når Δ = 0, har systemet ingen løsning, det er et inkompatibelt system.

Trinn 2: Beregn Δ₁

Den første kolonnen erstattes av de uavhengige begrepene i ligningssystemet, og opprettholder rekkefølgen systemet opprinnelig ble hevet:

Trinn 3: Beregn i₁

Yo₁ = Δ₁/Δ = 300/1900 = 0.16 a

Trinn 4: Beregn Δ₂

 Trinn 5: Beregn i₂

Yo₂ = Δ₂/Δ = -780/1900 = -0.41 a

- Eksempel 2

Bestem strømmen og spenningene gjennom hver motstand i den følgende kretsen, ved hjelp av mesh -strømningsmetoden:

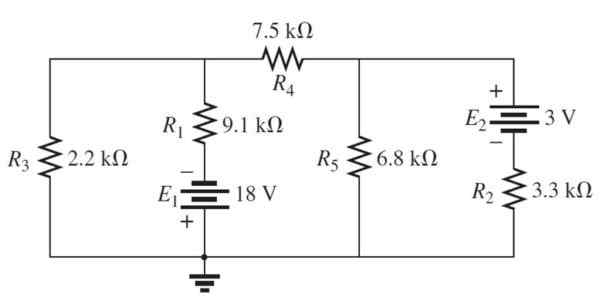Figur 4. 3 Mesh Circuit. Kilde: Boylestad, R. 2011. Introduksjon til kretsanalyse.2. Utgave. Pearson.

Løsning

De tre nettstrømmene er tegnet, som vist i følgende figur, i vilkårlige sanser. Nå kjører nettene hvor som helst:

Det kan tjene deg: imantasjon: hva som består, metode og eksempler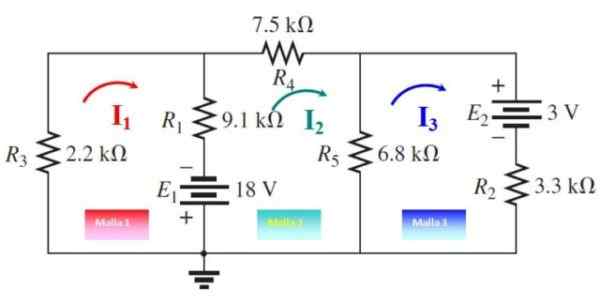 Figur 5. Mesh -strømmer for trening 2. Kilde: f. Zapata, modifisert fra Boylestad.

Mesh 1

-9100.Yo₁+18-2200.Yo₁+9100.Yo₂= 0

-11300 i₁ + 9100.Yo₂ = -18

Mesh 2       

-(7500 +6800 +9100) .Yo₂ + 9100.Yo₁+6800.Yo₃-18 = 0

9100.Yo₁ - 23400.Yo₂ + 6800.Yo₃ = 18

Mesh 3  

-(6800 + 3300) i₃ + 6800.Yo₂ - 3 = 0

6800.Yo₂ - 10100.Yo₃ = 3

Ligningssystem

-11300 i₁ + 9100.Yo₂ + 0.Yo₃= -18

9100.Yo₁ - 23400.Yo₂ + 6800.Yo₃ = 18

0.Yo₁ + 6800.Yo₂ - 10100.Yo₃ = 3

Selv om tallene er store, løses det raskt ved hjelp av en vitenskapelig kalkulator. Husk at ligningene må bestilles og legge til nuller på stedene der det ukjente ikke vises, slik det vises her.

Mesh -strømningene er:

Yo₁ = 0.0012 a; Yo₂ = -0.00048 A; Yo₃ = -0.00062 a

Strømningene Yo₂ og Yo₃ De sirkulerer i motsatt retning i figuren, siden de viste seg å være negative.

Tabell med strømmer og spenninger i hver motstand

Motstand (ω)	Nåværende (forsterkere)	Spenning = i.R (volt)
9100	Yo1 -Yo2 = 0.0012-(-0.00048) = 0.00168	femten.3
3300	0.00062	2.05
2200	0.0012	2.64
7500	0.00048	3.60
6800	Yo2 -Yo3= -0.00048-(-0.00062) = 0.00014	0.95

Cramer Rule Solution

Siden de er store antall, er det praktisk å bruke vitenskapelig notasjon for å jobbe direkte med dem.

Beregning av i₁

Fargepiler i 3 x 3 Determinanten indikerer hvordan du finner numeriske verdier, og multipliserer de angitte verdiene. La oss starte med å skaffe dem av den første braketten i determinanten Δ:

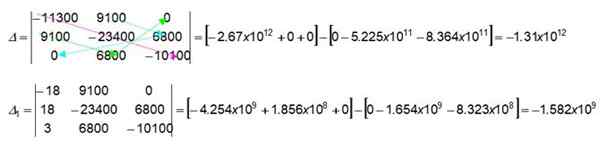
(-11300) x (-23400) x (-10100) = -2.67 x 10¹²

9100 x 0 x 0 = 0

9100 x 6800 x 0 = 0

Vi får umiddelbart den andre braketten i den samme determinanten, som fungerer fra venstre til høyre (for denne braketten ble ikke de fargede pilene trukket på figuren). Vi inviterer leseren til å bekrefte det:

0 x (-23400) x 0 = 0

9100 x 9100 x (-10100) = -8.364 x 10^elleve

6800 x 6800 x (-11300) = -5.225 x 10^elleve

På samme måte kan leseren også bekrefte verdiene for determinanten Δ₁.

Viktig: Mellom begge parentesene er det alltid et negativt tegn.

Endelig oppnås strømmen Yo₁ gjennom Yo₁ = Δ₁ / Δ

Yo₁ = -1.582 x 10⁹/-1.31 x 10¹² = 0.0012 a                                   

Beregning av i₂

Prosedyren kan gjentas for å beregne Yo₂, I dette tilfellet for å beregne determinanten Δ₂ Den andre kolonnen i Δ Determinanten erstattes av kolonnen til de uavhengige begrepene og dens verdi blir funnet, i henhold til fremgangsmåten som er forklart.

Imidlertid, som tungvint på grunn av store antall, spesielt hvis det ikke er noen vitenskapelig kalkulator, er det enkleste å erstatte verdien av Yo₁ Allerede beregnet, i følgende ligning og tydelig:

-11300 i₁ + 9100.Yo₂ + 0.Yo₃= -18 → 9100 I₂= -18 + 11300 i₁ → i₂ = -0.00048 a

I3 beregning

En gang med verdiene til Yo₁ og Yo₂ I hånden, Yo₃ Det er direkte funnet ved erstatning.

Referanser

1. Alexander, ca. 2006. Elektriske kretsfundamenter. 3. Utgave. Mc Graw Hill.
2. Boylestad, r. 2011. Introduksjon til kretsanalyse.2. Utgave. Pearson.
3. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 5. Elektrisk interaksjon. Redigert av Douglas Figueroa (USB).
4. Garcia, l. 2014. Elektromagnetisme. 2. Utgave. Industrial University of Santander.
5. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 2.