Komprimerbarhet av faste stoffer, væsker, gasser, eksempler

De komprimerbarhet av et stoff eller materiale er volumendringen som den opplever når det er underlagt en trykkendring. Vanligvis avtar volumet når du bruker et trykk på et system eller et objekt. Noen ganger oppstår det motsatte: en trykkendring kan imidlertid gi en eksplosjon der systemet øker volumet, eller når en faseendring finner sted.

I noen kjemiske reaksjoner kan dette skje og også i gasser, siden ved å øke frekvensen av kollisjoner, foregår de frastøtende kreftene.

En ubåt opplever kompresjonskrefter når de er nedsenket. Kilde: Pixabay.com.

Ved å forestille deg hvor enkelt eller vanskelig det kan være å komprimere et objekt, må du vurdere de tre statene der saken normalt er: fast, flytende og gassformig. I hver av dem holder molekylene visse avstander fra hverandre. Jo mer faste koblinger som forener stoffmolekylene som utgjør objektet og nærmere er, jo vanskeligere vil det være å forårsake en deformasjon.

Et faststoff har sine veldig nære molekyler, og når du prøver mer, ser det ut til at frastøtningskrefter hindrer oppgaven. Derfor sies det at faste stoffer er ukompresjon. I flytende molekyler er det mer plass, så dens komprimerbarhet er større, men likevel krever volumendringen vanligvis store krefter.

Så faste stoffer og væsker er knapt komprimerbare. En veldig stor trykkvariasjon vil være nødvendig for å oppnå en betydelig endring i den såkalte normale trykk- og temperaturforholdene. På den annen side blir gasser, ettersom de har veldig avstand molekyler, lett komprimert og dekomprimert.

[TOC]

Solid komprimerbarhet

Når et objekt for eksempel er nedsenket i en væske, utøver det press på objektet i alle retninger. På denne måten kan vi tenke at volumet til objektet vil avta, selv om dette i de fleste tilfeller ikke vil være nevneverdig.

Situasjonen kan sees i følgende figur:

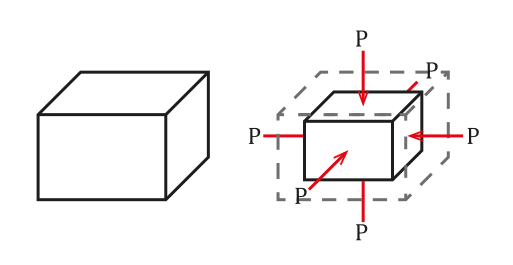Kraften som utøves av væsken på det nedsenkede objektet er vinkelrett på overflaten. Kilde: Wikimedia Commons.

Trykket er definert som kraft per enhet, som vil forårsake en volumendring ΔV proporsjonalt med det opprinnelige volumet til objekt V_enten. Denne volumendringen vil avhenge av egenskapene til det samme.

Hooke's lov uttaler at deformasjonen som et objekt opplever er proporsjonal med innsatsen som brukes på den:

Innsats ∝ Deformasjon

Den volumetriske deformasjonen som en kropp oppleves, blir kvantifisert med B den nødvendige proporsjonalitetskonstanten, som kalles som Volumetrisk modul av materialet:

B = -Seft/enhetlig deformasjon

Kan tjene deg: Termisk stråling: egenskaper, eksempler, applikasjoner

B = -ΔP/ (ΔV/ V_enten)

Som ΔV/V_enten Det er en dimensjonsløs mengde, fordi det er kvotienten mellom to bind, den volumetriske modulen har de samme trykkenhetene, som i det internasjonale systemet er Pascal (PA).

Det negative tegnet indikerer forventet reduksjon i volum, når objektet er komprimert nok, det vil si at trykket øker.

-Komprimerbarhet av et materiale

Den omvendte eller gjensidige verdien av den volumetriske modulen er kjent som komprimerbarhet Og det er betegnet med tekstene k. Derfor:

Her k Det er det negative av brøkvolumendringen på grunn av økning i trykk. Enhetene i det internasjonale systemet er det inverse av PA, det vil si m² /N.

Ligningen for B eller K hvis den er foretrukket, er gjeldende for både faste stoffer og væsker. Det volumetriske modulkonseptet brukes sjelden på gasser. Senere forklares en enkel modell for å kvantifisere nedgangen i volum som en ekte gass kan oppleve.

Lydens hastighet og komprimerbarhetsmodulen

En interessant applikasjon er lydhastigheten i et medium, som avhenger av komprimerbarhetsmodulen til det samme:

Der C er lydhastigheten, er B den volumetriske modulen og ρ er tettheten til mediet

Løste øvelser-eksempler

-Trening løst 1

En solid messingfære hvis volum er 0.8 m³ Den faller ned i havet til en dybde der det hydrostatiske trykket er 20 m større enn på overflaten. Hvilken endring vil oppleve volumet på sfæren? Det er kjent at messingkomprimerbarhetsmodulen er B = 35 000 MPa,

Løsning

1 m pa = 1 mega Pascal = 1. 10 ⁶ Pa

Trykkvariasjonen med hensyn til overflaten er dp = 20 x 10 ⁶ Pa. Bruker den gitte ligningen for B, har du:

B = -ΔP/ (ΔV/ V_enten)

Derfor:

Så:

ΔV = -5.71.10 ^-4 x 0.8 m³ = -4.57 x 10^-4 m³

Volumforskjellen kan ha et negativt tegn når sluttvolumet er mindre enn det opprinnelige volumet, derfor stemmer dette resultatet med alle forutsetningene vi har gjort så langt.

Komprimerbarhetsmodulen så høy, indikerer at det kreves en stor endring i trykket slik at objektet opplever en betydelig volumnedgang.

-Trening løst 2

Å sette øret mot togsporene er kjent når en av disse kjøretøyene nærmer seg i det fjerne. Hvor lang tid tar lyden når du reiser gjennom en stålbane hvis toget er 1 km unna?

Kan tjene deg: bevaring av det lineære momentumet: prinsipp, eksempler, øvelser.

Data

Ståltetthet = 7.8 x 10 ³ kg/m3

Stålkomprimerbarhetsmodul = 2.0 x 10 ^elleve Pa.

Løsning

Komprimerbarhet av væsker

Komprimerbarhetsmodul B beregnet ovenfor brukes også på væsker, selv om det vanligvis er nødvendig med en stor innsats for å gi en betydelig reduksjon i volum. Men væsker kan utvide eller trekke seg sammen når de varmer eller avkjøles, og også hvis de blir motløs eller presset på trykk.

For vann i standardtrykk og temperaturforhold (0 ºC og en trykkatmosfære omtrent eller 100 kPa) er den volumetriske modulen 2100 MPa. Det vil si omtrent 21000 ganger atmosfæretrykk.

Derfor, i de fleste applikasjoner, anses væsker vanligvis inkomprimerbare. Dette kan sees umiddelbart med numerisk anvendelse.

-Trening løst 3

Finn den brøkdekkende reduksjonen i vannvolum når det er utsatt for et trykk på 15 MPa.

Løsning

Komprimerbarhet i gasser

Gasser, som forklart ovenfor, fungerer litt annerledes.

Å vite hvilket volum de har n mol av en gitt gass når den holdes innesperret ved et trykk P og ved en temperatur T, Statligningen brukes. I tilstandsligningen for en ideell gass, der intermolekylære krefter ikke tas med i betraktningen, indikerer den enkleste modellen at:

P.V_ideell = n. R. T

Hvor r er konstanten av ideelle gasser.

Endringer i gassvolumet kan utføres ved konstant trykk eller ved konstant temperatur. For eksempel ved å holde temperaturen konstant, den isotermiske komprimerbarheten κ_T er:

I stedet for “Delta” -symbolet som ble brukt før de definerer konseptet for faste stoffer, for en gass er det beskrevet med derivat, i dette tilfellet delvis avledet med hensyn til P, og opprettholder konstant t.

Derfor B_T Den isotermiske komprimerbarhetsmodulen er:

 B_T = s

Og den adiabatiske BU -komprimerbarhetsmodulen B er også viktig_adiabatisk, Som det ikke er noen innkommende eller utgående varmestrømning.

B_adiabatisk = γP

Der γ er den adiabatiske koeffisienten. Med denne koeffisienten kan du beregne lydhastigheten i luften:

-Trening løst 4

Bruk den forrige ligningen, finn lydhastigheten i luften.

Data

Den adiabatiske luftkomprimerbarhetsmodulen er 1,42 × 10⁵ Pa

Lufttetthet er 1.225 kg/m³ (Ved atmosfærisk trykk og 15 ºC)

Løsning

Komprimerbarhetsfaktoren z

I stedet for å jobbe med komprimerbarhetsmodulen, som en enhetsendring av volum på grunn av trykkendring, er ekte gasskomprimerbarhetsfaktor, Et annet, men illustrerende konsept om hvordan ekte gass sammenligner med den ideelle gassen:

Kan tjene deg: bølgende teori om lys: forklaring, applikasjoner, eksempler

P . V_ekte = Z. R. T

Hvor z er konsistenes gasskomprimerbarhet, noe som avhenger av forholdene som det er, er vanligvis en funksjon av både P og temperatur T -trykket, og kan uttrykke seg som:

Z = f (p, t)

I tilfelle av en ideell gass z = 1. For reelle gasser øker Z -verdien nesten alltid med trykket og avtar med temperaturen.

Ved å øke trykket kolliderer gassformede molekyler oftere og de frastøtende kreftene mellom dem økes. Dette kan føre til en økning i volum i ekte gass, så z> 1.

På den annen side, for å senke presset, er molekylene fritt til å bevege seg og tiltrekningskreftene dominerer. I dette tilfellet, z < 1.

For det enkle tilfellet av 1 mol gass n = 1, hvis de samme trykk- og temperaturforholdene opprettholdes, oppnås ved å dele opp begrepet termin de tidligere ligningene:

Det konkluderes med at:

V_ekte = Z v_ideell

-Trening løst 5

Det er en reell gass ved 250 ºK og 15 atm trykk, som har et mololum 12 % lavere enn det beregnet med status som ideelle gasser. Hvis trykket og temperaturen forblir konstant, finn:

a) Komprimerbarhetsfaktoren.

b) Det molære volumet av ekte gass.

c) Hva slags krefter dominerer: attraktiv eller frastøtende?

Løsning

a) Hvis det virkelige volumet er 12 % lavere enn idealet, betyr det at:

V_ekte = 0.88 v_ideell

Derfor for 1 mol gass er komprimerbarhetsfaktoren:

Z = 0.88

b) Velge konstant av de ideelle gassene med de aktuelle enhetene for dataene som er gitt:

R = 0,082 l.atm/mol.K

Det molære volumet beregnes ved å rydde og erstatte verdier:

c) attraktive krefter dominerer, siden z er mindre enn 1.

Referanser

1. Atkins, p. 2008. Fysisk kjemi. Pan -American Medical Editorial. 10 - 15.
2. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6^th. Ed Prentice Hall. 242 - 243 og 314-15
3. Mott, r.  2006. Væskemekanikk. Pearson Education.13-14.
4. Rex, a. 2011. Fundamentals of Physics. Pearson Education. 242-243.
5. Tipler, s. (2006) Fysikk for vitenskap og teknologi. 5. utg. Volum 1. Redaksjon tilbake. 542.