Er det skalene trekanter med rett vinkel?

Det er mange skaleltrekanter med rett vinkel. Før du går videre om emnet, er det først nødvendig å kjenne de forskjellige trekantene som finnes. Trekantene er klassifisert av to klasser som er: deres indre vinkler og lengder på sidene.

Summen av de indre vinklene til en hvilken som helst trekant er alltid lik 180º. Men i henhold til interne vinkler er tiltak klassifisert som:

-Akutangel: Disse trekantene er slik at de tre vinklene deres er akutte, det vil si at de måler mindre enn 90 ° hver.

-Rektangel: De er de trekantene som har rett vinkel, det vil si en vinkel som måler 90 °, og derfor er de to andre vinklene akutte.

-Stump: De er trekantene som har en stump vinkel, det vil si en vinkel hvis mål er større enn 90 °.

Scalan trekanter med rett vinkel

Interessen for denne delen er å avgjøre om en scalene trekant kan ha rett vinkel.

Som sagt ovenfor, er en rett vinkel en vinkel hvis mål er 90º. Det er bare nødvendig å kjenne definisjonen av en scalene trekant, som avhenger av lengden på sidene av en trekant.

Klassifisering av trekanter i henhold til deres sider

I henhold til lengden på sidene deres, er trekantene klassifisert som:

-Likesid: De er alle disse trekantene slik at lengdene på de tre sider er de samme.

-Likebent: De er trekantene som har nøyaktig to sider av like lengde.

-Scalene: De er de trekantene som de tre sidene har forskjellige tiltak.

Formulering av et tilsvarende spørsmål

Et spørsmål som tilsvarer tittelen er “er det trekanter som har alle tre sider med forskjellige tiltak, og dette har en vinkel på 90 °?""

Svaret som sagt i begynnelsen er ja. Det er ikke veldig vanskelig å rettferdiggjøre dette svaret.

Hvis det er nøye observert, er ingen rektangel -trekant liksidig, dette kan rettferdiggjøres takket være Pythagoras teorem for rektangelets trekanter, som sier:

Gitt et rektangel -trekant at lengdene på kategoriene deres er "A" og "B", og lengden på hypotenusen er "C", må du C² = A²+B², som kan sees at lengden på hypotenusen " C "er alltid større enn lengden på hvert ben.

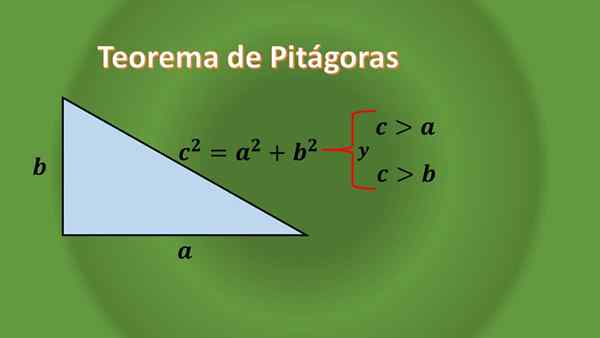
Som ingenting blir sagt om "A" og "B", innebærer dette at en riktig trekant kan være isosceles eller Scalene.

Deretter er det bare å velge hvilken som helst rektangel -trekant slik at bena har forskjellige tiltak, og dermed vil en scalene trekant som har rett vinkel blitt valgt.

Eksempler

-Hvis et rektangel -trekant regnes hvis ben har lengder på henholdsvis 3 og 4, kan det av Pythagoras teorem konkluderes med at hypotenusen vil ha en lengde på 5. Dette innebærer at trekanten er skalen og har rett vinkel.

-La ABC være et rektangel -trekant med målinger av måling 1 og 2. Da er lengden på hypotenusen √5, som konkluderer med at ABC er en Scalene Rectangle -trekant.

Ikke hver skala trekant har rett vinkel. Du kan vurdere en trekant som den av følgende figur, som er Scalene, men ingen av dens indre vinkler er rett.

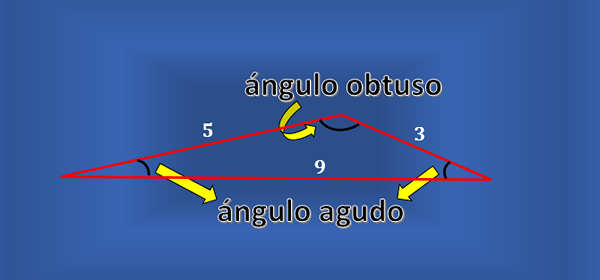I tillegg er ikke alle høyre trekant skalene. Hvis du vurderer en høyre trekant hvis ben måler begge 1, vil hypotenusen ha et mål på √2. Derfor er rektangelets trekant isosceles.