Komprimerbarhetsfaktor hvordan du beregner, eksempler og øvelser

Han Komprimerbarhetsfaktor z, o Komprimeringsfaktor for gasser er en dimensjonsløs verdi (uten enheter) som blir introdusert som en korreksjon i statuslikningen i Ideal Gases. På denne måten ligner den matematiske modellen den observerte oppførselen til gass mer.

I den ideelle gassen er tilstandsligningen som angår variablene P (trykk), V (volum) og T (temperatur): P.V _ideell = n.R.T med n = antall føflekker og r = konstant av de ideelle gassene. Ved å legge korreksjon av z -komprimerende faktor, blir denne ligningen transformert til:

P.V = z.n.R.T

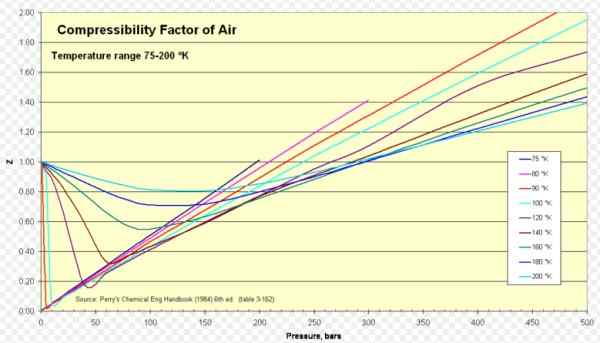
Figur 1. Luftkomprimerbarhetsfaktor. Kilde: Wikimedia Commons. https: // last opp.Wikimedia.org/wikipedia/commons/8/84/compressibility_factor_of_air_75-200_k.Png.

[TOC]

Hvordan beregne komprimerbarhetsfaktor?

Tatt i betraktning at molvolumet er V_kul = V/n, Du har det virkelige molære volumet:

P . V_ekte = Z. R. T → z = pv _ekte/Rt

Siden z -komprimerbarhetsfaktoren avhenger av gassforhold, uttrykkes den som en funksjon av trykk og temperatur:

Z = z (p, t)

Sammenlignet de to første ligningene, bemerkes det at hvis antallet mol n er lik 1, er molvolumet til en reell gass relatert til den for den ideelle gassen gjennom:

V_ekte / V_ideell = Z → v _ekte = Z v_ideell

Når trykket overstiger de 3 atmosfærene, slutter de fleste gassene seg som ideelle gasser og det virkelige volumet skiller seg betydelig fra idealet.

Dette realiserte i hans eksperimenter nederlandske fysiker Johannes van der Waals (1837-1923), noe som førte til at han skapte en modell som bedre justerte seg til de praktiske resultatene enn ligningen av ideelle gasser: tilstandsligningen til van der Waals.

Kan tjene deg: natriumoksalat (Na2C2O4): Struktur, egenskaper, bruksområder, risiko

Eksempler

I følge ligningen P.V_ekte= Z.n.Rt, For en ideell gass, z = 1. Imidlertid, i reelle gasser, ved å øke trykket gjør verdien av z. Dette er fornuftig fordi ved større trykkgassmolekyler har flere muligheter til å kollidere, derfor øker frastøtningskreftene og dermed volumet.

På den annen side til lavere trykk beveger molekylene seg med større frihet og frastøtningskreftene reduseres. Derfor forventes det et lavere volum. Når det gjelder temperaturen, når den øker, reduseres Z.

Som van der Waals observerte, i nærheten av det såkalte kritiske punktet, er gassatferd veldig avledet fra en ideell gass.

Det kritiske punktet (t_c, P_c) av ethvert stoff er trykk- og temperaturverdiene som bestemmer deres oppførsel før en faseendring:

-T_c Det er temperaturen over som den aktuelle gassen ikke er flytende.

-P_c  Det er det minste trykket som kreves for å flytende gassen ved temperatur t_c

Hver gass har sitt eget kritiske punkt, men definerer temperaturen og reduserte trykket t_r Og s_r følgende:

P_r = P / P_c

V_r = Volum_c

T_r = T /t_c

Det observeres at en gass innesperret med identisk V_r og T_r utøve det samme presset P_r. Av denne grunn, hvis z er grafisk avhengig av P_r til det samme T_r, Hvert punkt i den kurven er det samme for enhver gass. Dette kalles Prinsippet om tilsvarende stater.

Komprimerbarhetsfaktoren i ideelle gasser, luft, hydrogen og vann

Nedenfor er en komprimerbarhetskurve for forskjellige gasser ved forskjellige reduserte temperaturer. Deretter noen eksempler på Z for noen gasser og en prosedyre for å finne Z ved å bruke kurven.

Kan tjene deg: hydrogen: historie, struktur, egenskaper og bruk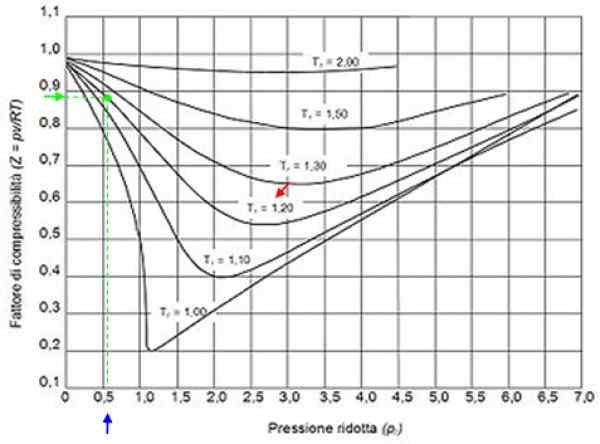Figur 2. Grafisk faktor grafikk for gasser i henhold til reduksjonstrykk. Kilde: Wikimedia Commons.

Ideelle gasser

De ideelle gassene har z = 1, som forklart i begynnelsen.

Luft

For luft z er omtrent 1 i et omfattende spekter av temperaturer og trykk (se figur 1), der den ideelle gassmodellen gir veldig gode resultater.

Hydrogen

Z> 1 for alle trykk.

Vann

For å finne Z av vannet er det nødvendig med verdiene til det kritiske punktet. Det kritiske punktet med vann er: P_c = 22.09 MPa og t_c= 374.14 ° C (647.3 k). Igjen er det nødvendig å ta hensyn til at Z -komprimerbarhetsfaktoren avhenger av temperaturen og trykket.

Anta for eksempel at du vil finne Z fra vannet ved 500 ºC og 12 MPa. Da er den første å beregne den reduserte temperaturen, som Celsius -grader må sendes til Kelvin: 50 ºC = 773 K:

T_r = 773/647.3 = 1.2

P_r = 12/22.09 = 0.54

Med disse verdiene lokaliserer vi i grafen til figuren kurven som tilsvarer t_r = 1.2, angitt med en rød pil. Så ser vi i den horisontale aksen verdien av P_r Nærmere 0.54, merket i blått. Nå tegner vi en vertikal til vi avskjærer T -kurven_r = 1.2 Og til slutt blir det projisert fra det tidspunktet til den vertikale aksen, der vi leser omtrentlig verdi av z = 0.89.

Løste øvelser

Oppgave 1

Det er en gassprøve ved en temperatur på 350 K og et trykk på 12 atmosfærer, med et molvolum 12 % høyere enn det som er forutsagt av Ideal Gases -loven. Regne ut:

a) z komprimeringsfaktor.

b) Molar volum av gass.

Kan tjene deg: irreversibel reaksjon: Kjennetegn og eksempler

c) I henhold til resultatene ovenfor, indikerer hvilke som er de dominerende kreftene i denne gassprøven.

Data: r = 0,082 l.atm/mol.K

Løsning på

Å vite at v _ekte  er 12 % høyere enn V_ideell :

V_ekte  = 1.12V_ideell

Z = v _ekte / V_ideell = 1.12

Løsning b

P . V_ekte = Z. R. T → V_ekte = (1.12 x 0.082 x 350 /12) l /mol = 2.14 l/mol.

Løsning c

Frastøtningskreftene er de som dominerer, siden volumet av prøven økte.

Oppgave 2

Det er 10 mol etan innesperret i et volum på 4.86 l a 27 ºC. Finn trykket utøvd av etan fra:

a) Den ideelle gassmodellen

b) Van der Waals -ligningen

c) Finn kompresjonsfaktoren fra de tidligere resultatene.

Data for etan

Van der Waals koeffisienter:

A = 5.489 DM⁶. ATM . mol^-2  og b = 0.06380 DM³. mol^-1.

Kritisk trykk: 49 atm. Kritisk temperatur: 305 K

Løsning på

Temperaturen føres til Kelvin: 27 ºC = 27 +273 K = 300 K, husk også at 1 liter = 1 l = 1 DM³.

Deretter erstattes dataene som er gitt i den ideelle gassligningen:

P.V = n.R.T → P = (10 x 0,082 x 300/4.86 l) ATM = 50.6 atm

Løsning b

Van der Waals State ligning er:

Hvor a og b er koeffisientene gitt av uttalelsen. Når du rydder P:

Løsning c

Vi beregner redusert trykk og temperatur:

P_r = 35.2/49 = 0.72

T_r = 300 /305 = 0.98 ≈ 1

Med disse verdiene søkes verdien av z i grafen i figur 2, og finner ut at z er omtrent 0.7.

 Referanser

1. Atkins, p. 1999. Fysisk kjemi. Omega -utgaver.
2. Cengel, og. 2012. Termodynamikk. 7^ma Utgave. McGraw Hill.
3. Engel, t. 2007. Introduksjon til fysikkjemi: termodynamikk. Pearson.
4. Levine, i. 2014. Prinsipper for fysikk-kjemi. 6. Utgave. McGraw Hill.
5. Wikipedia. Komprimerbarhetsfaktor. Hentet fra: i.Wikipedia.org.