Fraksjoner tilsvarer 3/4

De Fraksjoner tilsvarer 3/4 De er de der, ved å dele telleren mellom nevneren, resulterer det i desimaltallet 0.75.

Det er alltid mulig. Hvis resultatet av denne operasjonen er lik 0.75, tilsvarer brøkdelen 3/4, for eksempel brøkdel 6/8:

Fraksjon 6/8 tilsvarer ¾, siden ved å dele teller mellom nevneren i begge tilfeller 0 oppnås.75. Kilde: f. Zapata.

Nå ble brøkdel 6/8 oppnådd ved å multiplisere både telleren og ¾ nevneren. Ved samtidig å multiplisere telleren og denominatoren med samme mengde, endres ikke desimalverdien av en gitt brøkdel, men gjør det mulig å oppnå brøk som tilsvarer en gitt.

En annen måte å finne en brøkdel som tilsvarer en annen, ville være å dele teller og nevner med samme beløp. I tilfelle av ¾ er det imidlertid ikke mulig å finne et slikt tall som deler samtidig til 3 og 4, og resultatet er heltall. Dette er fordi 3 og 4 er søskenbarn med hverandre, så de har ikke vanlige delinger.

Når telleren og nevneren av en brøk er primtall med hverandre, sies det at brøkdelen er irreducible. Derfor er ¾ irreducible.

Måter å finne en brøkdel som tilsvarer en annen

Det er to veldig enkle måter å finne en brøkdel som tilsvarer en annen gitt brøkdel: den første er ved reduksjon og den andre ved forsterkning.

Reduksjon og forsterkning av brøk

Reduksjon

Denne prosedyren består av å finne et tall som er divisor for både telleren og nevneren. Når den er funnet, er både teller og nevner delt med denne verdien og oppnådde umiddelbart en brøkdel som tilsvarer originalen. Det er bekreftet at det dermed gjør tellerforholdet mellom nevner og sammenligning.

Kan tjene deg: matematiske funksjoner

Når den irreducible brøkdelen av en annen. Den således oppnådde brøkdelen er irreducible.

Fraksjonen ¾ er irreducible, som nevnt før, for å være 3 og 4 søskenbarn med hverandre, men følgende metode tillater uendelige brøkdeler som tilsvarer ¾.

Forsterkning

For å forsterke en gitt brøkdel, må telleren og denominatoren multipliseres med samme mengde, uansett om det er et positivt eller negativt tall. For eksempel ble fraksjon 6/8 oppnådd ved å forsterke ¾ ved faktor 2:

Selv om brøk har en annen teller og nevner, er begge de samme.

Legg merke til følgende figur, som inneholder to identiske sirkler, delt inn i like store deler, selv om den er av forskjellig størrelse. Områdene nøye har områdene i grønt og lilla samme tiltak, men det grønne området har blitt delt inn i 3 deler, av de 4 totalt som utgjør sirkelen til venstre. På den annen side ble sirkelen til høyre delt inn i 8 like deler, og det lilla området tilsvarer 6 av dem.

På denne måten kan du tegne at ¾ tilsvarer 6/8, siden begge brøkene representerer samme mengde.

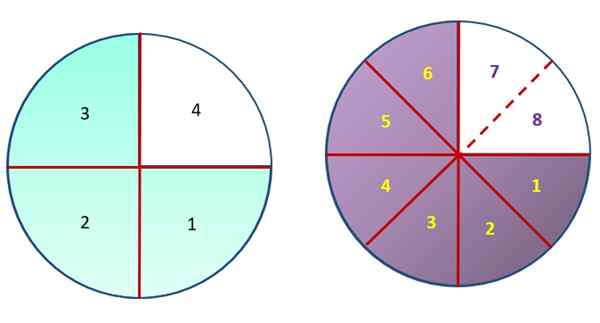Fraksjoner ¾ og 6/8 representerer det samme området i begge sirkler. Kilde: f. Zapata.

Generelt, hvis brøkdelen multipliseres ¾ med tall n, oppnås så mange fraksjoner som tilsvarer den som du vil:

Det er viktig å merke seg at N aldri kan være lik 0, siden divisjonen med 0 ikke er definert. Ingen brøk kan ha 0 i nevneren din.

Hvordan vite om en brøk tilsvarer 3/4?

Som forklart i begynnelsen, er en måte å vite om en brøkdel tilsvarer ¾ å gjøre kvotienten mellom telleren og nevneren. Hvis det er 0.75, tilsvarer brøkdelen ¾, men det er et par metoder å vite, som ikke krever inndeling direkte:

Det kan tjene deg: Vektede medier: Hvordan det beregnes, eksempler og øvelser

Metode 1

Anta at brøkdel A/B, og du vil vite om det tilsvarer ¾, det vil si om det er sant at:

For å være ekvivalent, må produkt 4 være lik produkt 3B:

4a = 3b

Metode 2

Hvis brøkdel A/B tilsvarer ¾, og deler A og B med sin maksimale vanlige MCD -divisor, må resultatet være ¾.

For å avklare bruken av disse metodene, se følgende eksempler.

Eksempler

Eksempel 1

Bestem om fraksjon 150/200 tilsvarer ¾:

Etter metode 1

I dette tilfellet A = 150 og B = 200, må det oppfylles at:

4a = 3b

• 4 × 150 = 600
• 3 × 200 = 600

Det er konkludert med at 150 /200 tilsvarer ¾.

Etter metode 2

Den maksimale vanlige divisoren på 150 og 300 deler dem begge. Begge mengder dekomponerer i sine viktigste faktorer, og deretter blir vanlige faktorer med deres minste eksponent multiplisert:

• 150 = 2 × 5² × 3
• 200 = 2³ × 5²

2 og 5 er vanlige, de multipliserer den minste kraften de vises med:

MCD (150, 200) = 2 × 5² = 2 × 25 = 50

Nå fortsetter vi å dele:

Løste øvelser

Oppgave 1

Skriv etter forsterkning Fem brøk som tilsvarer ¾, multipliserer teller og nevner hver gang med følgende hele tall:

a) 3, b) 5, c) (-2), d) 10 og e) 20

Løsning på

Løsning b

Løsning c

Merk at det ikke er noen forskjell ved å forsterke brøkdelen med 2 eller -2, siden i henhold til tegnregelen er kvotienten som er indikert mellom to negative mengder positivt.

Løsning d

Løsning e

Merk at denne brøkdelen er den samme som oppnådd ved å forsterke med 2 fraksjonen oppnådd ovenfor:

Oppgave 2

Kontroller om følgende brøk tilsvarer ¾:

Det kan tjene deg: Rektangulære koordinater: Eksempler og øvelser løst

a) 18/24; b) 21/28; c) 24/32; d) 27/38; e) 33/44

Løsning på

Bruke metode 1 beskrevet ovenfor:

4a = 3b

For brøkdel 18/24 må du = 18 og b = 24, da:

• 4 × 18 = 72
• 3 × 24 = 72

Derfor er 18/24 og 3/4 likeverdige.

Løsning b

I henhold til metode 2 må vi finne den maksimale vanlige divisoren (MCD) på 21 og 28, deretter dele både med resultatet, og hvis 3/4 -fraksjonen oppnås, er de likeverdige:

21 = 3 × 7
28 = 4 × 7 = 2²× 7

Den vanlige faktoren er 7, derfor MCD (21,28) = 7, deretter:

Løsning c

For denne øvelsen blir det sjekket om kvotienten mellom 24 og 32 er 0 0.75:

24 ÷ 32 = 0.75

Da tilsvarer 24/32 3/4.

Løsning d

I brøkdel 27/38 observeres det at 38 ikke er et multiplum av 4, derfor tilsvarer det ikke 3/4. Uansett blir forholdet mellom 27 og 38 utført:

27 ÷ 38 = 0.710526

Hvorav det konkluderes med at 27/38 ikke tilsvarer 3/4.

Løsning e

Det er lett å se at fraksjon 33/44 oppnås ved å multiplisere telleren og nevneren på 3/4 med 11, som dette:

Derfor er de likeverdige.