Faraday formel lov, enheter, eksperimenter, trening,

De Faraday Law I elektromagnetisme fastslår det at en endring av magnetfeltstrømmen er i stand til å indusere en elektrisk strøm i en lukket krets.

I 1831 opplevde den engelske fysikeren Michael Faraday å bevege sjåfører innenfor et magnetfelt og også varierende magnetfelt som krysset faste drivere.

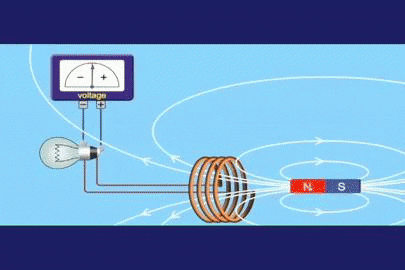Figur 1. Faraday Induction Experiment

Faraday innså at hvis han varierer magnetfeltet i tid, var han i stand til å etablere en spenning proporsjonal med nevnte variasjon. Hvis ε er den induserte elektromotoriske spenningen eller kraften (indusert FEM) og φ er magnetfeltstrømmen, i matematisk form kan den uttrykkes:

| ε | = Δφ/Δt

Hvor symbolet Δ indikerer variasjon av mengden og stengene i FEM indikerer den absolutte verdien av dette. Siden det er en lukket krets, kan strømmen sirkulere i en eller annen retning.

Magnetfluksen, produsert av et magnetfelt gjennom en overflate, kan variere på forskjellige måter, for eksempel:

-Flytte en stangmagnet gjennom en sirkulær spiral.

-Øker eller reduserer intensiteten til magnetfeltet som krysser sløyfen.

-Forlater feltet fikset, men ved en eller annen mekanisme endre løkkenes område.

-Kombinere metodene ovenfor.

Figur 2. Den engelske fysikeren Michael Faraday (1791-1867).

[TOC]

Formler og enheter

Anta at det er en lukket krets med område A, for eksempel en sirkulær spiral eller en opprør lik figur 1, og at det er en magnet som produserer et magnetfelt B.

Magnetfeltstrømmen φ er en skalær mengde som refererer til mengden feltlinjer som krysser området a. I figur 1 er de hvite linjene som etterlater den nordlige polen til magneten og kommer tilbake i sør.

Kan tjene deg: Brayton Cycle: Prosess, effektivitet, applikasjoner, øvelser

Intensiteten til feltet vil være proporsjonal med antall linjer per enhet, så vi kan se at det ved polene er veldig intens. Men vi kan ha et veldig intenst felt som ikke produserer flyt i løkken, som vi kan oppnå ved å endre orienteringen til dette (eller magneten).

For å ta hensyn til orienteringsfaktoren, er magnetfeltstrømmen definert som skalarproduktet mellom B og n, å være n Den normale enhetsvektoren til overflaten av spasen og som indikerer dens orientering:

Φ = B•n A = ba.cosθ

Hvor θ er vinkelen mellom B og n. Hvis for eksempel B og n De er vinkelrett, magnetfeltstrømmen er ugyldig, for i så fall er feltet tangent til spaseplanet og ikke kan krysse overflaten.

I stedet B og n De er parallelle, det betyr at feltet er vinkelrett på spira -planet og linjene går gjennom det maksimalt.

Den internasjonale systemenheten for F er Weber (W), der 1 W = 1 t.m² (lyder "Tesla per kvadratmeter").

Lenz Law 

I figur 1 kan vi se at polariteten til spenningen endres når magneten beveger seg. Polaritet er etablert av Lenzs lov, som sier at den induserte spenningen må motsette variasjonen som produserer den.

Hvis for eksempel magnetisk fluks produsert av magneten øker, oppretter sjåføren en strøm som sirkulerer og skaper sin egen flyt, noe som motsetter seg denne økningen.

Hvis, tvert imot, strømmen skapt av magneten avtar, sirkulerer den induserte strømmen på en slik måte at dens egen strøm motvirker sagt reduksjon.

Kan tjene deg: termometriske skalaer

For å ta hensyn til dette fenomenet, blir et negativt tegn på Faradays lov satt før, og det er ikke lenger nødvendig å plassere de absolutte verdibinjene:

ε = -Δφ/Δt

Dette er Faraday-Lenzs lov. Hvis strømningsvariasjonen er uendelig, erstattes deltas av differensialer:

ε = -dφ/dt

Den forrige ligningen er gyldig for en loop. Men hvis vi har en spinnspole, er resultatet mye bedre, fordi FEM multipliserer n ganger:

ε = - n (dφ/dt)

Faraday eksperimenter

For å produsere strømmen som lyser lyspæren, må det være en relativ bevegelse mellom magneten og spiralen. Dette er en av måtene flyten kan variere på, for på denne måten endrer intensiteten på feltet som krysser sløyfen endres.

I det øyeblikket magnetbevegelsen opphører, går pæren ut, selv om magneten fortsatt er i spasen. Det som trengs for å sirkulere strømmen til lyspæren er at feltstrømmen varierer.

Når magnetfeltet varierer over tid, kan vi uttrykke det som:

B = B (T).

Ved å holde spasens område konstant og la det fikses i en konstant vinkel, som i tilfelle av figuren er 0º, deretter:

 For sløyfen i figur 1 (cos 0º = 1):

Variabel areal spase

Hvis du kan endre spaseområdet, etterlate orienteringen å fikse og sette den midt i et konstant felt, er den induserte FEM gitt av:

En måte å oppnå dette på er å legge en stolpe som glir på en ledende skinne med en viss hastighet, som vist i følgende figur.

Kan tjene deg: ío (satellitt) Figur 3. Glidende generator. Kilde: Serway, R. Fysikk for vitenskap og ingeniørfag.

Stangen og skinnen, pluss en pære eller en motstand forbundet med førertråd, danner en lukket krets i form av rektangulær spase.

Når du skyver baren, lengden x øker eller avtar, og med det endres området for sløyfen, noe som er nok til å skape en variabel strømning.

Variasjon av magnetisk fluks etter rotasjon

Som vi sa før, hvis vinkelen mellom B Og det normale av sløyfen er variert, feltstrømmen endres i henhold til:

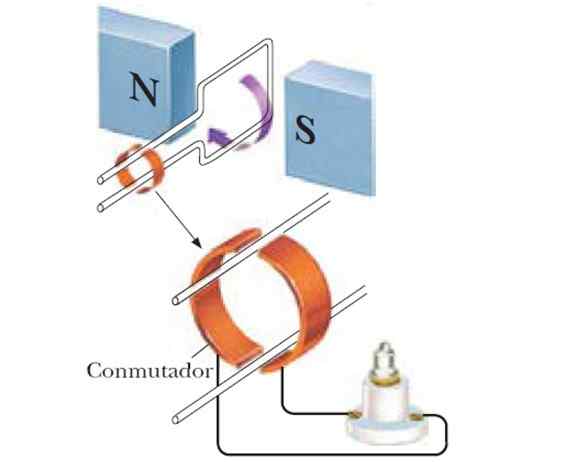Figur 4. Hvis sløyfen roteres mellom polene til en magnet, oppnås en sinusformet generator. Kilde: f. Zapata.

En sinusformet generator oppnås således, og hvis et enkelt antall spoler brukes, er den induserte FEM større:

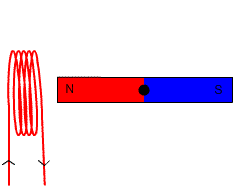Figur 5. I denne generatoren roteres magneten for å indusere strømmen i spolen. Kilde: Wikimedia Commons.

Trening løst

En sirkulær spole med N -runder og radio R, svinger vinkuløst ω midt i et magnetisk størrelsesfelt b. Finn et uttrykk for det maksimale induserte FEM i spolen.

Løsning

Uttrykket for FEM indusert av rotasjon blir påført når spolen har N -runder, og vet at:

-Spoleområdet er A = πr²

-Vinkelen θ varierer avhengig av tid som θ = ωt

Det er viktig å ta hensyn til at θ = ωt først erstattes i Faradays lov og deretter Det er avledet fra tid:

ε = -nba (cos θ) '= -nb (πr²).[cos (ωt)] '= nbω (πr²) Sen (ωt)

Siden den maksimale FEM blir bedt om, skjer dette når Sen ωt = 1, så endelig:

ε_Maks = Nbω (πr²)

Referanser

1. Figueroa, d. 2005. Serier: Fysikk for vitenskap og ingeniørfag. Volum 6. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysikk. Andre utgave. McGraw Hill.
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed. Prentice Hall.
4. Resnick, r. 1999. Fysisk. Vol. 2. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V.
5. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 2.