Matte

Bestilt par

Bestilt par

Hva er et ordnet par?

Et ordnet par eller Duo Det er et sett med to elementer som er skrevet i henhold til ordren som er etablert av et visst kriterium. Nevnte kriterier spesifiserer hvilke av de to elementene som går først, og hvilken som går etter.

Det bestilte paret er betegnet som (x, y), der "x" er det første elementet i paret og "y" er det andre, også kalt Komponenter. Generelt (x, y) er det ikke det samme ryddige dreiemomentet (y, x). Og i tillegg til rekkefølgen, er et annet viktig kjennetegn ved de bestilte parene likhet: to bestilte par (a, b) og (c, d) er de samme bare hvis a = c og b = d.

Figur 1.- Takket være de ryddige parene vet valpen at beinene er begravet på stedene (3,1) og (-4,2), mens huset hans er i (0,0). Kilde: f. Zapata.

Eksempler på bestilte par ville være de som er sammensatt av alder og vekten til et matematikkstudenterkurs. Det bestilte paret (15, 62) tilsvarer en 15 -årig student, forskjellig fra det usannsynlige paret (62,15).

Konseptet med et ordnet dreiemoment er veldig viktig på forskjellige områder av matematikk, for eksempel det kartesiske planet, brøk, vektorer i planet, forhold og funksjoner. Et viktig aspekt er at elementene deres ikke nødvendigvis har numeriske, for eksempel kan de bestilles med:

  • Landlig by
  • Navn etternavn
  • Kone Mann

Og mange andre kombinasjoner.

Eksempler på bestilte par

Brøk

En brøk er representert som kvotienten til to P/Q -heltall, for eksempel brøkdelen ½, som tilsvarer desimaltallet 0.5.

Imidlertid er denne brøkdelen ikke den eneste som representerer desimal 0.5, så gjør følgende:

2/4; 3/6; (-2)/(-4); 20/40; (-1)/(-2) ..

På denne måten kan enhver brøkdel representeres som et ordnet par (P, Q), der P og Q er hel, med P som okkuperer plasseringen til telleren og Q som denominatoren. Det er en viktig begrensning og at Q (nevneren) må være annerledes enn 0, siden brøkene i P/0 -skjemaet ikke er definert.

Kan tjene deg: endelig sett: egenskaper, eksempler, løste øvelser

Og en annen viktig betingelse er at to brøk A/B og C/D er like så lange som det er oppfylt at:

A ∙ d = b ∙ c

Funksjoner og grafene

En funksjon kan uttrykkes som et sett med ryddige par. For eksempel ved å tegne en funksjon i det kartesiske planet, tildeles det første elementet plasseringen av den uavhengige variabelen, mens den andre tildeles den avhengige variabelen. Dette er et ordnet par.

For y = f (x) -funksjonen kan det ryddige dreiemomentet uttrykkes som [x, f (x)]]. Tenk for eksempel startsettet:

A = 1, 2, 3, 4

I dette settet er det de første komponentene i et ordnet par i henhold til y = x -funksjonen2. Settet med de andre komponentene er:

B = 1, 4, 9, 16

Og de bestilte parene er dannet er:

(1,1); (2,4); (3, 9); (4; 16)

Hensyn.

Vektorer i planet

Vektorer kan være representert i det kartesiske planet ved bestilte par, der det første elementet representerer den horisontale komponenten "x" og den andre den vertikale komponenten "y". For å skille vektorene fra punktene i planet, er de betegnet med dristige bokstaver og firkantede parenteser brukes i stedet for parentesene, som dette:

v =

For eksempel vektoren v = har en horisontal komponent lik 4 og vertikal komponent lik 7. Grafen er:

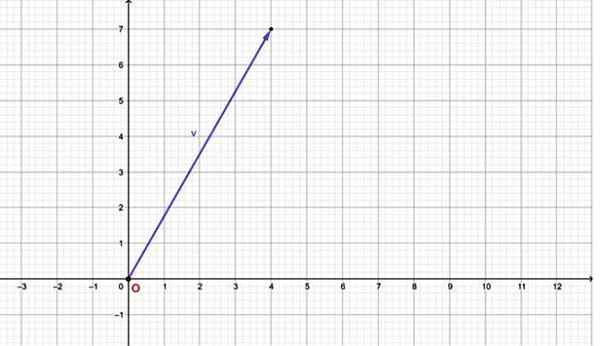Figur 2.- En planvektor kan uttrykkes gjennom et ordnet par. Kilde: f. Zapata.

Merk at denne vektoren har sin opprinnelse sammenfallende med opprinnelsen til koordinatsystemet (0.0). Hvis vektoren har sin opprinnelse på et hvilket som helst annet punkt, kan det også uttrykkes i form av et ordnet dreiemoment gjennom et ordnet par, for å gjøre det, se følgende seksjoner.

Kan tjene deg: hierarki av operasjoner

Bestilte Pares -operasjoner

Addisjon

La målene (a, b) og (c, d) være par (d). Et nytt dreiemoment oppnås ved hjelp av summen i henhold til:

(a, b)+(c, d) = (a+c, b+d)

Nøytralt element

Det nøytrale elementet i tilsetningen av bestilte par er dreiemomentet (0,0), siden når det legger til det bestilte paret (a, b), er summen sistnevnte:

(a, b) + (0,0) = (a, b)

Sum av det motsatte

Ved å legge til et ordnet par (a, b) med det motsatte (-a, -b) oppnås det ordnede dreiemomentet (0,0):

(a, b) + (-a, -b) = (0,0)

Kommutativitet

Bestillingen på tilleggene endrer ikke summen:

(a, b) + (c, d) = (c, d) + (a, b)

Assosiativitet

Resultatet av å legge til tre bestilte par endres ikke når det er gruppert for å utføre operasjonen:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]

Subtraksjon av bestilte par

La målene (a, b) og (c, d) være, subtraksjonen utføres som følger:

(A, B)-(C, D) = (A-C, B-D)

Produkt

I produktet er det to alternativer: i) multiplisere et dreiemoment bestilt med en konstant og ii) multiplisere to (eller flere) budskap.

Multiplikasjon med en konstant

La K være et konstant og det ordnede dreiemomentet (a, b), produktet mellom konstanten og dreiemomentet er:

K ∙ (a, b) = (k ∙ a, k ∙ b)

Multiplikasjon av bestilte par

Produktet mellom de bestilte parene (a, b) og (c, d) utføres som følger:

(A, B) X (C, D) = (AC - BD, BC+AD)

Nøytralt element

Det nøytrale elementet i multiplikasjon er (1.0), siden ved å multiplisere ethvert dreiemoment bestilt med dette, etter multiplikasjonsregelen beskrevet ovenfor, er det opprinnelige dreiemomentet:

(a, b) x (1.0) = (a - 0, b + 0) = (a, b)

Kan tjene deg: Multiplikativ omvendt: Forklaring, eksempler, løste øvelser

Assosiativitet

Ettersom rekkefølgen på faktorene ikke endrer produktet, kan det grupperes på forskjellige måter å multiplisere tre eller flere ryddige par, og resultatet er det samme:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]

Løste øvelser

Oppgave 1

Du har bestilt par (x2, X-2) = (16, 2). Som er verdien av x?

Løsning

Bruk av likestilling av bestilte par oppnås først:

x2 = 16 ⇒ x1 = 4, x2 = -4

Å vite hvilke av de to verdiene som velger, bruk av:

X-2 = 2

x = 2 + 2 = 4

Derfor er den forespurte verdien av x 4.

Oppgave 2

Uttrykke som et ordnet parvektoren som går fra punkt (1, 3) til punktet (7, 11) og representerer den grafisk.

Løsning

Være v Vektoren søkte. For å bestemme det ordnede paret som representerer det, og som inneholder det. Så:

v = =

Vektoren er deretter representert v som den som går fra (1.3) til (7, 11) og utstyret v hvis opprinnelse er festet til opprinnelsen til koordinatsystemet (0,0). Som du ser har de samme retning og mening.

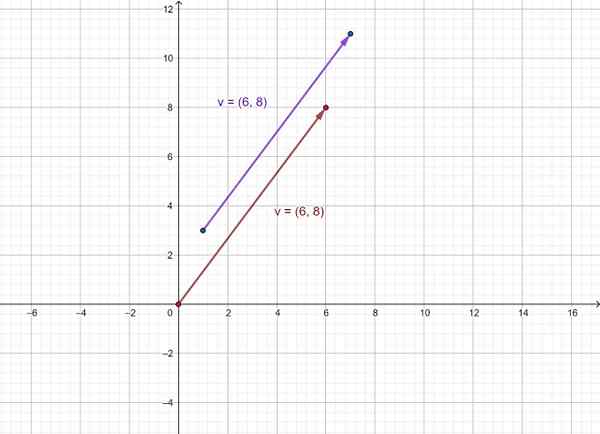Figur 3. Representasjon av en vektor som et ordnet par. Kilde: f. Zapata.

Referanser

  1. Deepal. Bestilt par. Gjenopprettet fra: Deepai.org.
  2. Mathemovil. Kartesisk representasjon av en vektor av et ordnet par. Gjenopprettet fra: Matemovil.com.
  3. Varsity Tutorrs. Bestilt par. Hentet fra: Warsitytorm.com
  4. Priestri, Juan. Forhold og funksjoner. Fakultet for ingeniørfag. Institutt for matematikk. Buenos Aires 'University. Hentet fra: fag.fi.Uba.ar.
  5. University of Denver. Forhold. Gjenopprettet fra: Matematikk.Ucdenver.Edu.