Vekt (fysisk) beregning, enheter, eksempler, øvelser

Han vekt Det er kraften som jorden tiltrekker seg gjenstander til overflaten. Hver gang et objekt blir droppet, går dette til bakken, det er ikke i stand til å klatre på sine egne midler og heller ikke bli ugraktet halvveis, noe som er fordi jorden tiltrekker seg den.

Alle objekter tiltrekker seg alltid med hverandre, til og med de små, bare at størrelsen på kraften de gjør er proporsjonal med massen. Dette betyr at gjenstander med liten masse utøver liten styrke over andre, men himmellegemer som Jorden er i stand til å utøve en veldig stor kraft.

Jorden holder månen som kretser rundt den takket være denne tiltrekningskraften, som kalles Gravitasjonsattraksjon Når det gjelder gjenstander som er langt fra jordens overflate, og vekt Når gjenstander er nærme.

Dette følger at tyngdekraften ikke krever at objekter nødvendigvis er i kontakt med hverandre for å handle: det er derfor det sies at det er en handlingsavstand.

Gjenstandene har fortsatt vekt selv om de er i en viss høyde på bakken og jo mer massive, jo større er denne vekten.

Den store engelske forskeren Isaac Newton var den første som ga en forklaring om dette problemet, gjennom den universelle gravitasjonsloven som bærer navnet hans, og som siden den gang har tjent til å forstå hvordan gjenstander samhandler med masse med masse. Dette er veldig viktig, siden ethvert objekt på planeten har vekt.

[TOC]

Vektenheter

Det internasjonale enhetssystemet hvis vekten for vekt er Newton, Oppkalt til ære for Isaac Newton. Dette er enheten for å måle krefter av alle slag.

Newton, forkortet N, er definert som den nødvendige styrken for et masseobjekt på 1 kg å skaffe seg en 1m/s akselerasjon². Bortsett fra Newton, er det andre enheter med vanlig bruk, for eksempel følgende:

Kilogramstyrken

Han Kilogram-Force o kilopondio, forkortet kg-f eller kp, selv om det ofte kalles kg uten videre. Det er nødvendig å spesifisere plasseringen, siden gravitasjonsfeltet opplever variasjoner med høyde og breddegrad som sagt med høyde og breddegrad.

Når noen sier at det veier 45 kg, er det i virkeligheten at vekten deres er 45 kg-f, fordi kilo er enheten som er reservert for massen.

Kan tjene deg: Åpen krets

Ekvivalensen mellom kg-f og n er: 1 kg-f = 9.8 n

Pundkraften

De Vågen-Fuerza, Forkortet LB-F er også en kraftenhet som er analog med KG-F, siden det er kraften som jorden utøver på et objekt på 1 pund masse. Og som med KG-F, er det ikke noe problem med verdiene når du er på jorden, det vil si et objekt for massen av masse, veier 1 lb-f-f.

Ekvivalensen i LB-F og N er: 1 lb-f ≡ 4.44822 N.

Vektberegning og formel

Vekten av et objekt er proporsjonal med massen. En større masse, større vekt.

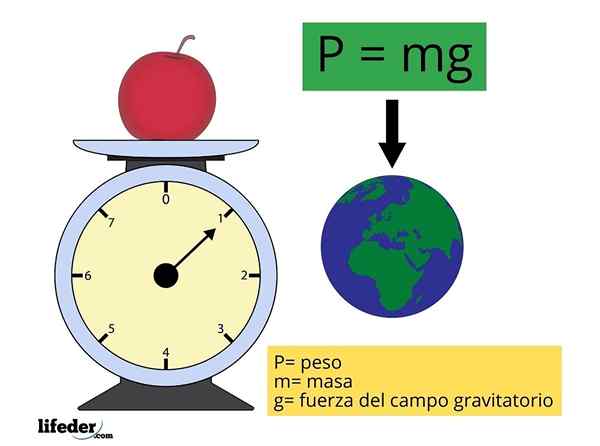
Formelen for å finne størrelsen på vekt P (eller også w, som noen ganger betegner, av "Vekt" På engelsk) er det veldig enkelt:

P = mg

Hvor m representerer massen til objektet og g Det er størrelsen på akselerasjonen av tyngdekraften (intensiteten til gravitasjonsfeltet eller alvorlighetsgraden), omtrent konstant og hvis verdi er tatt som 9.81 m/s² For de hyppigste beregningene.

Vekten er en vektor og å skille mellom en vektor og dens størrelse de dristige bokstavene brukes. På denne måten, når du snakker om P, forstås det at det er den numeriske verdien og når den er skrevet P Det vises til vektoren:

P = m ∙g

De g Med dristige tekster er det landets gravitasjonsfelt, det vil si innflytelsen som jorden utøver på det rommet som omgir det, uavhengig av om det er en annen kropp som oppfatter det eller ikke. Ethvert objekt med masse har sitt eget gravitasjonsfelt, enten det er lite eller stort.

Intensiteten til landets gravitasjonsfelt g Det er ikke helt konstant. Den har små variasjoner som hovedsakelig oppstår fordi jorden ikke er en perfekt sfære og også til lokal høyde- og tetthetsforskjeller. Men for de fleste applikasjoner, verdi 9.81 m/s² Det fungerer veldig bra.

Andre himmellegemer har sitt eget karakteristiske gravitasjonsfelt, derfor skiller akselerasjonen av tyngdekraften seg i henhold til planeten eller satellitten. Det samme objektet ville ha en annen vekt i hver enkelt, og derfor er ikke vekten en karakteristisk egenskap av ting, men av emnet generelt.

Vekten som en vektor

Vekten er en vektor og har derfor størrelse, retning og mening. I nærheten av jordoverflaten er vekten en vertikal vektor og retningen er alltid nede.

Generelt er den vertikale adressen utnevnt som akse og enten z, Og betydningen er tildelt tegn + eller tegn - for å skille det fra retningen opp. Valget avhenger av opprinnelsen til opprinnelsen. I det nedre bildet ble opprinnelsen valgt på det punktet som eplet faller fra:

Kan tjene deg: ideell gass: modell, oppførsel, eksempler Vekten er en vektor som er rettet vertikalt ned. Kilde: f. Zapata.

Enhetsvektoren J, En størrelsesvektor lik 1, brukes til å peke og skille vertikal retning. Når det gjelder denne vektoren, er vekten skrevet slik:

P = mg ( - J)

Hvor negativt tegn er tilordnet retningen.

Forskjeller mellom vekt, masse og volum

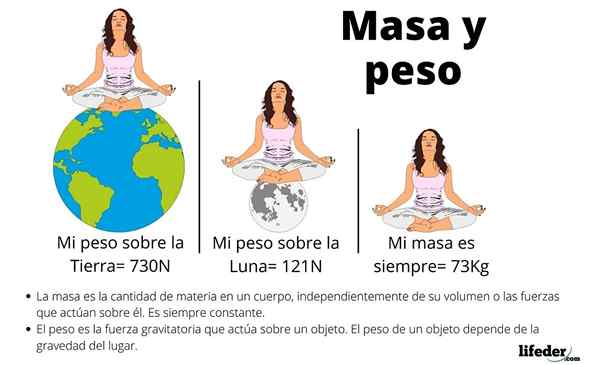
Ofte er disse tre konseptene forvirrede, men gjennomgår egenskapene til vekten, er det lett å skille den fra masse og volum.

For å starte, avhenger vekten av gravitasjonsfeltet til stedet der objektet er. For eksempel på jorden og på månen har det samme en annen vekt, selv om mengden atomer som utgjør den er konstant.

Massen er en skalær størrelse, relatert til mengden atomer som utgjør objektet og er bevist med motstanden som objektet må endre bevegelsen, en egenskap som heter treghet.

For sin del er volumet målet på plassen okkupert av et objekt, en annen skalær mengde. To objekter med like volum veier ikke det samme, for eksempel veier en jernkube mye mer enn en annen polystyren av de samme dimensjonene.

Oppsummert:

• Massen er relatert til mengden av materie som et legeme har.
• Vekten er kraften som jorden utøves på den massen, proporsjonal med den.
• Volum er plassen okkupert av materie.

Det skal bemerkes at å være skalare mengder, verken massen eller volumet har retning eller mening, men bare numerisk verdi og en tilstrekkelig enhet. På den annen side må vekten, som en vektor, alltid uttrykkes riktig påpeke størrelsen, enhet, retning og mening, som i forrige seksjon.

Eksempler på vekt

Alle gjenstander på jorden har vekt, du kan til og med "veie" gjenstander som ikke er på jorden, for eksempel andre planeter eller solen, selv om det selvfølgelig er det.

Ettersom vektområdet er veldig stort, brukes vitenskapelig notasjon (i krefter på 10) for å uttrykke noen som er veldig store eller veldig små:

-Solen: 1 989 × 10³⁰ kg-f

-Jupiter: 1.898 × ​​10²⁷ kg-f

-En mygg: 2.0 × 10^-5 N

-Babyer: 34.3 n

-Et barn: 353 n

-Voksen person: 65 kg-f

-En voksen elefant: 5.5 × 10³ kg-f

-Blå hval: 1.0 × 10⁶ N

Trening løst

En deigboks 20 kg hviler på et bord.

a) Finn vekten på boksen og normalkraften som bordet utøver på den.

Kan tjene deg: bevaring av det lineære momentumet: prinsipp, eksempler, øvelser.

b) ytterligere 10 kg boks er plassert på den første. Finn den normale som bordet øver på 20 kg -boksen og den normale som den utøver på den minste boksen.

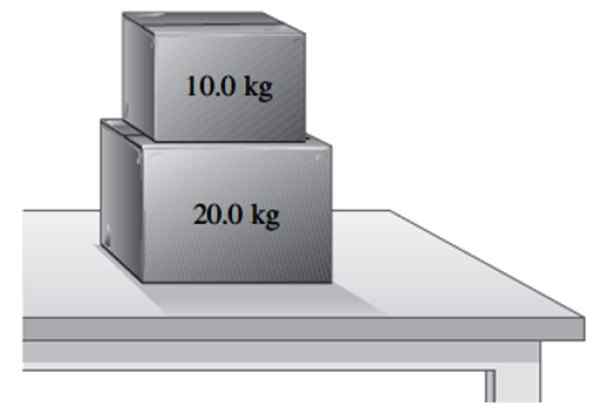To bokser som hviler på et bord. Kilde: f. Zapata.

Løsning på

Det er praktisk å lage et gratis kroppsdiagram på boksen, som består av å tegne kreftene som virker på den.

I denne situasjonen er det fortsatt den minste boksen på toppen, derfor er det bare to krefter: den første er vekten P som er trukket vertikalt nede, som indikert i de foregående seksjonene og deretter er det normalt N, som er den vinkelrett kraften som bordet utøver og forhindrer boksen i å falle.

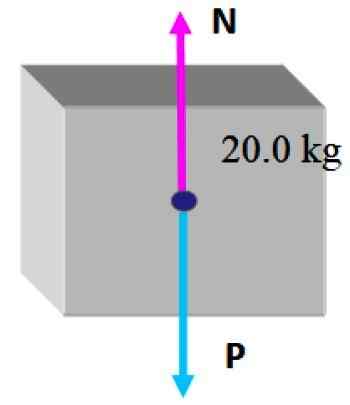
Siden boksen er i statisk likevekt under disse omstendighetene, er det rimelig å konkludere med at størrelsen på det normale er den samme som vekt, slik at den kan kompensere, derfor:

N = mg = 20.0 kg x 9.8 m/s² = 196 n; rettet vertikalt opp.

For sin del er vekten P = 196 N rettet vertikalt ned.

Løsning b

Nå er det laget nye gratis kroppsdiagrammer om begge objektene. For den store boksen endres ting litt, siden den lille boksen utøver styrke på den.

Kreftene er som følger: N og P De er henholdsvis den normale som bordet øvelser og vekten på boksen med 20.0 kg, som ikke endret seg. Og den nye styrken utøvd av den lille boksen er N₁, det normale på grunn av kontakt med den øvre ansiktet til den store boksen.

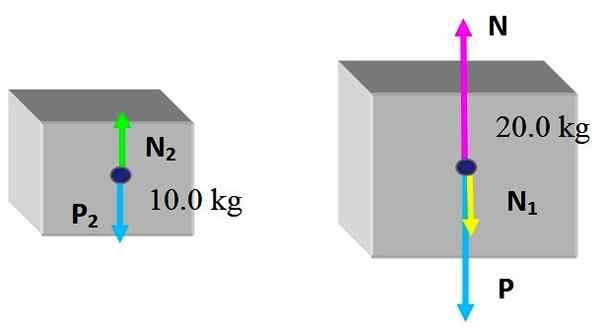
Når det gjelder den lille boksen, mottar den normalen N₂, utøvd av den øvre ansiktet til den store boksen og selvfølgelig dens vekt P₂. Siden boksene er statisk balanse:

N₂ - P₂ = 0

N - n₁ - P = 0

Fra den første ligningen må du n₂ = S₂ = 10 kg x 9.8 m/s² = 98 n. Ved lov om handling og reaksjon er størrelsen på kraften som den lille boksen mottar, den samme som den utøver på den store boksen, da:

N₂ = N₁ = 98 n

Fra den andre ligningen er det normale n som tabellen øver på den store boksen er fjernet, som igjen har den lille boksen på toppen:

N = n₁ + P = 98 n + 196 n = 294 n

Referanser

1. Figueroa, d. 2005. Serier: Fysikk for vitenskap og ingeniørfag. Volum 2. Dynamisk. Redigert av Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysikk. 2. Ed. McGraw Hill.
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1. Pearson.
5. Serway, r., Jewett, J. 2008. Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.
6. Thomas Griffith, w. 2007. Konseptuell fysikk. Mc Graw Hill.