Fysisk

Prinsippet om krefter overførbarhet

Prinsippet om krefter overførbarhet

Vi forklarer hva som er prinsippet om overførbarhet, med eksempler og øvelser løst

Hva er overførbarhetsprinsippet?

Han Overførbarhetsprinsipp Det gjelder faste gjenstander og bekrefter at en påført kraft på et eller annet punkt er tilsvarer en annen kraft av like stor størrelse og retning, så lenge nevnte kraft blir brukt på samme linje som inneholder den opprinnelige kraften.

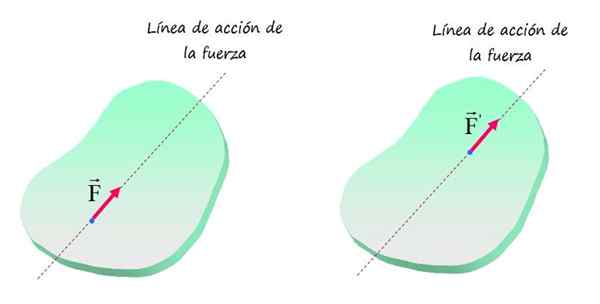
Derfor vil enhver kraft i samme størrelse og retning føre til samme effekt av translasjons- og rotasjonsbevegelse på objektet, forutsatt at dets anvendelsespunkt er plassert på samme linje, som vist i følgende figur.

I et stivt legeme blir ikke effekten av en kraft endret når anvendelsespunktet beveger seg langs sin handlingslinje. Kilde: f. Zapata.

Styrkene som er vist F og F'Det sies at de er tilsvarende krefter og den plutselige rette linjen som inneholder dem kalles Forta handlingslinje.

Overførbarhetsprinsippet er veldig nyttig, siden det tillater bekvemmelighet kreftene som virker på objektet, for å lette analysen.

Forklaring av Overførbarhetsprinsipp

Overførbarhetsprinsippet er basert på det faktum at to krefter F1 og F2 De er likeverdige, under forutsetning av at de har samme størrelse og samme retning.

I tillegg må de produsere det samme øyeblikket med hensyn til et hvilket.

Legg merke til at prinsippet bare gjelder på et stivt legeme, det vil si et objekt der de relative avstandene mellom delene deres ikke endres, fordi de indre kreftene som holder det i samhold er intense nok. Derfor endrer ikke objektet dens form, enten den ytre krefter virker på det eller ikke.

På den annen side, hvis objektet ikke er stivt, vil det å modifisere påføringspunktet for kreftene produsere variasjoner når det gjelder spenning eller kompresjon påført kroppen, noe som vil føre til endringer i den.

Antar selvfølgelig at en kropp er stiv. Imidlertid er det i mange tilfeller en utmerket tilnærming, hvis deformasjonen er liten nok til å bli ansett som foraktelig.

Begrensninger

Overførbarhetsprinsippet har som indikert en begrensning angående de interne effektene av skyting eller gliding av kreftene. I den følgende figuren vises et objekt, med kreftene F og F'Anvendt i forskjellige punkter med samme handlingslinje.

Kan tjene deg: Archimedes -prinsipp: Formel, demonstrasjon, applikasjoner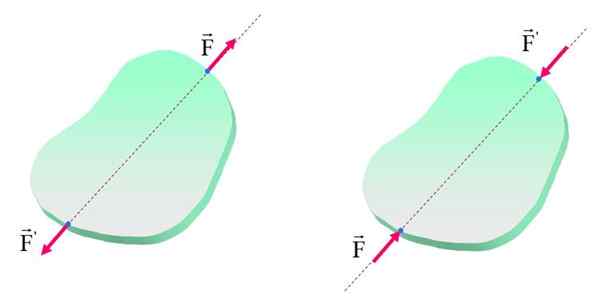Overførbarhetsprinsippet gjelder bare i stive kropper, siden modifisering av påføringspunktet for kreftene kan forårsake forskjellige effekter på deformerbare kropper. Kilde: f. Zapata.

Legg merke til at i begge figurer er kroppen (stiv eller ikke) i balanse, fordi kreftene har like stor størrelse og retning og motsatte sanser. I tillegg er kreftene, som sagt, på samme handlingslinje, men i venstre figur er effekten på kroppen spenning mens til høyre er effekten kompresjon.

Derfor, selv om kroppen forblir i ro, er de interne effektene forskjellige og blir patent hvis objektet ikke er helt stivt. Når det gjelder venstre, har styrkene en tendens til å utvide kroppen, mens de til høyre har en tendens til å forkorte det.

Eksempler av Overførbarhetsprinsipp

Eksempel 1

Anta at du har en tung bagasjerom på et horisontalt gulv. Effekten av å skyve den på venstre side er den samme som om den er flat. I dette tilfellet er bevegelsen av bagasjerommet på bakken den samme.

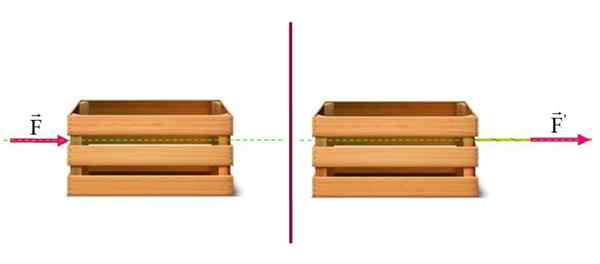Effekten av å skyve eller trekke skuffen på den horisontale overflaten er den samme: flytt den fra venstre mot høyre. Kilde: f. Zapata.

Eksempel 2

Du har en lang planke som hylle. For å installere det, tilsvarer det.

I begge tilfeller vil kreftene som balanserer planken ha samme størrelse og retning, og virker på samme handlingslinjer, men blir brukt på forskjellige punkter.

Overførbarhetsprinsippet og øyeblikkene

Anta at det er en styrke F brukt på et punkt A, øyeblikket som stammer fra denne kraften rundt punktet eller vist på figuren er:

MENTEN = rTIL × F

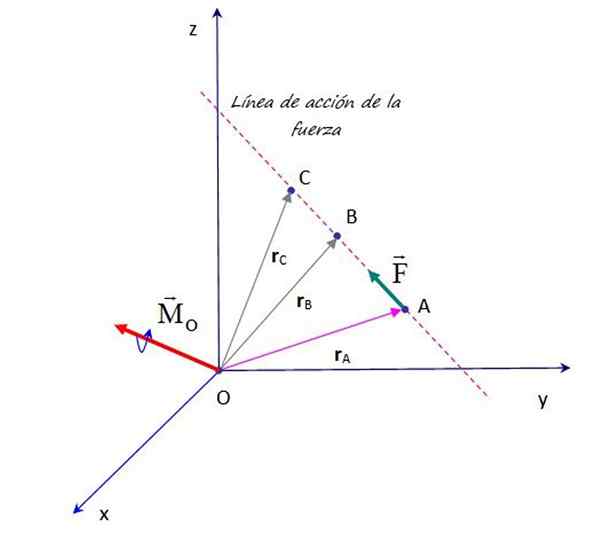Lysbilde eller overføringskraft langs sin handlingslinje endrer ikke øyeblikket den utøver på punktet eller. Kilde: f. Zapata.

Vel, overførbarhetsprinsippet sikrer det F, Å handle på et hvilket som helst punkt langs sin handlingslinje, for eksempel punkt B, C og mer, oppstår det samme øyeblikket med hensyn til punktet eller. Derfor er det gyldig å bekrefte det:

MENTEN = rTIL × F  = rB × F = rC × F

Løste øvelser

Oppgave 1

En homogen sfære har masse m = 5 kg og hviler på en horisontal overflate uten friksjon.

    • a) Tegn inn et opplegg Kraften som utøves av overflaten på sfæren.
    • b) Bygg det frie kroppsskjemaet på sfæren
    • c) Beregn verdien av normalkraften som utøves av overflaten på sfæren.

  • Løsninger A og B

I graf a) Kraften som utøves av overflaten på sfæren vises, kalt normal N, Siden det er vinkelrett på overflaten. Påføringspunktet av styrken sammenfaller med støttepunktet til sfæren på overflaten (punkt i grønt) og handlingslinjen er det vertikale som passerer gjennom det geometriske sentrum av sfæren.

Kan tjene deg: Jordens magnetosfære: Kjennetegn, struktur, gasser

I graf B) er det det frie kroppsdiagrammet til sfæren, der bortsett fra det normale, vises vekten, som brukes i tyngdepunktet, betegnet med det gule punktet.

Takket være overførbarhetsprinsippet, normal kraft N Det kan overføres til dette punktet, uten å endre effekten av det på sfæren. Disse effektene er ikke andre som holder sfæren støttet på bordet i balanse.

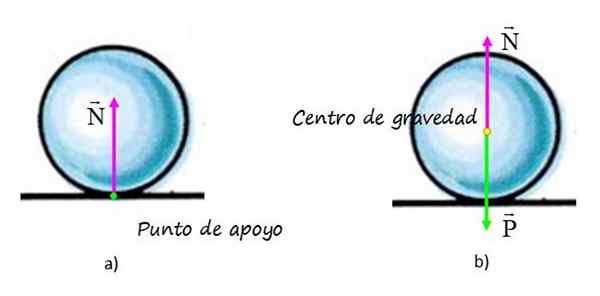I figur a) til venstre virker normalen på sfærenes støttepunkt med overflaten. I figur B), på det frie kroppsdiagrammet overføres normalen til tyngdepunktet, siden vertikalen er dets handlingslinje. Effektene er ikke endret, fordi den balanserer vekten slik at sfæren er i balanse. Kilde: f. Zapata.

  • Løsning c

Siden sfæren er i balanse, tar som en positiv forstand det vertikale opp og negativt det vertikale ned, resulterer Newtons andre lov i:

N - p = 0

Det vil si at vekten og normalen er balansert, derfor er de de samme i størrelsesorden:

N = p = mg = 5 kg × 9.8 m/s2 = 49 n, rettet vertikalt opp.

Oppgave 2

Angi om overførbarhetsprinsippet i følgende tilfeller er oppfylt:

  • Første sak

En kraft på 20 N horisontalt påført et stivt legeme erstattes av en annen kraft på 15 N påført på et annet punkt på kroppen, selv om begge gjelder i samme retning.

    • Løsning

I dette tilfellet vil overførbarhetsprinsippet ikke bli oppfylt, siden de to styrkene gjelder i samme retning, har den andre styrken ikke samme størrelse som den første. Derfor er det ikke gitt en av de uunnværlige forholdene i overførbarhetsprinsippet.

  • Andre sak

En kraft på 20 N horisontalt påført en stiv kropp erstattes av en annen på 20 N, påført på et annet punkt i kroppen og vertikalt.

    • Løsning
Kan tjene deg: Planck Constant: Formler, verdier og øvelser

Ved denne anledningen er overførbarhetsprinsippet ikke oppfylt, selv om de to kreftene har samme modul, gjelder de ikke i samme retning. Igjen er det ikke gitt en av de uunnværlige forholdene i prinsippet om overførbarhet. Det kan sies at de to styrkene er likeverdige.

  • Tredje sak

En kraft på 10 N blir endret horisontalt på en stiv kropp som også brukes på et annet punkt i kroppen, men i samme retning og betydning.

    • Løsning

I dette tilfellet blir overførbarhetsprinsippet oppfylt, siden de to styrkene har samme størrelse og brukes i samme retning og betydning. Alle nødvendige forhold i overførbarhetsprinsippet er oppfylt. Det kan sies at de to styrkene er likeverdige.

  • Fjerde sak

En kraft glir i retning av handlingslinjen din.

    • Løsning

I dette tilfellet blir overførbarhetsprinsippet oppfylt, siden størrelsen på den påførte kraften ikke varierer, og den glir inn i handlingslinjen sin. Igjen blir alle nødvendige forhold i overførbarhetsprinsippet oppfylt.

Øvelse 3

På en stiv kropp gjelder to ytre krefter. De to kreftene gjelder i samme retning og i samme retning. Hvis den første modulen er 15 N og den av den andre av 25 N, hvilke forhold bør en tredje ekstern kraft som erstatter resulteringen av de to foregående for å oppfylle overførbarhetsprinsippet?

  • Løsning

På den ene siden må verdien av den resulterende kraften være 40 N, som er resultatet av å legge til modulen til de to kreftene.

På den annen side må den resulterende styrken handle hvor som helst i den rette linjen som blir med på de to anvendelsespunktene for de to styrkene.

Referanser

  1. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley. 
  2. Øl, f. 2010. Vektormekanikk for ingeniører. McGraw Hill. 5. plass. Utgave.
  3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
  4. Hibbeler, R. 2004. Ingeniørmekanikk: Statistikk. Prentice Hall.
  5. Meriam, J.L. 2012. Ingeniørmekanikk: Statistikk. 7. utgave. Wiley & Sons.