Sekskantet prisme

Vi forklarer hva et sekskantet prisme er, dets egenskaper, elementer, område, hjørner, kanter og hvordan du beregner dem.

Hva er et sekskantet prisme?

EN Sekskantet prisme Det er en tredimensjonal kropp sammensatt av to sekskantform og sider formet som et rektangel eller parallellogram. Det kan finnes i naturen, i den krystallinske strukturen til mineraler som beryllium, grafitt, sink og litium, for eksempel.

Elementene i et sekskantet prisme er basen, ansiktet, kanten, høyden, toppunktet, radio og apothem. Fra dem kan du beregne områder og volum.

Den øvre figuren viser et sekskantet prisme med rektangulære sideflater; det er å si, Et rett sekskantet prisme. Basens sekskanter er vanlige, det vil si at deres indre sider og vinkler er de samme. Imidlertid kan sekskantede prisme ansikter være uregelmessige sekskanter.

Kjennetegn på sekskantet prisme

1- Hexagonal Prism er en tredimensjonal figur med sekskantede baser.

2- Det er et bredt utvalg av objekter som reagerer på denne definisjonen, og likevel er de ganske forskjellige.

I den følgende figuren er det en rekke sekskantede prismer: til venstre et rett sekskantet prisme av vanlige ansikter, til høyre og ned to sekskantede prismer av uregelmessige ansikter. Sekskanten ved basen av prisme nedenfor har en spesiellhet: det er konkav, Noe som betyr at noen av dens indre vinkler er større enn 180 °.

Forskjellige sekskantede prismer. Kilde: Wikimedia Commons.

På den annen side er de sekskantede basene til prismer ovenfor polygoner konveks: Alle indre vinkler måler mindre enn 180 °.

Sekskantede prismeelementer

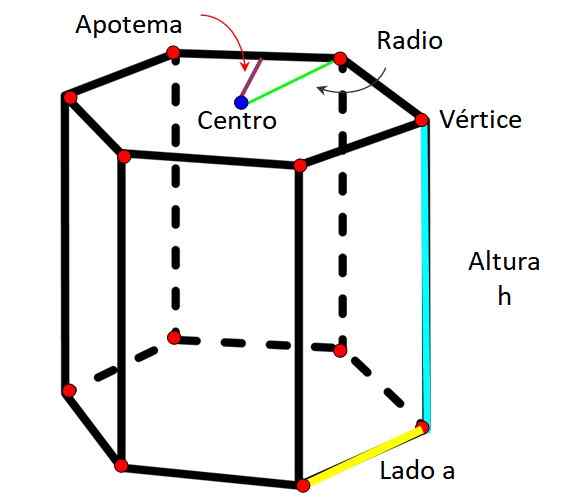Sekskantede prismeelementer. Kilde: f. Zapata

Som hvert prisme er sekskantet prisme preget av å ha følgende elementer:

Kan tjene deg: Multiplikativ omvendt: Forklaring, eksempler, løste øvelser

-Baser: i antall to (2), i form av sekskant og kongruent, det vil si av like stort mål. Sekskantede ansikter kan være regelmessige eller uregelmessige.

-Ansikter: En sekskantet prisme har åtte (8) ansikter totalt, som kan telles ved hjelp av figur 1. Av de 8 ansiktene er to (2) baser og seks (6) er laterale.

-Kant: Det er segmentet som blir med to baser eller to sider av prisme.

-Høyde: Det er avstanden mellom de to ansiktene til prisme. Sammenfaller med lengden på kanten når det gjelder rett prisme.

-Toppunkt: vanlig punkt mellom en base og to sidesider.

Hvis basene til prisme er regelmessig, tillater symmetrien til figuren å definere flere elementer på den vanlige sekskantsiden til.

-Radio: Det er avstanden målt fra midten av sekskanten og ethvert toppunkt.

-Apothem: Det er segmentet som går fra midten av det sekskantede ansiktet til midten av den ene siden.

Ved hjelp av disse elementene beregnes områder og volumer, som vi vil se senere.

Formler

Det er mange formler relatert til sekskantet prisme. De tjener til å beregne området for sidebaser og ansikter, volumet og andre viktige egenskaper. Områdene med vanlig sekskant, uregelmessig sekskant og parallellogram, så vel som omkretsene, er nyttige.

Omkretsen av en flat figur

Det er målet på konturen, som i tilfelle av en polygon som sekskant er summen av sidene. Hvis sekskanten er regelmessig sidelengs til, Det er en formel for omkretsen P:

P = 6.til

Vanlig sekskantområde

La oss ringe ALS og L_TIL På lengden på apotemen. Området er gitt av:

Kan tjene deg: Ikke -grupperte data: Eksempler og trening løst

A = s. L_TIL/2 = 6a. L_TIL/2

Hvor P er omkretsen av figuren.

Avhengig av størrelsen på siden til, Området kan også beregnes av:

A = 2.5981.til²

Uregelmessig sekskantområde

Det er ingen spesifikk formel, siden det avhenger av ordningen på sidene, men sekskanten kan deles inn i trekanter, beregne området til hver og tilsett dem.

En annen metode for å finne området er Gauss Determinants, som det er nødvendig å kjenne koordinatene til sekskanthjørt hjørner.

Parallellogramområde

A = base x høyde

Ja til er basen og h Det er høyden, området er:

A = a.h

Sekskantet prismeområde

Det er summen av områdene i basene -to sekskanter -og ansiktene -6 rektangler eller parallellogrammer-.

Vanlig sekskantet prismeområde

Hvis det sekskantede prisme har basene i form av vanlige sekskanter og sidekantene er vinkelrett på disse basene, er dets område gitt av summen:

A = 2 x 2.5981.til² + 6.h

Hvor til Det er siden av sekskanten og h Det er høyden på prisme.

Uregelmessig og rett sekskantet prismeområde

Hvis basene er uregelmessige sekskanter, beregnes området av:

A = 2a_utgangspunkt  + P.h

Hvor:

-TIL_utgangspunkt Det er det uregelmessige sekskantede baseområdet.

-P er omkretsen av basen.

-H er høyden på prisme

Hjørner

Hvert sekskantet ansikt har 6 hjørner eller hjørner, noe som gir totalt 12 hjørner for det sekskantede prisme.

Kanter

Det er en formel for å finne antall kanter på et prisme. Det ble oppdaget av den store matematikeren Leonhard Euler (1707-1783) og kalles Euler Teorem for Polyhedros. Sier det:

Kan tjene deg: algebraisk resonnement

Hvis C er antall ansikter, og mengden av Vértices V og de totale kantene. Det er sant, det:

C+V = A+2

Beløpene for det sekskantede prisme er: C = 8 og V = 12. Derfor er a:

A = C + V - 2 = 8 + 12-2 = 18

Volum

Volum V av ethvert prisme, enten det er rett eller skrå, av vanlige eller uregelmessige ansikter, er gitt av:

V = baseareal x høyde

Derfor vil vi trenge formlene for området vi så tidligere.

For eksempel, for et rett sekskantet prisme, hvis baser er vanlige sekskanter, er volumet gitt av:

V = 2.5981.til².h

Referanser

1. Matematikk åpen referanse. Polygonområde. Gjenopprettet fra: Mathpenref.com.
2. Wikipedia. Prisme. Gjenopprettet fra: er.Wikipedia.com.