Hva er det magnetiske øyeblikket?

Han Magnetisk øyeblikk Det er en vektor som knytter strømmen som krysser litt eller lukket sløyfe med området av det samme. Modulen er lik produktet av intensiteten til strømmen av området, og dens retning og retning er gitt av høyre regel, som vist i figur 1.

Denne definisjonen er gyldig uansett. Når det gjelder enhet i det magnetiske øyeblikket, i det internasjonale systemet med enheter hvis det er ampere × m².

Figur 1. Den magnetiske momentvektoren til en vilkårlig strømbinding er vinkelrett på planet og retningen bestemmes av høyre tommelregel. Kilde: Wikimedia Commons.

I matematiske termer, betegner Vector Magnetic Moment med de greske tekstene μ (I fet skrift fordi det er en vektor og dermed skiller seg ut fra dens størrelse), uttrykkes den som:

μ = Ia n

Der jeg er intensiteten til strømmen, er a området som omslutter sløyfen og n Det er enhetsvektoren (av modulen lik 1) som peker i retningen vinkelrett på spasens plan, og hvis betydning er gitt av regelen for høyre tommel (se figur 1).

Denne regelen er veldig enkel: krølling av de fire fingrene til høyre hånd slik at de følger strømmen, tommelen indikerer retning og retning av n og derfor det magnetiske øyeblikket.

Den forrige ligningen er gyldig for en loop. Hvis det er nougas som i en spole, multipliseres det magnetiske øyeblikket med n:

μ = nIa n

[TOC]

Magnetisk øyeblikk og magnetfelt

Det er lett å finne uttrykk for det magnetiske øyeblikk av svinger med vanlige geometriske former:

-Kvadratsiden av siden ℓ: μ = Iℓ² n

-Sider rektangulær spiral til og b: μ = Iab n

-Radio R. Radio Spira: μ = Iπr² n

Kan tjene deg: atomnummer

Dipolos magnetfelt

Magnetfeltet produsert av den nåværende sløyfen eller spasen ligner en stangmagnet og også jordens.

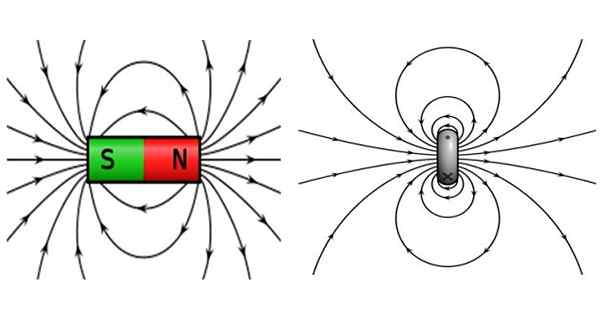Figur 2. Til venstre magnetfeltet til en stangmagnet og til høyre som produserer en sirkulær spiral som transporterer strøm. Kilde: Wikimedia Commons.

Stangmagneter er preget av å ha nordpol og sørpol, der motsatte stolper blir tiltrukket og de samme polene frastøter. Feltlinjene er lukket, forlater nordpolen og når sørpolen.

Nå er de magnetiske stolpene uatskillelige, noe som betyr at hvis en barmagnet er delt inn i to mindre magneter, fortsetter de å ha sine egne nord- og sørpoller. Det er ikke mulig å ha de isolerte magnetiske stolpene, og det er grunnen til at barmagneten kalles Magnetisk dipolo.

Magnetfeltet til en radius r spiral r, som transporterer en strøm i, beregnes av biot-spredningsloven. For punktene som tilhører sin symmetriakse (i dette tilfellet X -aksen), er feltet gitt av:

Hvor μ_enten Det er permeabiliteten til vakuum. Å ta feltet på punkter bort fra spasen, som det er oppfylt at x >> r, nærmer seg feltet:

Forholdet mellom magnetfeltet og det magnetiske momentet til dipolo

Inkludert det magnetiske øyeblikket i forrige uttrykk er:

På denne måten er magnetfeltets intensitet proporsjonal med magnetmomentet. Legg merke til at intensiteten på feltet avtar med avstandskuben.

Denne tilnærmingen gjelder for enhver sløyfe, så lenge som x være stor sammenlignet med dimensjonene.

Og ettersom linjene i dette feltet ligner på stangmagneten, er ligningen en god modell for dette magnetfeltet og den for andre systemer hvis linjer er like, for eksempel: for eksempel:

Kan tjene deg: Absorbans: Hva er, eksempler og øvelser løst

-Partikler lastet i bevegelse som elektron.

-Atomet.

-Jorden og andre planeter og satellitter i solsystemet.

-Stjerner.

Effekt av et eksternt felt på løkken

Et veldig viktig kjennetegn ved det magnetiske øyeblikket er koblingen til dreiemomentet som sløyfen opplever i nærvær av et eksternt magnetfelt.

En elektrisk motor inneholder spoler som en strøm av skiftende retning gjennomgår, og at takket være den ytre feltopplevelsen en sving -effekt. Denne svingen gjør at en akse beveger seg og elektrisk energi blir mekanisk energi under prosessen.

Dreiemoment på en rektangulær sløyfe

Anta at for å lette beregningene, en rektangulær sider til og b, hvis normale vektor n, Utgående skjerm, i utgangspunktet er den vinkelrett på et jevnt magnetfelt B, Som i figur 3. Sidene av sløyfen opplever krefter gitt av:

F = JegL x B

Hvor L Det er en størrelsesvektor lik lengden på segmentet og rettet i henhold til strømmen, og er intensiteten til det samme og B Det er feltet. Kraft er vinkelrett på begge deler L Som feltet, men ikke alle sider opplever styrke.

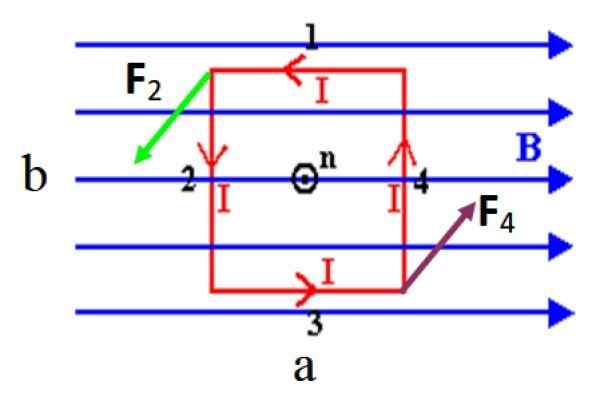Figur 3. En rektangulær spiral som transporterer en strøm I i en anti -Horary Sense, opplever et dreiemoment i nærvær av et ensartet enhetlig magnetfelt. Kilde: f. Zapata.

I figuren som er vist, er det ingen styrke på kortsiden 1 og 3 for å være parallell med feltet, husk at kryssproduktet mellom parallelle vektorer er ugyldig. Imidlertid langsider 2 og 4, som er vinkelrett på B, De opplever betegnede styrker som F₂ og F₄.

Disse kreftene danner et par: De har samme størrelse og retning, men motsatte sanser, derfor er de ikke i stand til å bevege seg til løkken midt på feltet. Men de kan få det til å rotere, siden dreiemomentet  τ At hver kraft utøver, med hensyn til den vertikale aksen som passerer gjennom midten av sløyfen, har den samme retning og betydning.

Kan tjene deg: Samholdsstyrke

I henhold til definisjonen av dreiemoment, hvor r Det er posisjonsvektoren:

τ = r x F

Så:

τ₂ = τ₄=(A/2) F (+J )

Individuelle dreiemomenter blir ikke kansellert, siden de har samme retning og mening, så blir de lagt til:

τ_nett = τ₂ + τ₄ = en f (+J )

Og å være størrelsen på kraften F = IBB, det resulterer:

τ_nett = I⋅a⋅b⋅b (+J )

A⋅B -produktet er område A i spasen, så IAB er størrelsen på det magnetiske øyeblikket μ. Derfor τ_nett = μ⋅B (+J )

Det kan sees at dette generelt sammenfaller med vektorproduktet mellom vektorene μ og B:

τ_nett = μ x B

Og selv om dette uttrykket ble avledet fra en rektangulær sløyfe, er det gyldig for et flatt fotfeste vilkårlig.

Effekten av feltet på løkken er et dreiemoment som har en tendens til å justere det magnetiske øyeblikket med feltet.

Potensiell energi i magnetisk dipol

For å snu spiralen eller dipolen midt på feltet, må det utføres et verk mot magnetkraften, som endrer den potensielle energien til Dipolo. Variasjonen av energi ΔU, når spiralen roterer fra vinkelen θ_enten I vinkelen θ gis av integralen:

Hvis referansenivået er valgt som θ_enten = π/2:

Δu = -μb cos θ

Som igjen kan uttrykkes som skalarproduktet mellom vektorene B og μ:

ΔU = - μ ·B

Den minste potensielle energien i dipolen oppstår når cos θ = 1, noe som betyr det μ og B De er parallelle, energien er maksimalt hvis de er motsatte (θ = π) og er null når de er vinkelrett (θ = π/2).

Referanser

1. Figueroa, d. 2005. Serier: Fysikk for vitenskap og ingeniørfag. Volum 5. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
2. Resnick, r. 1999. Fysisk. Vol. 2. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V.
3. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 2. Pearson.
4. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 2. 7. Ed. Cengage Learning.
5. Tipler, s. (2006) Fysikk for vitenskap og teknologi. 5. utg. Volum 2. Redaksjon tilbake.