Sarrus Rule

Sarrus Rule. Kilde: Bruker: Sevela.P, CC By-SA 4.0, Wikimedia Commons

Hva er Sarrus regel?

De Sarrus Rule Det er en teknikk å beregne determinanter for en firkantet matrise på 3 × 3 eller høyere. Dette systemet lar løsningen være lettere. Det brukes også til å bestemme om vektorsett er lineært uavhengige og danner basen til vektorrommet.

Disse applikasjonene er basert på inverterbarheten til matriser. Hvis en matrise er regelmessig, er determinanten forskjellig fra 0. Hvis det er entall, er determinanten verdt 0. Determinanter kan bare beregnes i firkantede matriser.

For å beregne matriser av hvilken som helst ordre, kan Laplace Teorem brukes. Dette teoremet lar oss forenkle matrisen med høye dimensjoner, i summer av små determinanter som vi bryter ned fra hovedmatrisen.

Sier at determinanten for en matrise er lik summen av produktene fra hver linje eller kolonne, ved determinanten for den tilknyttede matrisen.

Dette reduserer determinantene, slik at en determinant for grad N, blir determinanter for N-1. Hvis vi bruker denne regelen på en påfølgende måte, kan vi få determinanter av dimensjon 2 (2 × 2) eller 3 (3 × 3), der beregningen er mye enklere.

Sarrus Rule

Pierre Frederic Sarrus (1798-1861) var en fransk matematiker. De fleste av dens matematiske traktater er basert på ligningsoppløsningsmetoder og beregning av variasjoner, innenfor numeriske ligninger.

I en av traktatene hans løste han en av de mest komplekse virksomhetene i mekanikken. For å løse problemene med artikulerte stykker, introduserte Sarrus transformasjonen av alternative rettlinjede bevegelser, i ensartede sirkulære bevegelser. Dette nye systemet er kjent som Sarrus -mekanismen.

Det kan tjene deg: eksternalisering og internalisering av kostnadene

Forskningen som ga ham mest var den der han introduserte en ny metode for å beregne determinanter, i artikkelen “Nouvelles Methodes Pour La résolution des équations” (“Ny metode for oppløsning av ligninger”), publisert i 1833. Denne måten å løse lineære ligninger er kjent som Sarrus -regel.

Sarrus -regelen gjør det mulig å beregne determinanten for en 3 × 3 -matrise, uten å bruke Laplaces teorem, og introdusere en mye enklere og mer intuitiv metode. 

For å kunne bekrefte verdien av Sarrus -regelen, tar vi hvilken som helst matrise av dimensjon 3:

Beregningen av dens determinant vil bli utført av produktet fra de viktigste diagonalene, og trekker fra produktet fra de omvendte diagonalene. Dette ville være som følger:

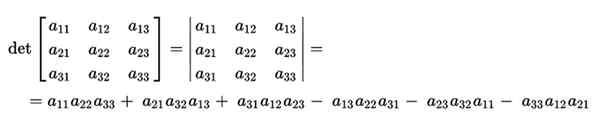
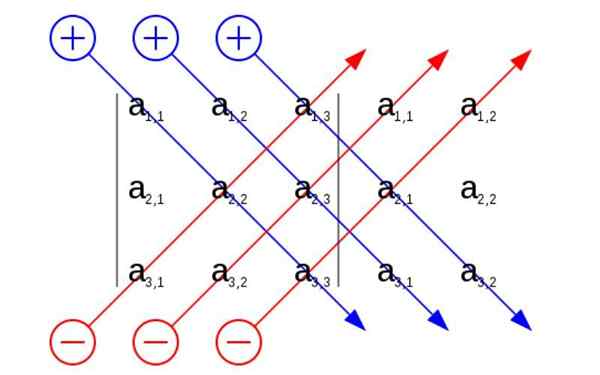
Sarrus -regelen lar oss få en mye enklere visjon når vi beregner diagonalene til determinanten. Det vil bli forenklet ved å legge de to første kolonnene på baksiden av matrisen.

På denne måten er det tydeligere om de viktigste diagonalene og som det omvendte, for beregningen av produktet.

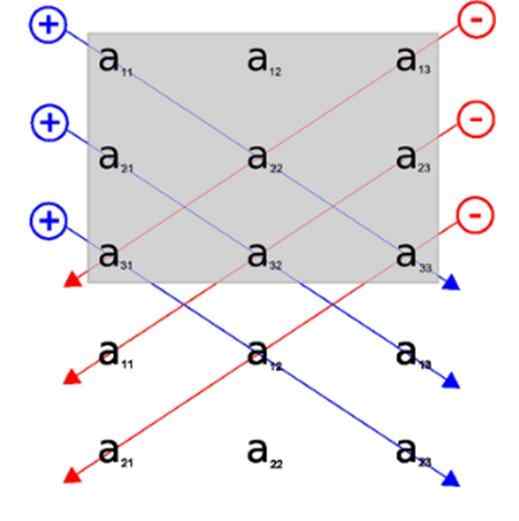
Gjennom dette bildet kan vi se anvendelsen av Sarrus -regelen, inkluderer vi rad 1 og 2, under den grafiske representasjonen av den første matrisen. På denne måten er de viktigste diagonalene de tre diagonalene som vises i utgangspunktet.

De tre omvendte diagonalene er på sin side de som vises først på baksiden.

På denne måten vises diagonalene på en mer visuell måte, uten å komplisere oppløsningen av determinanten, og prøver å finne ut hvilke elementer i matrisen tilhører hver diagonal.

Kan tjene deg: Quechua -ord oversatt til spansk

Som det ser ut i bildet, velger vi diagonalene og beregner produktet som følge av hver funksjon. Diagonalene som vises i blått er de som legger opp. Til summen av disse trekker vi verdien av diagonalene som vises i rødt.

For at komprimering skal være enklere, kan vi bruke et numerisk eksempel, i stedet for å bruke algebraiske termer og subtervilkår.

Hvis vi for eksempel tar noen 3 × 3 -matrise, for eksempel:

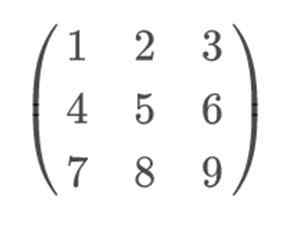
For å bruke Sarrus -regelen og løse den på en mer visuell måte, bør vi inkludere henholdsvis rad 1 og 2, som henholdsvis rad 4 og 5. Det er viktig å opprettholde rad 1 på 4. plassering, og rad 2 i 5. Siden vi utveksler dem, vil ikke Sarrus -regelen være effektive.

For å beregne determinanten, ville matrisen vår være som følger:

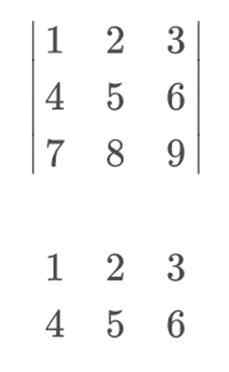
For å fortsette med beregningen, vil vi multiplisere elementene i hoveddiagonalene. Den synkende at de begynner til venstre vil bære et positivt tegn, mens de omvendte diagonalene, som er de som begynner til høyre, har et negativt tegn.

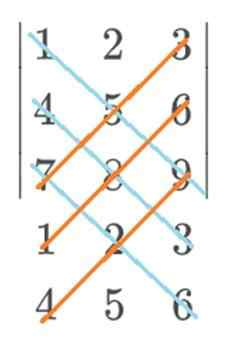
I dette eksemplet ville det blå gå med et positivt tegn og det røde med et negativt tegn. Den endelige beregningen av Sarrus -regelen vil forbli på denne måten:

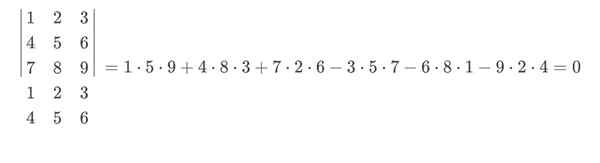
Folkens av determinanter

Determinant for dimensjon 1

Hvis matrisedimensjonen er 1, er matrisen på denne måten: a = (a)

Derfor vil dets determinant være som følger: det (a) = | a | = a

Oppsummert er determinanten av matrise A lik den absolutte verdien av matrise A, som i dette tilfellet er en.

Dimensjon determinant 2

Hvis vi går til matriser i dimensjon 2, får vi matriser av typen:

Kan tjene deg: taumatikk

Der determinanten er definert som:

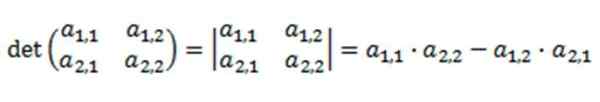
Oppløsningen av denne determinanten er basert på multiplikasjonen av dens viktigste diagonale, og trekker produktet av den omvendte diagonalen.

Determinant for dimensjon 3

Hvis matrisedimensjonen er 3, vil den resulterende matrisen være av denne typen:

Determinanten for denne matrisen vil bli løst gjennom Sarrus -regelen på denne måten:

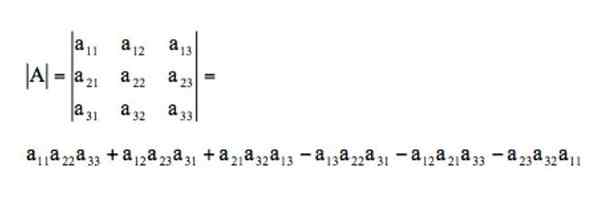
Referanser

1. Anthony Nicolaides (1994). Determinanter og matriser. Passpublikasjon.
2. M. Casteleiro Villalba (2004). Introduksjon til lineær algebra. ESIC -redaksjon.