Matte

Rektangulært koordinatsystem

Rektangulært koordinatsystem
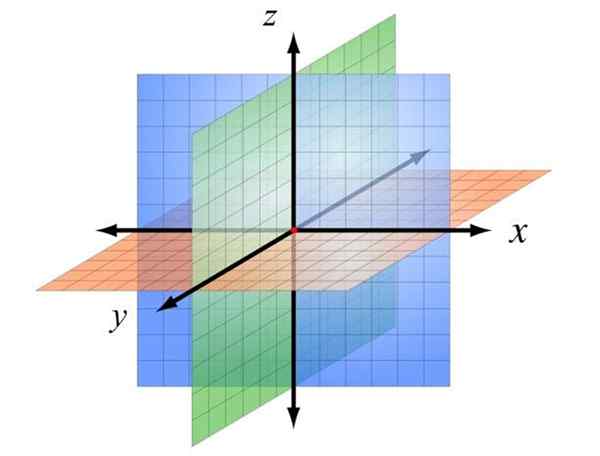
Kartesisk koordinatsystem i tre dimensjoner. Kilde: Wikimedia Commons

Hva er det rektangulære koordinatsystemet?

I matematikk og geometri, a Rektangulært koordinatsystem Det tjener til nøyaktig å finne ethvert punkt på verdensrommet. For dette er det nok å gi tre koordinater.

Konstruksjonen av systemet i planet er veldig enkelt, bare tre linjer som vil være koordinataksene eller kartesiske akser er nødvendig: en vertikal, en annen horisontal og en tredjedel som kommer inn eller forlater papiret eller skjermen.

Disse aksene er gjensidig vinkelrett og skjæringspunktet er opprinnelse av systemet.

Denne bestemmelsen er vist på figuren over, der brevene er tildelt bokstavene x, og, z, å skille dem. På denne måten bestemmes tre plan, med opprinnelsen farget i rødt.

Flyet Xz, I blått er det planet på skjermen og er foran leserens øyne. Flyet Xy Den er oransje, og kan være assosiert med bordet eller gulvet. Endelig flyet zy I grønt er det vinkelrett på de forrige og del skjermen eller papiret i to regioner.

Kvadrikulering av hver av disse flyene og tildeler en skala, kan du plassere et hvilket som helst punkt i rommet og gir de respektive koordinatene X og z, Alltid i den rekkefølgen, for å unngå uklarheter.

For hvaDet serverer det rektangulære koordinatsystemet?

Det rektangulære koordinatsystemet tjener til å plassere ethvert punkt i rommet eller i flyet, nok til å indikere de tre koordinatene til punktet, i rekkefølge x, y, z.

Det kan tjene deg: nominell variabel: konsept og eksempler

Hvis punktet tilhører et plan, vil et av koordinatene være 0, og hvis det er på noen av aksene, vil to av koordinatene være 0, bortsett fra at tilsvarer stedet for punktet, bortsett fra opprinnelsen, som, som som som som som sa før, har koordinater (0.0.0).

Følgende eksempler avklarer ovennevnte.

Eksempler

Eksempel 1

Et hvilket som helst punkt P på x -aksen uttrykkes gjennom koordinater P (x, 0, 0). Merk at opprinnelsen, fremhevet i rødt i følgende figur, har koordinater eller (0, 0, 0).

Når poenget er til høyre for opprinnelsen, har den positiv x -koordinat, mens hvis det er til venstre, er det negativt. For eksempel har P1 Blue Point koordinater (6,0,0), mens punkt P2 i grønt, har koordinater (-9,0,0).

Eksempel 2

I den følgende figuren er det to akser, som er X akse den horisontale aksen og Axis y Det vertikale. Med dette er det nok å representere punkter i flyet, to koordinater er nødvendige. Opprinnelsen eller er poenget (0,0).

Legg merke til at disposisjonen til aksene deler flyet inn i fire regioner som kalles Kvadranter. Aksene over og til høyre for opprinnelsen er utpekt med et positivt tegn, mens de nedenfor og til venstre skilles ut med et negativt tegn.

Deretter tilsvarer poengene hvis koordinater er positive begge deler, den første kvadranten eller kvadranten i. Green Point har koordinater (2,3) og er i I -kvadranten.

For sin del har det røde punktet koordinater (-3,1) og er i II-kvadranten, mens koordinatene til det blå punktet er (-1.5; -2.5) Og det er i III -kvadranten.

Kan tjene deg: Vanlig faktorisering: eksempler og øvelser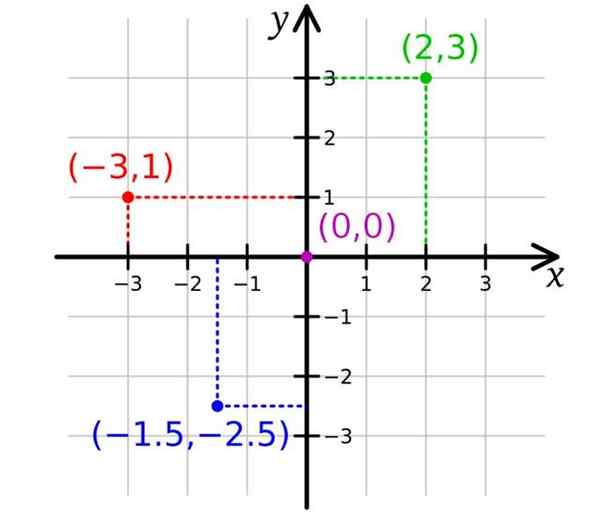 Kartesisk plan. Kilde: Wikimedia Commons

Eksempel 3

Følgende er et eksempel på et punkt i verdensrommet. Koordinatene er x = 6, y = 10 og z = 8, derfor p (6,10,8).

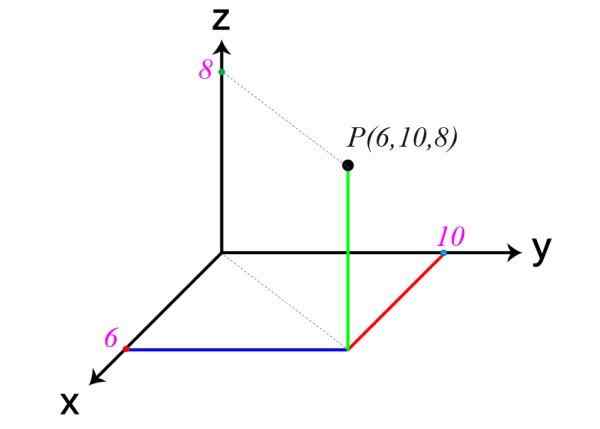Et annet eksempel på kartesiske akser

I begynnelsen av begynnelsen blir det advart om at planene XY, XZ og Zy deler plassen i åtte regioner, kalt Octavers. Punkt P i eksemplet er i første ocant.

Referanser

  1. Alexander, d. (2013). Geometri. 5. plass. Utgave. Cengage Learning.
  2. Larson, r. (2012). Forkalkning. 8. Utgave. Cengage Learning.
  3. Stewart, J. (2007). Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
  4. Det kartesiske flyet. Hentet fra: DL.UNCW.Edu.
  5. Weisstein, e. Kartesiske koordinater. Gjenopprettet fra: Mathworld.Wolfram.com