Bue (geometri) mål, typer buer, eksempler

Han Bue, I geometri er det en hvilken som helst buet linje som forbinder to punkter. En buet linje, i motsetning til en rett linje, er at hvis retning er annerledes på hvert punkt av det samme. Det motsatte av en bue er et segment, siden dette er en rett seksjon som blir med to poeng.

Buen som ofte brukes i geometri er omkretsbuen. Andre buer med vanlig bruk er den parabolske buen, elliptiske buen og den kriminelle buen. Bueformen brukes også ofte i arkitektur som et dekorativt element og strukturelt element. Dette er tilfellet med overligningene til dørene og vinduene, så vel som av broer og akvedukter.

Figur 1. Regnbuen er en buet linje som blir med to punkter i horisonten. Kilde: Pixabay

[TOC]

Buen og dens mål

Målet på en lysbue er dens lengde, som avhenger av typen kurve som forbinder de to punktene og plasseringen av dem.

Lengden på en sirkulær lysbue er en av de enkleste å beregne, fordi den fulle lysbueens lengde eller omkrets av en sirkel er kjent.

Omkretsen av en sirkel er to pi ganger radioen din: P = 2 π r. Å vite dette, hvis du vil beregne lengden s av en sirkulær bue med vinkel α (målt i radianer) og radio R, En andel brukes:

(s / p) = (α / 2 π)

Deretter rydding s av det forrige uttrykket og erstatte omkretsen p av uttrykket avhengig av radioen R, Du har:

S = (α / 2 π) p = (α / 2 π) (2 π r) = α r.

Det vil si at målet på en sirkulær lysbue er et produkt av dens vinkelåpning av den sirkulære lysbueradius.

For en bue på en generell måte er problemet mer komplisert, til det punktet at de store tenkere av antikken hevdet at det var en umulig oppgave.

Det kan tjene deg: Hva er algebraiske uttrykk og som er de hyppigste?

Det var ikke før ankomst av differensialen og integrert beregning i 1665, at måleproblemet ble løst tilfredsstillende. 

Før oppfinnelsen av differensialberegningen, kunne bare løsninger bli funnet ved bruk av polygonal linje eller omkretsbuer som nærmet seg den sanne buen, men disse løsningene var ikke nøyaktige. 

Typer buer

Fra geometriens synspunkt er buene klassifisert i henhold til den buede linjen som blir med to punkter i flyet. Det er andre klassifiseringer i henhold til dens arkitektoniske bruk og form.

Sirkulær bue

Når linjen som forbinder to punkter i flyet er et stykke omkrets av en viss radius, er det en sirkulær bue. Figur 2 viser en sirkulær bue med radius R som kobler punkt A og B.

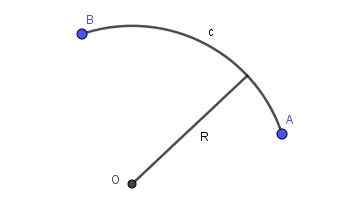Figur 2. Radio R sirkulær lysbue som kobler punkt A og B. Utarbeidet av Ricardo Pérez.

Parabolsk bue

Lignelsen er banen som følger et objekt som har blitt kastet i luften i skrå form. Når kurven som blir med to punkter er en lignelse, er det en parabolsk bue som den som er vist i figur 3.

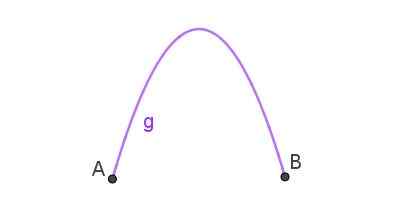Figur 3. Parabolsk bue som kobler punktene A og B. Utarbeidet av Ricardo Pérez.

Dette er formen som vedtar vannstrålen som kommer ut av en slange som peker opp. Den parabolske buen kan observeres i vannkildene.

Figur 4. Parabolsk bue dannet av vann fra en kilde i Dresden. Kilde: Pixabay.

Katurerbue

Kontrollbuen er en annen naturlig bue. Kontrollen er kurven som naturlig dannes når en kjede eller et tau henger komfortabelt fra to separate punkter.

Kan tjene deg: Hva er elementene i en vinkel?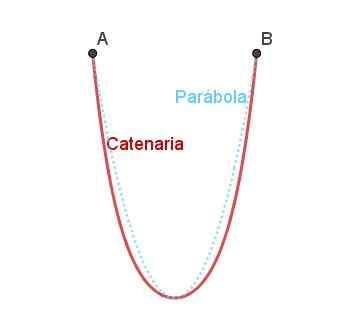 Figur 5. Kontrollbue og sammenligning med den parabolske buen. Utarbeidet av Ricardo Pérez.

Kontrollen ligner på parabolen, men den er ikke akkurat den samme som det kan bemerkes i figur 4.

Den omvendte kriminalsøkten brukes i arkitektur som et strukturelt element av høy kompresjonsmotstand. Faktisk kan det påvises at det er den mest resistente buetypen blant alle mulige former. 

For å bygge en solid ledningsbue, blir bare formen på et tau eller kjede kopiert, deretter blir den kopierte formen for å reprodusere den i døren eller vinduet.

Elliptisk bue

En bue er elliptisk hvis kurven som kobler to punkter er en strekning eller strekning av ellipse. Ellipsen er definert som det geometriske stedet for punktene hvis avstand til to punkter som gis alltid tilfører et konstant beløp.

Ellipsen er en kurve som vises i naturen: det er kurven for planetens bane rundt solen, som Johannes Kepler demonstrerte i 1609.

I praksis kan en ellipse trekkes ved å sette to stag på gulvet eller to pinner på papir og bundet et tau til dem. Da er tauet anspent med markøren eller blyanten og kurven trekkes. Et stykke ellipse er en elliptisk bue. Følgende animasjon illustrerer hvordan ellipsen tegnes:

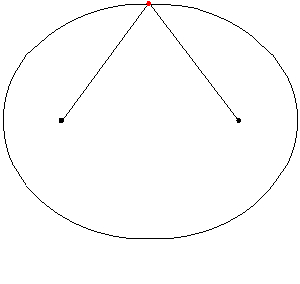Figur 5. Posen av en ellipse ved hjelp av et spent tau. Kilde: Wikimedia Commons

Figur 6 viser en elliptisk lysbue som kobler punktene G og H.

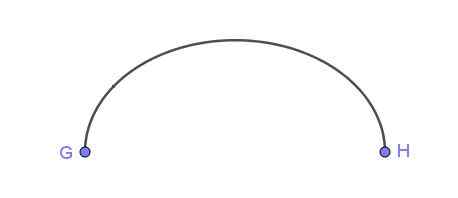Figur 6. Elliptisk lysbue som kobler sammen to punkter. Utarbeidet av Ricardo Pérez.

Eksempler på buer

Følgende eksempler refererer til hvordan du beregner omkretsen til noen spesifikke buer.

Kan tjene deg: transcendente tall: hva er, formler, eksempler, øvelser

Eksempel 1

Figur 7 viser at et vindu ble endt i kuttet sirkulærbue. Dimensjonene vist på figuren er på føttene. Beregn buelengden.

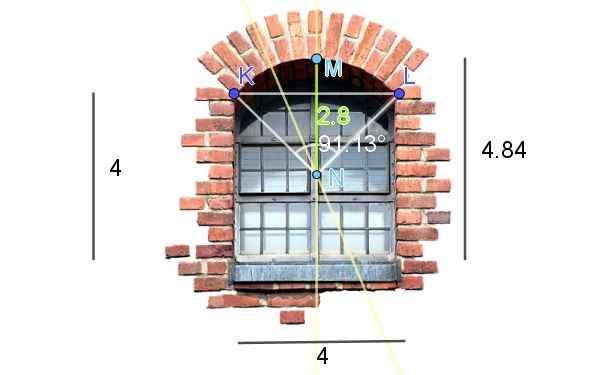Figur 7. Beregning av den sirkulære buelengden på et vindu. (Egne merknader - vindusbilde i pixabay)

For å få sentrum og radius for den sirkulære buen til vinduets overliggende konstruksjoner er laget på bildet:

-KL -segmentet er tegnet og dets mediatrix er trukket.

-Da ligger det høyeste punktet i overliggeren, som vi kaller m. KM -segmentet blir deretter vurdert og mediatrixen trekkes.

Avskjæringen av de to mediatriser er punkt N og er også sentrum av den sirkulære buen.

-Nå må du måle lengden på NM -segmentet, som sammenfaller med radius r på sirkulærbuen: r = 2.8 fot.

-For å vite lengden på buen i tillegg til radius, vinkelen som danner buen. Som kan bestemmes ved to metoder, eller måles med en transportør, eller vekselvis beregnet ved bruk av trigonometri.

I tilfelle vist vinkelen som danner buen er 91,13º, som må konverteres til radianer:

 91,13º = 91,13º * π / 180º = 1,59 radianer

Vi beregner endelig lengden s av buen gjennom formelen S = α r.

S = 1,59 * 2.8 fot = 4,45 fot

Eksempel 2

Finn lengden på den elliptiske buen vist i figur 8, kjent r og den mindre semi -aksen s av ellipsen.

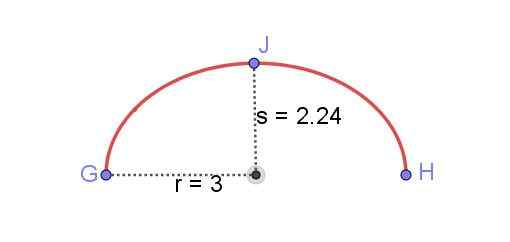Figur 8. Elliptisk bue mellom GH. Utarbeidet av Ricardo Pérez.

Å finne lengden på en ellipse var i lang tid et av de vanskeligste problemene med matematikk. Løsninger uttrykt ved elliptiske integraler kan oppnås, men for å ha en numerisk verdi, må disse integralene i kraftserien utvides. Et eksakt resultat vil kreve uendelige vilkår i disse seriene.

Heldigvis fant det matematiske geniet av hinduistisk opprinnelse Ramanujan, som bodde mellom 1887 og 1920, en formel som tilnærmer seg veldig presist omkretsen til en ellipse:

Omkrets av en ellipse = π [3 (r + s) - √ ((3r + s) (r + 3s))]]

Omkretsen til en ellipse med R = 3 cm og S = 2.24 cm er 16,55 cm. Imidlertid har den elliptiske buen som er vist halvparten av den verdien:

Elliptisk lysbue lengde GH = 8.28 cm.

Referanser

1. Clemens s. 2008. Geometri og trigonometri. Pearson Education.
2. Garcia f. Numeriske prosedyrer i Java. Lengde på en ellipse. Hentet fra: SC.Ehu.er
3. Dynamisk geometri. Buer. Gjenopprettet fra Geometriadinamica.er
4. Pizedas. Ellipser og lignelser rundt oss. Hentet fra: Pizedas.com
5. Wikipedia. Arc (geometri). Gjenopprettet fra: det er.Wikipedia.com