Gratis konseptkonsept, ligninger, øvelser løst

De fritt fall Det er den vertikale bevegelsen som en gjenstand opplever når den slippes fra en viss høyde nær jordoverflaten. Det er en av de enkleste og mest umiddelbare bevegelsene som er kjent: i en rett linje og med konstant akselerasjon.

Alle objekter som slippes, eller som blir kastet vertikalt opp eller ned, beveger seg med akselerasjonen på 9.8 m/s² levert av jordens alvorlighetsgrad, uavhengig av dens masse.

Fritt fall fra en klippe. Kilde: Pexels.com.

Dette faktum kan aksepteres i dag uten problemer. Å forstå den sanne naturen til fritt fall tok imidlertid en stund. Grekerne hadde allerede beskrevet det og tolket veldig i utgangspunktet mot det fjerde århundre A C.

[TOC]

Ligninger av fritt fallbevegelse

Når den er overbevist om at akselerasjon er den samme for alle kroppene som frigjøres under virkningen av tyngdekraften, er det på tide å etablere de nødvendige ligningene for å forklare denne bevegelsen.

Det er viktig å understreke at luftmotstand ikke tas med i denne første bevegelsesmodellen. Resultatene fra denne modellen er imidlertid veldig presise og nær virkeligheten.

I alt som følger vil partikkelmodellen antas, det vil si at dimensjonene til objektet ikke blir tatt i betraktning, forutsatt at hele massen er konsentrert på et enkelt punkt.

For en jevn akselerert rettlinjet bevegelse blir den tatt som en referanseakse til aksen og. Den positive sansen blir tatt opp og den negative ned.

De kinematiske størrelsene

På denne måten er ligningene av posisjonen, hastigheten og akselerasjonen avhengig av tiden:

Akselerasjon

A = g = -9.8 m/s² (-32 fot/s²)

Posisjon avhengig av tid: og T)

y = y_enten + v_enten . T + ½ GT²

Hvor og_enten Det er startposisjonen til mobilen og v_enten er den første hastigheten. Husk at i den vertikale lanseringen er den innledende hastigheten nødvendigvis forskjellig fra 0.

Som kan skrives som:

og - og_enten = v_enten . T + ½ GT²

Δy = v_enten . T + ½ GT²

Med Δog Å være forskyvningen laget av den mobile partikkelen. I enheter av det internasjonale systemet er både posisjonen og forskyvningen gitt i meter (m).

Hastighet avhengig av tid: V (t)

v = v_enten + g . t

Hastighet avhengig av forskyvning

Det er mulig å utlede en ligning som kobler forskyvning med hastighet, uten å gripe inn tid. For å gjøre dette blir tiden for den siste ligningen fjernet:

Kan tjene deg: kvantemekanisk modell av atomet

 Og den erstattes i forskyvningsligningen:

Δy = v_enten . T + ½ GT²

Torget er utviklet ved hjelp av det bemerkelsesverdige produktet og begrepene er omgruppert.

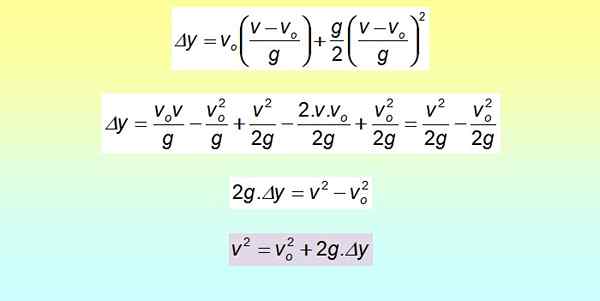
Denne ligningen er nyttig når tiden ikke er tilgjengelig, men i stedet er det hastigheter og forskyvninger, som det vil bli sett i delen av løste eksempler.

Eksempler på fritt fall

Den imøtekommende leseren vil ha lagt merke til tilstedeværelsen av den første hastigheten V_enten. De tidligere ligningene er gyldige for vertikale bevegelser under virkning av tyngdekraften, både når objektet faller fra en viss høyde, som om det kastes vertikalt opp eller ned.

Når objektet synker, er det ganske enkelt gjort v_enten = 0 og ligninger er forenklet som følger.

Akselerasjon

A = g = -9.8 m/s² (-32 fot/s²)

Posisjon avhengig av tid: og T)

y = y_enten+ ½ gt²

Hastighet avhengig av tid: V (t)

v = g . t

Hastighet avhengig av forskyvning

v² = 2g. Dy

Dy Det vil også være negativt, siden v² Det må være en positiv mengde. Dette vil skje både hvis opprinnelse enten null av koordinatsystemet ved lanseringspunktet eller på bakken.

Hvis leseren foretrekker det, kan det ta retningen nedover som positiv. Tyngdekraften vil fortsette å handle hvis det antas at det er + 9.8 m/s². Men du må være i samsvar med de valgte tegnkonvensjonen.

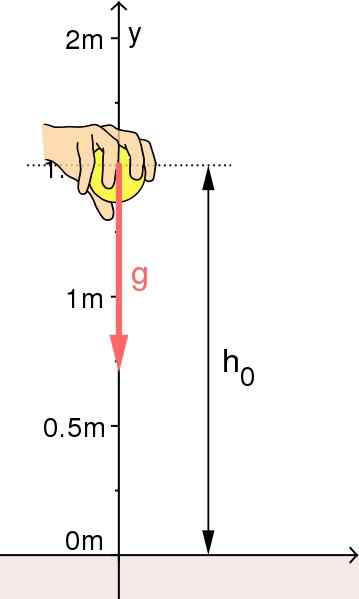Et objekts fritt fall: Opprinnelsen til referansesystemet er valgt på bakken. Kilde: Kilde: Mikerun [CC BY-SA 4.0 (https: // creativecommons.Org/lisenser/by-SA/4.0)]

Vertikal lansering opp

Her kan naturlig nok ikke starthastigheten være null. Vi må gi objektet for en impuls å gå opp. I henhold til den innledende hastigheten som er gitt, vil objektet stige til større eller mindre høyde.

Selvfølgelig vil det være et øyeblikk hvor objektet øyeblikk stopper opp. Da vil den maksimale høyden blitt nådd med hensyn til lanseringspunktet. Også akselerasjonen er fortsatt ned. La oss se hva som skjer i dette tilfellet.

Beregning av den maksimale høyden nådd

Velge meg = 0:

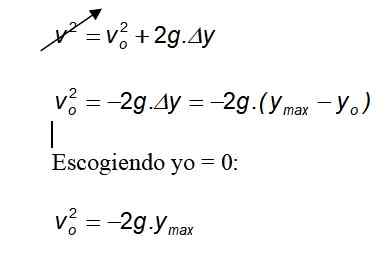
Ettersom tyngdekraften alltid peker på bakken i negativ retning, blir det negative tegnet kansellert.

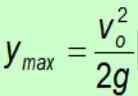
Maksimal tidsberegning

En lignende prosedyre tjener til å finne tiden det tar for objektet å nå maksimal høyde.

v = v_enten + g . t

Det gjør det v = 0

v_enten = - g . t_Maks

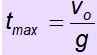
Flytid er tiden som gjenstanden varer i luften. Hvis objektet går tilbake til utgangspunktet, er stigningstiden lik nedstigningstiden. Derfor er flytid 2. T maks.

Kan tjene deg: Mikroskopisk skala: egenskaper, tellepartikler, eksempler

Er det dobbelte av T_Maks Den totale tiden som gjenstanden varer i luften? Ja, så lenge objektet starter fra et punkt og går tilbake til det.

Hvis lanseringen er laget av en viss høyde på bakken og objektet får lov til å fortsette til dette, vil flytiden ikke lenger være det dobbelte av maksimal tid.

Løste øvelser

I oppløsningen av øvelsene som følger, vil følgende bli vurdert:

1-Høyden der objektet slippes er liten sammenlignet med jordens radius.

2-Luftmotstanden er foraktelig.

3-Verdien av akselerasjonen av tyngdekraften er 9.8 m/s²

4-Når det er problemer med en enkelt mobil, er det helst valgt og_enten = 0 på utgangspunktet. Dette letter vanligvis beregninger.

5-på mindre enn det motsatte er indikert, blir den oppadgående retningen tatt som positiv.

6 -I de stigende og synkende kombinerte bevegelsene gir ligningene som brukes direkte de riktige resultatene, så lenge konsistensen opprettholdes med tegnene: opp positivt, ned negativ og alvorlighetsgrad -9.8 m/s² eller -10 m/s² Hvis du foretrekker å runde (for mer komfort når du beregner).

Oppgave 1

En ball kastes vertikalt opp med en hastighet på 25.0 m/s. Svar på følgende spørsmål:

a) Hvor mye stiger det?

b) Hvor lang tid tar det å oppnå sitt høyeste punkt?

c) Hvor lang tid tar ballen å berøre jordoverflaten etter at den oppnår sitt høyeste punkt?

d) Hva er hastigheten din når du kommer tilbake til nivået av hvor den startet?

Løsning

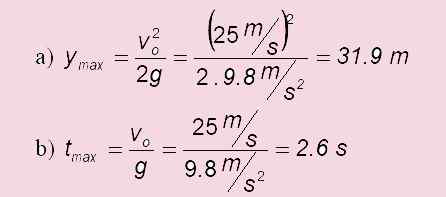
c) I tilfelle av en nivå lansering: t_flygning = 2 . t_Maks = 2 x6 s = 5.1 s

d) Når den går tilbake til utgangspunktet, har hastigheten samme størrelse som starthastigheten, men motsatt retning, derfor må den være - 25 m/s. Det kontrolleres enkelt ved å erstatte verdier i ligningen for hastighet:

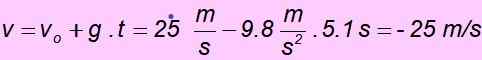
Oppgave 2

En liten postsaker frigjøres fra et helikopter som er synkende med konstant hastighet på 1.50 m/s. Etter 2.00 S Beregn:

a) Hva er hastigheten på kofferten?

b) Hvor langt er kofferten under helikopteret?

c) Hva er svarene dine for seksjoner a) og b) hvis helikopteret stiger med konstant hastighet på 1.50 m/s?

Løsning

Avsnitt a

Når du forlater helikopteret, bærer kofferten den første hastigheten på det, derfor v_enten = -1.50 m/s. Med den angitte tiden har hastigheten økt takket være akselerasjonen av tyngdekraften:

Kan tjene deg: himmellegemer

v = v_enten + g . t = -1.50 - (9.8 x 2) m/s = - 21.1 m/s

Avsnitt b

La oss se hvor mye kofferten har gått ned med hensyn til utgangspunktet på den tiden:

Koffert: Dy = v_enten . T + ½ GT² = -1.50 x 2 + ½ (-9.8) x 2² M = -22.6 m

Den er valgt og_enten = 0 På utgangspunktet, som antydet i begynnelsen av seksjonen. Det negative tegnet indikerer at kofferten har kommet ned 22. 6 m under utgangspunktet.

I mellomtiden helikopteret Det har falt Raskt -1.50 m/s antar vi hele tiden, derfor i den indikerte tiden på 2 sekunder har helikopteret reist:

Helikopter: Δy = v_enten.t = -1.femti x 2 m = -3 m.

Derfor etter 2 sekunder skilles kofferten og helikopteret med en avstand fra:

D =| -22.6 - (-3) | M = 19. 6 m.

Avstanden er alltid positiv. For å fremheve dette brukes den absolutte verdien.

Avsnitt C

Når helikopteret stiger, har det en hastighet på + 1.5 m/s. Med den hastigheten kommer kofferten ut, slik at etter at 2 sek allerede bærer:

v = v_enten + g . T = +1.50 - (9.8 x 2) m/s = - 18.1 m/s

Hastigheten viser seg å være negativ, siden kofferten etter 2 sekunder beveger seg. Har økt takket være tyngdekraften, men ikke så mye som i avsnitt A.

Nå vil vi finne hvor mye kofferten har kommet ned med hensyn til utgangspunktet i løpet av de første to sekundene av reisen:

Valija: Δy = v_enten . T + ½ GT² = +1.50 x 2 + ½ (-9.8) x 2² M = -16 .6 m

I mellomtiden helikopteret Det har steget Angående utgangspunkt, og har gjort det med konstant hastighet:

Helikopter: Δy = v_enten.T = +1.femti x 2 m = +3 m.

Etter 2 sekunder er kofferten og helikopteret atskilt med en avstand fra:

D =| -16.6 - (+3) | M = 19.6 m

Avstanden som skiller dem er den samme i begge tilfeller. Kofferten reiser mindre vertikal avstand i det andre tilfellet, fordi dens første hastighet ble rettet oppover.

https: // youtu.BE/W2UVETXWSFK

Referanser

1. Kirkpatrick, l. 2007. Fysikk: En titt på verden. 6^ta Forkortet utgave. Cengage Learning.  23 - 27.
2. Rex, a. 2011. Fundamentals of Physics. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14^th. Ed. Volum1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9^na Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Fysikk 10. Pearson Education. 133 - 149.