Mackinder Box

Hva er Mackinder -boksen?

De Mackinder Box Det er et metodologisk element med flere applikasjoner i matematikk. Hjelp med å undervise i grunnleggende operasjoner: sum, subtraksjon, multiplikasjon og inndeling. Det brukes også til å skille undergruppe av sett og lage kardinal subtraksjon; Det tjener til å bryte ned og komponere additive tallstrukturer.

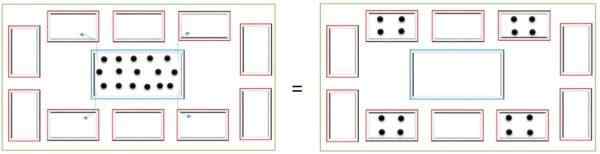
I utgangspunktet handler det om å plassere en stor sentral beholder og 10 mindre containere rundt. Innenfor de mindre beholderne er enhetsmengder representert, som deretter vil bli avsatt i en større beholder, for å representere at et beløp legges til, og refererer til den progressive summen eller multiplikasjonen.

Motsatt kan du også representere at et beløp blir trukket tilbake fra hovedboksen, og refererer til divisjonen.

Hva er Mackinder -boksen for?

Mackinder Box er en metode som ble utviklet i 1918 i Chelsea, England, av Jessie Mackinder, som var lærer for den byen.

Denne metoden tar sikte på å fremme individualisering av utdanning i fag som matematikk, lesing og skriving, ved hjelp av enkle, men interessante materialer som containere, kort og vesker, som brukes fritt.

Dette instrumentet består av ti containere som er rundt en større sentral beholder, alle plassert på en flat base. Disse elementene tjener til å utføre grunnleggende matematiske operasjoner, for eksempel å legge til, trekke, multiplisere og dele. Den kan også brukes til å skille sett og undergruppe.

Mackinders boks brukes i de første årene av utdanning. Det letter forståelsen av matematikk fordi metodikken deres er basert på bruk av undervisningsmateriell, og gir friheten som hver deltaker manipulerer eller samhandler direkte med materialet.

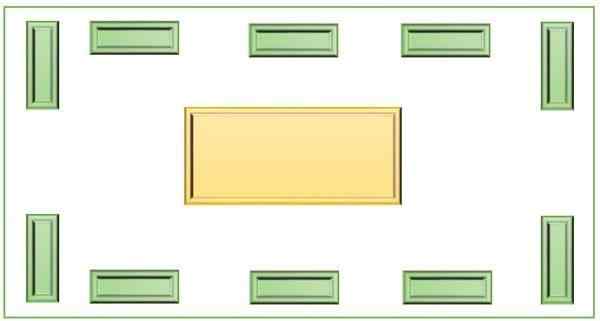
Hvordan gjøre det?

Mackinder -boksen består av veldig grunnleggende elementer. For å danne det, kan til og med resirkuleringsmateriale eller hvilken som helst type beholder som serverer små gjenstander som representerer enhetene som vil telles, brukes til og med. Blant de vanligste måtene å gjøre det på er følgende:

Med pappesker

Følgende materiale vil være nødvendig:

• En rektangulær base, som kan være laget av papp (skoboks) eller papp.
• 10 små pappesker. De kan være bokser med fyrstikker.
• 1 større boks.
• Lim.
• Ark, fosforpinner, frø eller papirkuler, som kan brukes til å telle.

Med plastbeholdere

Materialene som skal brukes er følgende:

• En rektangulær base, laget av papp (skoboks) eller papp.
• 10 plastbeholdere, som er små.
• En stor plastbeholder; For eksempel en CD -boks.
• Lim.
• Chips, fosforpinner, frø eller papirkuler, som kan brukes til å telle.

Fremgangsmåte

• Skjær den rektangulære basen.
• I midten er den større beholderen (pappboksen eller plastbeholderen) festet).
• Rundt den store beholderen er de minste beholderne limt og slippes ut.
• Beholderne i forskjellige farger kan males, og den har lov til å tørke.
• Brikkene, fyrstikkene med fyrstikker, frø, papirkuler eller ethvert element som brukes til å telle, kan forbli lagret i en annen beholder eller inne i den sentrale beholderen.

Bruk eksempler

Med Mackinder -boksen kan grunnleggende matematikkoperasjoner utføres, under hensyntagen til at containerne representerer gruppene eller settene, mens elementene i hver av disse vil være chips, frø, papirkuler, blant andre.

Sum eller tillegg

For å lage en sum brukes to små bokser. I en av disse brikkene som representerer den første tilsetningen er plassert, og i den andre boksen er arkene til den andre tilsettingen plassert.

Du begynner å telle kortene på boksen som har minst mulig mengde av disse og er plassert i den sentrale boksen; På slutten med brikkene til den første boksen fortsetter den andre.

For eksempel, hvis du i den ene boksen har 5 chips og i den andre 7, begynner du å telle fra den som har 5 chips, og plasserer dem i sentralboksen til du når 5. Fortsett deretter med brikkene til den andre boksen og så videre til den når 12.

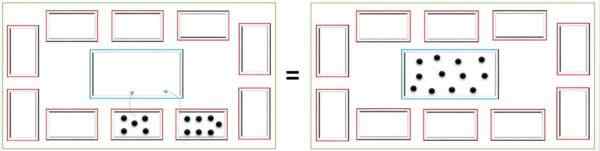
Subtraksjon eller subtraksjon

Å trekke fra alle brikkene som representerer minuenden; det vil si til det totale beløpet som et annet beløp vil bli trukket fra (stjålet).

Fra den store boksen er mengden chips du vil trekke fra, fjernet, de teller og plasserer i en av de små boksene. For å kjenne til subtraksjonsresultatet er det antall brikker som gjensto inne i den store boksen.

For eksempel er det 10 chips i sentralboksen og 6 brikker skal trekkes fra. Disse fjernes og plasseres i en av de små boksene; Deretter, teller brikkene som ble igjen i den store boksen, er det totalt 4 brikker som representerer resultatet av subtraksjonen.

Multiplikasjon

Multiplikasjon består i å legge til samme tall flere ganger. Med Mackinder Box representerer det første multiplikasjonsproblemet gruppene som vil bli dannet; det vil si antall små bokser som vil bli okkupert.

På den annen side indikerer det andre tallet antall elementer som hver gruppe vil ha, eller brikkene som vil bli plassert i hver liten boks. Deretter blir alle brikkene til hver liten boks fortalt og plassert i den sentrale boksen, for å oppnå resultatet av multiplikasjonen.

For eksempel, for å multiplisere 4 x 3, er 3 brikker plassert i 4 små bokser; Så begynner de å telle brikkene til den første boksen, og plasserer dem i den store boksen; Dette gjentas med de 3 boksene. I den sentrale boksen vil de ha: 3 + 3 + 3 + 3 = 12 brikker.

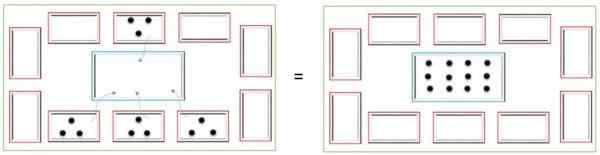
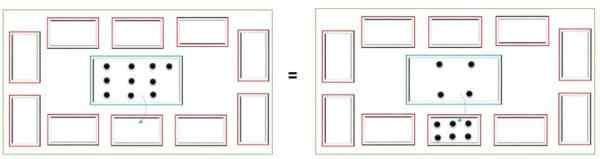
Inndeling

Divisjonen handler om å distribuere en mengde elementer likt. For å dele 16 brikker i 4 små bokser er disse for eksempel plassert i den sentrale boksen, og er distribuert i små bokser på en slik måte at i hver boks er den samme mengden flis igjen.

Til slutt er det mengden brikker hver boks må bestemme resultatet; I dette tilfellet vil hver ha 4 brikker.