Fysisk

elektrisk felt

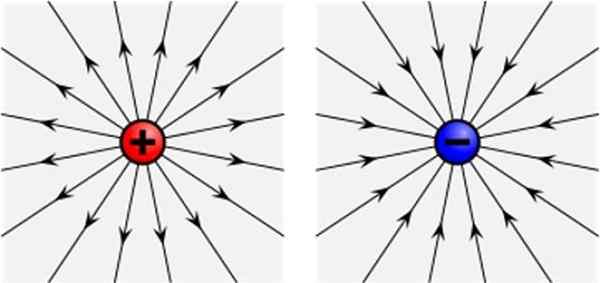
Det elektriske feltet til et positivt (venstre) og negativt (til høyre). Kilde: Wikimedia Commons

Hva er det elektriske feltet?

Han elektrisk felt Det er eiendommen som gjenstandene lastet med påvirkning av det omkringliggende rommet har, som oppfattes av andre elektrisk ladede kropper. Men i motsetning til den elektriske kraften mellom belastninger, avhenger det elektriske feltet bare av belastningen som produserer den.

Michael Faraday (1791-1867), en engelsk fysiker, skapte feltbegrepet ved å observere at enhver elektrisk ladning påvirker plassen som omgir det, slik at den ikke trenger å være i kontakt med en annen belastning slik at samspillet oppstår.

Det er ikke en gang nødvendig at belastningene er i et materielt medium, siden samspillet kan gis i et vakuum.

For å visualisere formen på et elektrisk felt, anta en spesifikk og positiv belastning, kalt +Q, hvis størrelse er så liten at det ikke er nødvendig å ta hensyn til dens dimensjoner. Feltet hun produserer er i stand til å påvirke andre ladninger, for eksempel en annen positiv testpunktbelastning q_enten.

Testbelastningen er plassert på forskjellige steder rundt +Q, og for å være både positiv, kraften som +Q utøver på Q_enten Det er frastøtning.

Tegne kraftkraften på belastningen q_enten På hvert punkt i plassen den okkuperer, og fjerner det, er det et sett med linjer som dukker opp radialt fra belastningen +q (se bildet over til venstre).

Når du gjentar opplevelsen med en negativ belastning - Q, er linjene også radielle, men inngår til - q. I begge tilfeller er linjene tangent til vektorelektrisk felt av belastningen, utadvendt når det er positivt, og innkommende hvis det er negativt.

Formel og enheter

Hvis det i et område med plass er et elektrisk felt OG, En elektrisk ladning Q_enten Erfaring, takk til ham, en styrke gitt av:

Kan tjene deg: Tilfeldig feil: Formel og ligninger, beregning, eksempler, øvelser

F = q_entenOG

Så det:

$\mathbfE=\frac\mathbfF\mathrmq_o$

Den elektriske feltenheten i det internasjonale systemet med enheter er Newton/Coulomb, som er forkortet N/C. Det er også vanlig å uttrykke det elektriske feltet i form av en skalarstørrelse som kalles elektrisk potensial, i hvilket tilfelle feltet for feltet er volt/meter (v/m).

Det elektriske feltet med en punktlig belastning

Felt OG er produsert av noen objekter med belastning q. Gjør prøvebelastningen veldig liten, det vil si å lage q_enten har en tendens til 0, vektoren OG er:

$\mathbfE=\lim_q_o\rightarrow 0\frac\mathbfF_o\mathrmq_o$ Med F_entenstyrken mellom q og q_enten.

Intensjonen når du tar grensen er å gjøre forsøksbelastningen liten nok til at feltet ikke endrer den som vil beregne.

Hvis det er en punktlig belastning, i henhold til Coulombs lov, styrken mellom anklagene Q og Q_enten, Begge atskilt en avstand R, er gitt av:

$\mathbfF_o=k\fracq\cdot q_or^2\hatr$ I denne ligningen er k den elektrostatiske konstanten og enhetsvektoren i retning av linjen som forener Q og Q og Q og Q_entener: $\hatr$

Erstatte dette uttrykket i definisjonen av felt, oppnås det:

$\mathbfE =\lim_q_o\rightarrow 0\frack\fracqq_or^2q_o\hatr=k\fracqr^2\hatr$ Slik at feltet OG, Produsert av den punktlige belastningen Q på punkt P, er:

$\mathbfE =\frackqr^2\hatr$ Dermed, OG Det avhenger ikke av prøvebelastningen, men av belastningen som produserer den. De omfanget av feltet er direkte proporsjonal med størrelsen på belastningen, og omvendt proporsjonal med kvadratet av avstanden mellom belastningen og punktet P.

Og som sagt i begynnelsen, adresse Fra feltet er det radielt og retningen er utgående til belastningen når den er positiv, og innkommende når den er negativ.

Elektrisk feltintensitet

Det elektriske feltet er vektor, og intensiteten refererer til modulen eller størrelsen, som er betegnet uten fet skrift. For en punktlig belastning er intensiteten til det elektriske feltet ganske enkelt:

Kan tjene deg: Overfladisk utvidelse: Formel, koeffisienter og eksempler

$E =\frackqr^2$ Og for å være modulen til et beløp, er det alltid positivt.

For eksempel intensiteten til det elektriske feltet produsert av en belastning Q = - 4.3 μC (μC lyder “Microcoulomb” og tilsvarer milliondelen av en Coulomb), i en avstand på 2 cm fra belastningen, er det:

$E =\frac9\times 10^9\times 4.3\times 10^-6\left (2\times 10^-2 \right )^2\: \fracNC$

Merk at avstanden på 2 cm ble meter, multipliserer med kraften 10⁻², Siden den elektrostatiske konstanten er i enheter hvis. Og selv om belastningen er negativ, er intensiteten på feltet den produserer alltid positiv, men den elektriske feltvektoren er innkommende for belastningen, som tidligere forklart.

Eksempler på elektrisk felt

1. Elektrisk felt med diskret fordeling av belastninger

Et sett med spesifikke kostnader kalles Diskret belastningsfordeling. I så fall beregnes det resulterende elektriske feltet ved punkt P ved å bruke Superposisjonsprinsipp, som er sumvektoren til feltet som hver av belastningene produserer i P:

OG_nett = OG₁+ OG₂+ OG₃+..

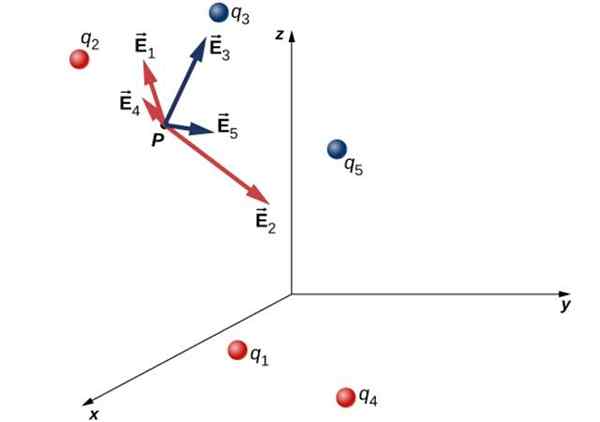
Følgende bilde viser en distribusjon sammensatt av fem spesifikke belastninger og det elektriske feltet som hver produserer på punkt P:

Elektrisk felt på punkt P, på grunn av en diskret fordeling av belastninger

Lastene q₃ og q₅ De er negative og feltet de produserer er innkommende for dem. De skiller seg ut i blått.
For sin del, belastningene q₁, q₂og q₄De er positive, og skaper et fremtredende felt i rødt.

2. Elektrisk felt med kontinuerlig fordeling av belastninger

En kontinuerlig belastningsfordeling består av et utvidet objekt, elektrisk lastet, for eksempel den som er vist i følgende figur. Siden objektet har betydelige dimensjoner, er feltet som en del av kroppen produserer i P betydelig forskjellig fra den som produserer en annen ytterligere (eller nærmest) av P.

Kan tjene deg: Kirchhoff -lover

Anta at en liten elektrisk ladning av nevnte objekt er tatt, kalt DQ og antatt positivt, som i P i P i P et lite bidrag til det totale elektriske feltet. Dette bidraget er en differensial av den elektriske feltvektoren DOG.

Siden DQ -belastningen er veldig liten, er feltet som en punktlig belastning, slik at ligningen kan brukes før sett:

$d\mathbfE=k\fracdqr^2\hatr$

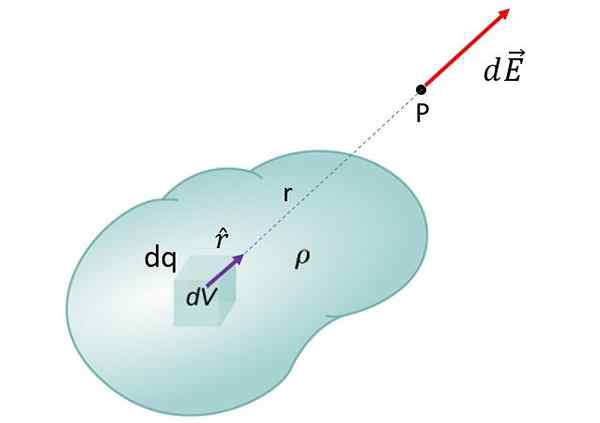For å beregne det elektriske feltet til et utvidet objekt, er det integrert over alt volumet. Lastetettheten (belastning per volum enhet) er betegnet som ρ

For å få det totale feltet til objektet på punkt P, blir bidragene til alle DQ som kan tas på objektet lagt til. Dette fører til integralen:

$\mathbfE=\int_Volumen^k\fracdqr^2\hatr$

Trening løst

En punktlig belastning q = 2.0 × 10⁻⁸ C er plassert på et punkt P i et elektrisk felt, der det opplever en stigende styrke i styrken 4.0 × 10⁻⁶ N. Regne ut:

a) Det elektriske feltet i P

b) Kraften på en belastning q = −1.0 × 10⁻⁸ C Ligger i P.

Løsning på

Være størrelsen på det elektriske feltet som belastningen er plassert i. I kraft av dette feltet opplever denne belastningen den oppadgående styrkenes kraft F, slik at:

F = q ∙ e

Så:

E = f /q = 4.0 × 10^-6 N/ 2.0 × 10^-8 C = 200 N/C.

Å være positiv byrden, kraft og felt har samme retning og mening.

Løsning b

Størrelsen på kraften som virker på det som er:

$F=\left |q \right | \cdot E=\left |-1.0\times 10^-8 \right | \cdot 200\: N=2.0\times 10^-6 \: N$

Når denne byrden er negativ, har kraft og felt samme retning, men motsatte sanser.

Referanser

Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 2. Mc Graw Hill.
Felt- og elektrisk potensial for en punktlig belastning. Hentet fra: SC.Ehu.er.
Resnick, r. (1999). Fysisk. Vol. 1. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V.
Sears, z. (2016). Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1. Pearson.
Universitetsfysikk. Elektrisk felt. Vol. 2. Hentet fra: OpenStax.org.