Effektiv kjernefysisk belastning

Hva er effektiv kjernefysisk belastning?

De effektiv kjernefysisk belastning (representert som z_Eff Og i noen tilfeller som z^*) Det er netto kjernefysisk belastning som et elektron opplever når det er i et polyhelectronic -atom (det vil si at det har mer enn ett elektron).

På en mer presis måte er det den elektriske ladningen som vil ha kjernen i et hypotetisk atom som er i stand til å tiltrekke det eneste elektronet med samme kraft som kjernen i det virkelige atomet tiltrekker det samme elektronet i nærvær av alle andre elektroner.

Det er en korrigert kjernefysisk belastning som tar hensyn. Denne reduserte belastningen forklarer hvorfor de ytterste elektronene i et polyhelectronic -atom er svakt knyttet til kjernen enn indre elektroner.

Effektiv kjernefysisk belastning er et begrep av stor betydning i kjemi, siden det lar oss forstå den periodiske tendensen til mange egenskaper som atomradius, ionradius, elektronegativitet, ioniseringsenergier og mer.

Hvorfor eksisterer den effektive kjernefysiske belastningen?

Den effektive kjernefysiske belastningen oppstår fra to fenomener:

• Skjermingseffekten av elektroner på polyhelektroniske atomer.
• Elektrostatisk frastøtning blant elektroner fordi alle har samme elektriske ladning.

Han Skjermingseffekt Den består av et slags skjold dannet av de indre elektronene til et atom som dekker kjernen. Dette får de ytterste elektronene til å "føle" en lavere attraksjon fra kjernen enn de ville følt hvis de andre elektronene ikke var til stede.

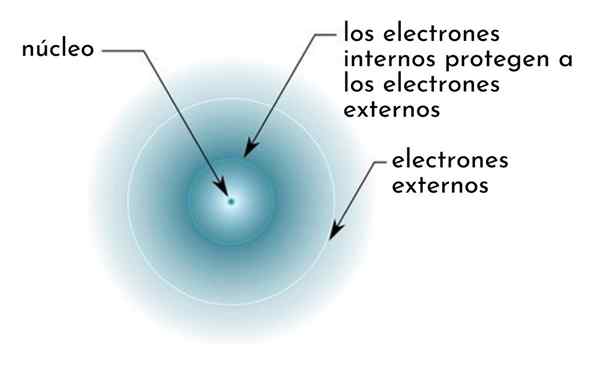Figur som skjematisk viser indre elektroner som fungerer som en skjerm som beskytter de ytre elektronene for attraksjonen til kjernen

For eksempel er kjernefysisk belastning på natriumatom +11 (dets atomnummer er z = 11), men det eneste elektronet i Valencia som det besitter, føler faktisk at tiltrekningen av en belastning på bare +2,2.

Kan tjene deg: natriumbenzoate: struktur, egenskaper, bruksområder og risikoer

Med andre ord får beskyttelsen av de andre 10 indre elektronene Valencia -elektronet i natrium til å føle en kraft med kjernefysisk attraksjon på bare den femte av det som skal være.

I tillegg til skjermingseffekten, frastøtning mellom elektronene (som har samme elektriske ladning) bidrar også til å motvirke kapasiteten til kjernen til å tiltrekke ytre elektroner. Det vil si at denne frastøtningen også bidrar til å redusere effektiv kjernefysisk belastning.

Viktige kjennetegn ved effektiv kjernefysisk belastning

Det skal bemerkes at skjermingseffekten som er ansvarlig for å redusere effektiv kjernefysisk belastning, bare påvirker elektroner som er i samme energinivå eller i de øvre lagene, men ikke de mest indre elektronene. I tillegg er effekten ikke den samme for elektroner som finnes i atombaner S og P enn de som finnes i orbitaler d og f.

Av denne grunn føles hvert elektronsett av hvert lag eller energinivå en annen effektiv kjernefysisk belastning. Dette har viktige implikasjoner angående de kjemiske egenskapene til de forskjellige elementene.

Periodisk trend med effektiv kjernefysisk belastning

Over en periode

Elektroner som ligger på samme energinivå er mindre skjerming enn de som finnes i lavere energinivå.

På grunn av dette øker ikke skjermingseffekten betydelig når vi beveger oss over en periode, men den virkelige kjernefysiske belastningen gjør. Av denne grunn er den effektive kjernefysiske belastningen øker fra venstre til høyre i det periodiske bordet.

Gjennom en gruppe

På den annen side, når vi går fra en periode til en annen i samme gruppe (det vil si når vi beveger oss ned langs en gruppe), tilsettes hele lag med veldig beskyttelse av indre elektroner. Dette gjør at den effektive kjernefysiske belastningen avtar fra topp til bunn eller, hva er det samme, Øk nedenfra og opp.

Kan tjene deg: Ayaroína

Effektiv atombelastningsformel

Effektiv kjernefysisk belastning kan beregnes ved hjelp av en veldig enkel semi -tidsligning som tar hensyn til den faktiske verdien av atombelastningen (gitt av atomnummeret, z) og et begrep som kalles konstant skjerming. Sistnevnte omfatter effekten av tilstedeværelsen av andre elektroner i en.

Ligningen er gitt av:

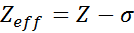
Hvor Z er atomnummeret og σ (gresk bokstav Sigma) representerer skjermkonstanten, som avhenger av den elektroniske konfigurasjonen.

Slater regler

Skjermingskonstanten kan estimeres fra et system kjent som Slater -reglene. Disse reglene tillater beregning av skjoldkonstanten til et elektron ved å legge til bidragene fra de andre elektronene til nevnte skjerming konstant. Disse reglene kan oppsummeres som følger:

• Ethvert elektron som er på samme energinivå (nivå n₀) Gir et beløp på 0,35 til skjermingskonstanten, med mindre begge er på nivå 1, i hvilket tilfelle den gir 0,30.
• Hvert elektron som er på umiddelbart tidligere nivå (på nivå n₀-1) I en orbital S eller P bringer det 0,85; På den annen side, hvis det er i en orbital d eller f, bidrar det 1.
• Alle andre elektroner som er på lavere energinivå (n₀-2, n₀-3, etc.), bidra 1 til skjermingskonstanten.

Eksempel på effektiv beregning av kjernefysisk belastning

Valencia -elektron av natriumatom

Den elektroniske konfigurasjonen av natriumatom er 1s²2s²2 s⁶3s¹. Det vil si at hvis vi vil beregne den effektive kjernefysiske belastningen som Valencia -elektronet føler (elektron 3S¹), må vi legge til bidragene fra de andre 10 elektronene etter slaterreglene.

Kan tjene deg: jernoksid (ii): struktur, nomenklatur, egenskaper, bruk

Hvordan beregner vi 3S elektronskjold konstant¹ (n₀= 3) Og dette er alene i Valencia -laget, det er ingen andre elektroner på samme energinivå.

Det umiddelbart forrige nivået er n₀-1 = 2, der det er 8 elektroner i orbital S eller P som bidrar med 0,85 hver, og det er ingen elektroner i orbitaler d eller f.

Til slutt er det eneste nivået lavere enn 2 n = 1, der det bare er 2 elektroner. Alt dette er oppsummert i følgende tabell:

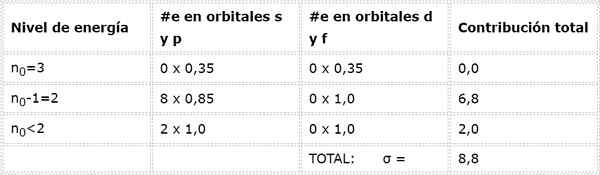
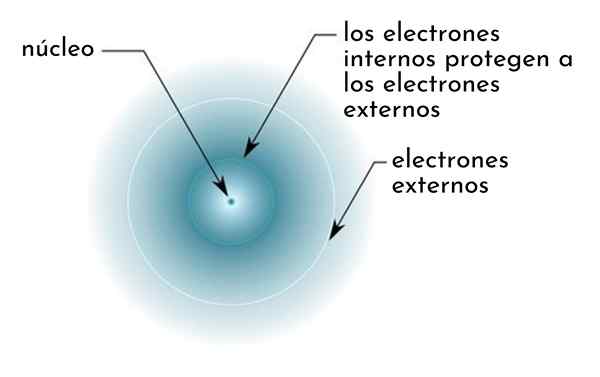
Som det kan sees, gir de indre elektronene i natrium en skjoldkonstant på 8,8, så den effektive kjernefysiske belastningen som elektronet føler 3S¹ er:

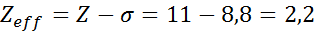
Arsen Valencia -elektroner

Den arsen elektroniske konfigurasjonen er 1s²2s²2 s⁶3s²3p⁶3d¹⁰4s²4p³. Valencia -laget er lag 4 (n₀= 4) som har 5 elektroner: (4s²4p³). I dette tilfellet vil hver av disse 5 elektronene føle effekten av de andre 4 som er i samme lag og den av de andre 28 indre elektronene som vist i tabellen:

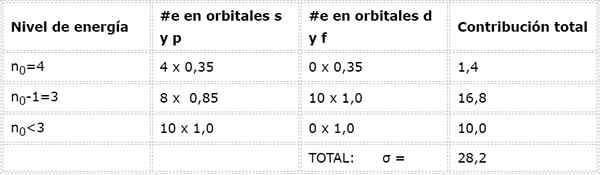
Derfor er den effektive kjernefysiske belastningen som de arsen Valencia -elektronene føler: