Enhetlige celleegenskaper, rød konstant og typer

De Unitary Cell Det er et tenkt rom eller region som representerer minimumsuttrykk for en helhet; At i tilfelle av kjemi, ville hele være en krystall sammensatt av atomer, ioner eller molekyler, som er bestilt etter et strukturelt mønster.

I dagliglivet kan du finne eksempler som legemliggjør dette konseptet. For dette er det nødvendig å ta hensyn til objekter eller overflater som viser en viss repeterende rekkefølge av elementene. Noen mosaikker, bas -relief, håndverk.

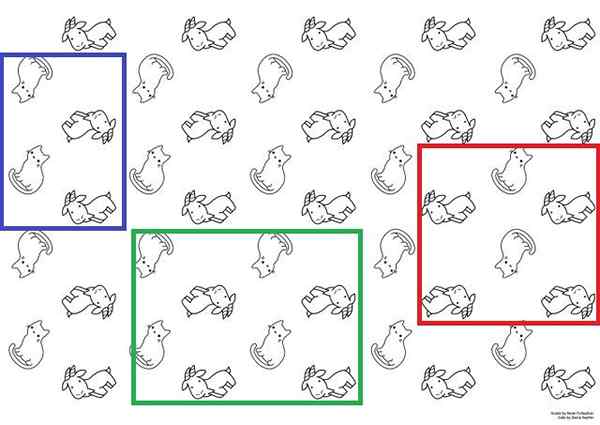
Enhetlige celler på katt- og geitepapir. Kilde: Hanna Petruschat (WMDE) [CC BY-SA 4.0 (https: // creativecommons.Org/lisenser/by-SA/4.0)].

For å illustrere det tydeligere, har du det overlegne bildet som kan brukes som et billedpapir. I den vises katter og geiter med to alternative sanser; Katter er føtter eller hode, og geitene ser opp eller ned.

Disse kattene og geitene etablerer en repeterende strukturell sekvens. For å bygge alt papiret, ville det være nok å reprodusere den enhetlige cellen av overflaten et tilstrekkelig antall ganger, ved hjelp av translasjonsbevegelser.

De mulige enhetscellene er representert med de blå, grønne og røde boksene. Noen av disse tre kan brukes til å skaffe papiret; Men det er nødvendig å bevege dem som er tenkt langs overflaten for å finne ut om de reproduserer den samme sekvensen som er observert på bildet.

Fra og med den røde boksen vil det bli satt pris på at hvis tre kolonner (av katter og geiter) ble flyttet til venstre, ville to geiter ikke lenger vises i den nedre delen, men bare en. Derfor vil det føre til en annen sekvens og kan ikke betraktes som en enhetscelle.

Selv om de forestiller seg de to boksene, blå og grønne, ville den samme papirsekvensen oppnås. Begge er enhetsceller; Imidlertid adlyder den blå boksen definisjonen mer, siden den er mindre enn den grønne boksen.

[TOC]

Enhetscelleegenskaper

Hans egen definisjon, i tillegg til det nylig forklarte eksemplet, tydeliggjør flere av dets egenskaper:

-Hvis de beveger seg i verdensrommet, uavhengig av retning, vil det komplette faste eller glasset oppnås. Dette er fordi de, som nevnt med katter og geiter, reproduserer den strukturelle sekvensen; som er lik den romlige fordelingen av repeterende enheter.

-De må være så små som mulig (eller okkupere lite volum) sammenlignet med andre mulige cellealternativer.

Kan tjene deg: metylmalonsyre: struktur, egenskaper, syntese, bruk

-De er, vanlige, symmetriske. På samme måte gjenspeiles symmetrien bokstavelig talt i krystallene til forbindelsen; Hvis enhetscellen til et salt er kubikk, vil krystallene være kubikk. Imidlertid er det krystallinske strukturer beskrevet med enhetsceller med forvrengte geometrier.

-De inneholder de repeterende enhetene, som kan erstattes av punkter, som igjen tre -dimensjonalt hva som er kjent som en reticle. I det forrige eksemplet representerer katter og geiter de retikulære punktene, sett fra et høyere plan; det vil si to dimensjoner.

Antall repeterende enheter

De repeterende enhetene eller retikulære punktene til enhetscellene opprettholder den samme andelen av de faste partiklene.

Hvis antallet katter og geiter telles inne i den blå boksen, vil det være to katter og geiter. Det samme gjelder den grønne boksen, og med den røde boksen også (selv om det allerede er kjent at det ikke er en enhetscelle).

Anta for eksempel at katter og geiter er henholdsvis atomer G og C (en merkelig dyresveising). Ettersom andelen mellom G og C er 2: 2 eller 1: 1 i den blå boksen, kan det forventes, uten feil, at det faste stoffet vil ha GC (eller CG) formelen.

Når det faste stoffet har mer eller mindre kompakte strukturer, som med salter, metaller, oksider, sulfider og legeringer, er det i enhetscellene ingen hele repeterende enheter; Det vil si at det er deler eller deler av dem, som legger opp til en eller to enheter.

Dette er ikke tilfelle for GC. Hvis den blå boksen "ville starte" til katter og geiter i to (1/2G og 1/2C) eller fire deler (1/4G og 1/4C). I de neste seksjonene vil det sees at i disse enhetscellene er retikulære punktene praktisk delt på dette og andre måter.

Hvilke nettverkskonstanter definerer en enhetscelle?

De enhetlige cellene i GC -eksemplet er to -dimensjonale; Dette gjelder imidlertid ikke i de virkelige modellene som vurderer de tre dimensjonene. Dermed blir boksene eller parallellogrammer transformert til parallelepípedos. Nå tar begrepet "celle" større sans.

Dimensjonene til disse cellene eller parallellepipedene avhenger av hvor lenge deres respektive sider og vinkler er.

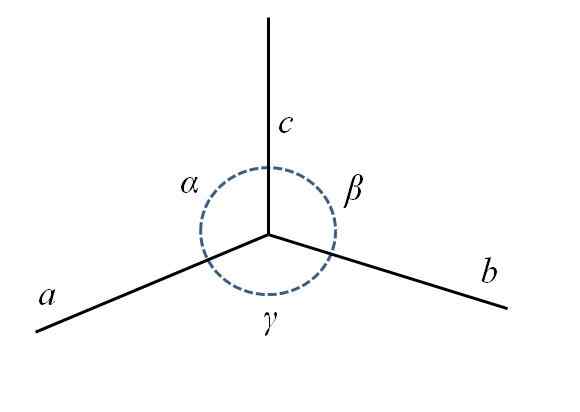
I det nedre bildet har du det nedre bakre hjørnet av parallellpiped, sammensatt av sidene til, b og c, og vinklene α, β og γ.

Parametere for en enhetscelle. Kilde: Gabriel Bolívar.

Som du kan se, til er litt lengre enn b og c. I sentrum har du en sirkel med en stiplet linje for å indikere vinklene α, β og γ, mellom Ac, CB og ba, henholdsvis. For hver enhetscelle har disse parametrene konstante verdier, og definerer symmetrien og resten av glasset.

Kan tjene deg: kalsiumperoksyd (CAO2): egenskaper, risikoer og bruksområder

Påføring av litt fantasi igjen, ville bildeparametrene definere en celle som ligner på en strukket kube i kanten til. Dermed oppstår enhetsceller med forskjellige lengder og vinkler på kantene, som også kan klassifiseres i forskjellige typer.

Folkens

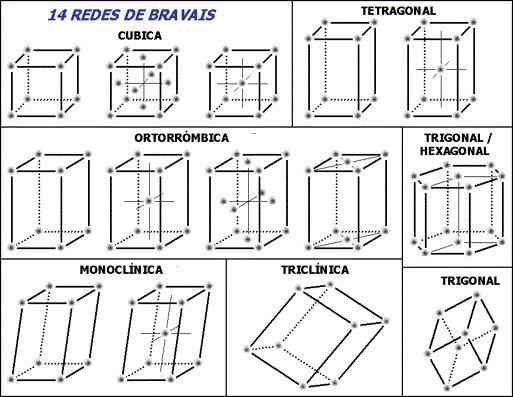
De 14 Bravais -nettverkene og de syv grunnleggende krystallinske systemene. Kilde: Den originale opplasteren var angre på portugisisk Wikipedia. [CC By-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/]]

Merk for å starte de stiplede linjene inne i enhetscellene: de indikerer den nedre bakvinkelen, som forklart. Følgende spørsmål kan stilles, hvor er retikulære punkter eller repeterende enheter? Selv om de gir feil inntrykk av at cellene er tomme, ligger svaret.

Disse cellene genereres eller velger på en slik måte at de repeterende enhetene i deres hjørner er plassert (grå punkter på bildet). Avhengig av verdiene til parametrene som er etablert i forrige seksjon, konstant for hver enhetscelle, er syv krystallinske systemer avledet.

Hvert krystallinsk system har sin egen enhetlige celle; Den andre definerer den første. I det øvre bildet er det syv bokser, tilsvarende de syv krystallinske systemene; eller litt mer sammendrag, krystallinske nettverk. Dermed tilsvarer en kubisk enhetscelle for eksempel et av de krystallinske systemene som definerer et kubikk krystallinsk nettverk.

I følge bildet er de krystallinske systemene eller nettverkene:

-Kubikk

-Tetragonal

-Ortorrombica

-Sekskantet

-Monoklinisk

-Triclinic

-Trigonal

Og innenfor disse krystallinske systemene som utgjør de fjorten garnene i Bravais; at de blant alle krystallinske nettverk er de mest grunnleggende.

Kubikk

I en kube er alle sider og vinkler de samme. Derfor blir følgende oppfylt i denne enhetscellen:

til = b = c

α = β = γ = 90º

Det er tre cubiske enhetsceller: enkle eller primitive, sentrert på kroppen (BCC), og sentrert på ansikter (FCC). Forskjellene ligger i hvordan punktene (atomer, ioner eller molekyler) og i antall av dem er distribuert.

Hvilken av disse cellene er de mest kompakte? Det hvis volum er mer okkupert av punkter: kubikk sentrert på ansiktene. Merk at hvis vi erstatter punktene med begynnelsen av kattene og geitene, ville de ikke være begrenset til en enkelt celle; De ville høre til og bli delt av flere. Igjen, det ville være deler av G eller C.

Det kan tjene deg: hydrokoloid

Antall enheter

Hvis katter eller geiter var i toppunktene, ville de bli delt av 8 enhetsceller; Det vil si at hver celle ville ha 1/8 G eller C. Sammen eller forestill deg 8 terninger, i to søyler med to rader hver, for å visualisere det.

Hvis katter eller geiter var i ansiktet, ville de bare bli delt av 2 enhetsceller. For å se det, er det nok å samle to terninger.

På den annen side, hvis katten eller geiten var i midten av kuben, ville de bare tilhøre en enkelt enhetlig celle; Det samme skjer med boksene til hovedbildet, da konseptet ble adressert.

Sa da ovenstående, innenfor en enkel kubikkcelle en Enhet eller retikulært punkt, siden det har 8 hjørner (1/8 x 8 = 1). For den kubiske cellen sentrert i kroppen du har: 8 hjørner, som er lik et atom, og et punkt eller enhet i sentrum; Derfor er det to enheter.

Og for den kubiske cellen sentrert på ansiktene du har: 8 hjørner (1) og seks ansikter, hvor halvparten av hvert punkt eller enhet deles (1/2 x 6 = 3); Derfor har det fire enheter.

Tetragonal

Lignende kommentarer kan gjøres med hensyn til enhetscellen for det tetragonale systemet. Dens strukturelle parametere er som følger:

til = b ≠ c

α = β = γ = 90º

Ortorrombica

Parametrene for den ortorrombiske cellen er:

til ≠ b ≠ c

α = β = γ = 90º

Monoklinisk

Parametrene for monoklinisk celle er:

til ≠ b ≠ c

α = γ = 90º; β ≠ 90º

Triclinic

Parametrene for den trikliniske cellen er:

til ≠ b ≠ c

α ≠ β ≠ γ ≠ 90º

Sekskantet

Parametrene for den sekskantede cellen er:

til = b ≠ c

α = β = 90º; γ ≠ 120º

Faktisk utgjør cellen den tredje delen av et sekskantet prisme.

Trigonal

Og til slutt er parametrene for den trigonale cellen:

til = b = c

α = β = γ ≠ 90º

Referanser

1. Whitten, Davis, Peck & Stanley. (2008). Kjemi. (8. utg.). Cengage Learning P 474-477.
2. Shiver & Atkins. (2008). Uorganisk kjemi. (Fjerde utgave). Mc Graw Hill.
3. Wikipedia. (2019). Primitiv celle. Hentet fra: i.Wikipedia.org
4. Bryan Stephanie. (2019). Enhetscelle: Latice -parametere og kubiske strukturer. Studere. Gjenopprettet fra: Studie.com
5. Akademisk ressurssenter. (s.F.). Krystallstrukturer. [PDF]. Illinois Institute of Technology. Hentet fra: Web.IIT.Edu
6. Belford Robert. (7. februar 2019). Krystalllatice og enhetsceller. Kjemi librettexts. Gjenopprettet fra: Chem.Librettexts.org