Tyngdekraftsegenskaper, beregning, eksempler

Han Gravity Center av en målbar størrelse kropp er punktet der vekten anses å bli brukt. Det er derfor et av de primære konseptene med statisk.

Den første tilnærmingen i elementære fysikkproblemer er å anta at ethvert objekt oppfører seg som en spesifikk masse, det vil si at den mangler dimensjoner og hele massen er konsentrert på et enkelt punkt. Dette er gyldig for en boks, en bil, en planet eller en subatomisk partikkel. Denne modellen er kjent som partikkelmodell.

Figur 1. I høyden hopp, idrettsutøveren fikser dem slik at tyngdepunktet er utenfor kroppen. Kilde: Pixabay

Naturligvis er dette en tilnærming, som gir veldig gode resultater for mange applikasjoner. Det er ikke en lett oppgave å vurdere den individuelle oppførselen til tusenvis og millioner av partikler som ethvert objekt kan inneholde.

Imidlertid bør de virkelige dimensjonene til ting tas med i betraktningen hvis du vil. Siden vi vanligvis er i nærheten av jorden, er den alltid nåværende kraften på ethvert legeme nettopp vekten.

[TOC]

Hensyn til å finne tyngdepunktet 

Hvis kroppsstørrelsen skal tas i betraktning, hvor vekten blir brukt spesifikt? Når du har et kontinuerlig objekt vilkårlig, er vekten en Distribuert kraft mellom hver av dens konstituerende partikler.

La disse partiklene m₁, m₂, m₃... hver av dem opplever dens tilsvarende gravitasjonskraft m₁g, m₂g, m₃G ..., alle parallelle. Dette er slik, siden jordens gravitasjonsfelt anses som konstant i de aller fleste tilfeller, med tanke på at gjenstander er små sammenlignet med størrelsen på planeten og er nær overflaten.

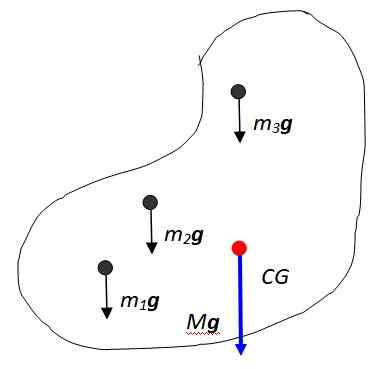Figur 2. Vekten til objektet er en distribuert masse. Kilde: Selvlaget.

Vektorsummen av disse kreftene resulterer i objektets vekt, brukt på det punktet som kalles tyngdepunktet betegnet i figuren som CG, som deretter sammenfaller med Massesenter. Massesenteret på sin side er poenget der hele massen kan betraktes som konsentrert.

Den resulterende vekten har størrelse Mg hvor M Det er den totale massen til objektet, og selvfølgelig er den rettet vertikalt mot jordens sentrum. Sumorisk notasjon er nyttig for å uttrykke kroppens totale kropp:

Symmetriske og homogene gjenstander, som tilsvarer at deres tetthet er ensartet, har sitt tyngdepunkt i det geometriske sentrum: kuber, parallellepiped, ringer, dekk eller sfærer.

Tyngdepunktet samsvarer ikke alltid med et materielt punkt. For eksempel er CG for en bøyle i sitt geometriske sentrum, der det ikke er noen deig i seg selv. Likevel, hvis du vil analysere kreftene som virker på en bøyle, må vekten påføres dette presise punktet.

I hvilke tilfeller der objektet er vilkårlig, hvis det er homogent, kan massesenteret fremdeles beregnes ved å finne centroid o baricentro av figuren.

Kan tjene deg: Merkur (planet)

Hvordan beregnes tyngdepunktet?

I prinsippet hvis tyngdepunktet (CG) og massesenteret (CM) sammenfaller når gravitasjonsfeltet er ensartet, kan CM beregnes og på den påfør vekten.

Tenk på to tilfeller: den første er en der massedistribusjonen er diskret; Det vil si at du kan telle hver masse som danner systemet og tilordne et nummer I, som det ble gjort i forrige eksempel.

Koordinatene til massesenteret for en diskret massefordeling er: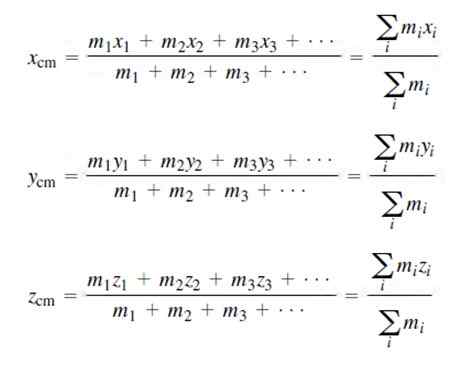

Naturligvis tilsvarer summen av alle massene den totale massen av M -systemet, som angitt ovenfor.

De tre ligningene reduseres til en kompakt form når man vurderer vektoren r_CM o Posisjonsvektor i massesenteret:

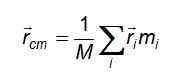
Og i tilfelle en kontinuerlig massefordeling, der partiklene er av differensialstørrelse og ikke kan skilles ut for å telle dem, erstattes summen av et integral som er laget om volumet okkupert av det aktuelle objektet:

Hvor r Det er posisjonsvektoren til en differensialmasse DM Og definisjonen av massetetthet for å uttrykke massedifferensialet er blitt gjort DM inneholdt i en volumdifferensial Dv:

Objektets tetthet kan være konstant, i hvilket tilfelle det kommer ut av integralen, eller å være en funksjon av de romlige koordinatene, og vi må vite dets avhengighet av (x, y, z) for å løse integralen.

Egenskaper

Noen viktige hensyn til massesenteret er følgende:

- Selv om det er nødvendig med et referansesystem for å etablere posisjoner, er ikke massesenteret avhengig av valget som er gjort av systemet, siden det er en egenskap til objektet.

- Når objektet har en akse eller et symmetri -plan, er massesenteret på nevnte akse eller plan. Dra nytte av denne omstendigheten sparer beregningstid.

- Alle eksterne krefter som virker på objektet kan brukes på massesenteret. Å følge sporet av dette punktet gir en global ide om bevegelsen av objektet og letter arbeidet med å studere dets oppførsel.

-Finne tyngdepunktet i en kropp i statisk balanse

Anta at kroppen til forrige figur er i statisk balanse er.

Figur 3. Ordning for å beregne vekten av vekt med hensyn til punkt eller.

Momentet for netto torsjon med hensyn til O, ifølge figur 3 er: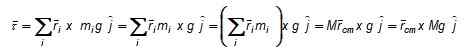En kraft F påført vertikalt opp i tyngdepunktet (eller også over eller under, på aksen som passerer gjennom den) ville gi en motsatt torsjon som ville forhindre rotasjon av objektet og opprettholde rotasjonsbalansen. Størrelsen på F er valgt slik at objektet ikke overføres heller, og på denne måten vil vi ha det i statisk likevekt.

Kan tjene deg: bølgende optikk

-Løst eksempel

En tynn stang med ensartet materiale har en lengde på 6 m og veier 30 N. På slutten er en 50 n vest og en annen på 20 N i høyre ende hengt. Finn: a) Størrelsen på den stigende kraften som er nødvendig for å opprettholde balansen i baren, b) Settets tyngdepunkt.

Løsning

Krefter -diagrammet er vist i følgende figur. Stangens vekt påføres i tyngdepunktet, som sammenfaller med dets geometriske sentrum. Den eneste dimensjonen av baren som tas i betraktning er dens lengde, siden uttalelsen informerer om at den er tynn.

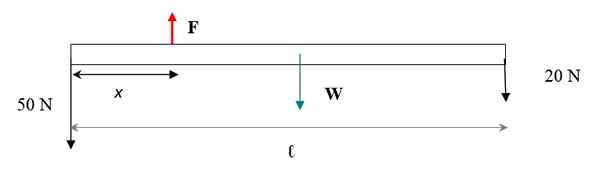Figur 4. Pàra la barra diagram.

For at BAR + vektsystemet skal forbli i oversettelsesbalanse, må summen av kreftene være null. Kreftene er vertikale, hvis vi vurderer med et skilt + og ned med et tegn - da:

F- 50- 20-30 n = 0

F = 100 n

Denne styrken garanterer oversettelsesbalansen. Å ta øyeblikkene av torsjon av alle krefter angående en akse som går gjennom venstre ende av systemet og anvende definisjonen:

t = r x f

Momentene til alle disse kreftene med hensyn til det valgte punktet er vinkelrett på stangens plan:

t_F = xf = 100x

t_W = -(l/2) mg = -3m . 30 n = -90 n.m

t₁ = 0 (Siden kraften på 50 N passerer gjennom den valgte svingaksen og ikke trener moment)

t₂ = -Lf₂ = 6 m . 20 n = -120 n.m

Derfor:

100 x -90 -120 n.m = 0

x = 2.10 m

Tyngdepunktet til stangstangen + vekter er plassert på 2.10 meter fra venstre ende av baren.

Forskjell med massesenteret

Tyngdepunktet sammenfaller med massesenteret, som indikert, så lenge landets gravitasjonsfelt er konstant for at alle gjenstandens punkter skal vurderes. Gravitasjonsfeltet på jorden er ikke noe annet enn den kjente og kjente verdien av G = 9.8 m/s² rettet vertikalt ned.

Selv om verdien av G opplever variasjoner med breddegrad og høyde, påvirker de vanligvis ikke objekter som de fleste ganger blir behandlet. Veldig annerledes ville være hvis det regnes som et stort legeme i nærheten av jorden, for eksempel en asteroide som ville nær planeten.

Asteroiden har sitt eget massesenter, men tyngdepunktet trenger ikke lenger å sammenfalle med dette, siden g Det vil sannsynligvis oppleve betydelige variasjoner i størrelsesorden, gitt størrelsen på asteroiden og at vektene til hver partikkel kanskje ikke er parallell.

En annen grunnleggende forskjell er at massesenteret er uavhengig av om det er en kraft som kalles påført vekt på objektet eller ikke. Det er en iboende egenskap til objektet som avslører hvordan massen er fordelt i forhold til dens geometri.

Kan tjene deg: Hva er den dielektriske konstanten?

Massesenteret eksisterer både hvis det blir brukt vekt som om ikke. Og ligger i samme posisjon, selv om objektet overføres til en annen planet der gravitasjonsfeltet er forskjellig.

På den annen side er tyngdepunktet tydelig knyttet til påføring av vekt, som vi har kunnet sette pris på gjennom de forrige avsnittene.

Tyngdepunkteksempler

Tyngdepunkt for uregelmessige gjenstander

Det er veldig enkelt å finne ut hvor tyngdepunktet til en uregelmessig gjenstand er som en kopp. Først er den suspendert fra et hvilket som helst punkt og derfra er det tegnet en vertikal linje (i figur 5 er det fuchsia -linjen i venstre bilde).

Da er den suspendert fra et annet punkt og en ny vertikal (turkis linje i riktig bilde) trekkes. Krysset mellom begge linjer er tyngdepunktet i koppen.

Figur 5 . CG plassering av en kopp. Kilde: Modified Pixabay.

Balanse av objekter

La oss analysere stabiliteten til en lastebil som sirkulerer langs veien. Når tyngdepunktet er over basen av lastebilen, vil den ikke helle. Bildet til venstre er den mest stabile posisjonen.

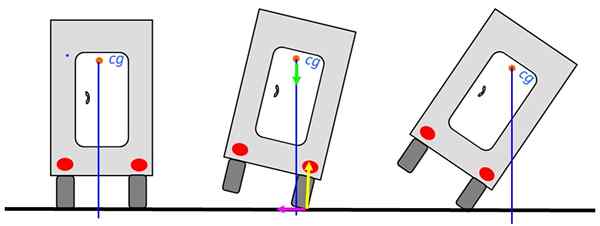Figur 6. Lastebilbalanse. Kilde: Selvlaget.

Selv når lastebilen lener seg til høyre, kan tilbake til den stabile likevektsposisjonen, som på tegningen av mediet, fordi vertikalen fremdeles passerer gjennom basen. Imidlertid når denne linjen passerer utenfor lastebilen vil snu.

Diagrammet viser kreftene på støttepunktet: det normale i gult, vekten i grønt og den statiske friksjonen til venstre i fuchsia. Normal og rubb. Derfor vil de ikke bidra til å dumpe lastebilen.

Vekten gjenstår, som trener et øyeblikk av torsjon, heldigvis i anti -Horary Sense og som har en tendens til å vende tilbake til lastebilen til likevektsposisjonen. Merk at den vertikale linjen passerer gjennom støtteflaten, som er dekket.

Når lastebilen er i posisjonen til den ekstreme høyre, endres tid for torsjon av vekt og blir i en anspent retning. Ikke å være i stand til å bli motvirket på et annet tidspunkt, vil lastebilen strømme.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.  247-253.
2. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. ... Ed Prentice Hall. 229-238.
3. Resnick, r. (1999). Fysisk. Vol. 1. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V. 331-341.
4. Rex, a. 2011. Fundamentals of Physics. Pearson.146-155.
5. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.340-346.