Elastiske sjokk i en dimensjon, spesielle tilfeller, øvelser

De Elastiske sjokk o Elastiske kollisjoner består av korte, men intense interaksjoner mellom objekter, der både bevegelsesmengden og kinetisk energi er bevart. Choques er veldig hyppige hendelser i naturen: fra subatomiske partikler til galakser, som passerer gjennom biljardkuler og sjokkbiler i attraksjonsparker, alle er gjenstander som er i stand til å kollidere.

Under en kollisjon eller sjokk er samhandlingskreftene mellom objekter veldig intense, mye mer enn de som kan handle eksternt. På denne måten kan det bekreftes at partiklene under kollisjonen danner et isolert system.

Kollisjoner mellom biljardkuler kan betraktes som elastiske. Kilde: Pixabay.

I dette tilfellet er det oppfylt at:

Hvor P Det er vektormengden, hvis størrelse er Mv (Hastighetsmasse). Hvis derivatet av P er null, det betyr det P det er konstant. Og dette betyr at det ikke varierer, at det er bevart. Derfor kan vi bekrefte det:

P_enten = S_F

Mengden bevegelse P_enten før kollisjon er det samme som etter kollisjon. Dette blir oppfylt for enhver type kollisjon, både elastisk og uelastisk.

Nå må du vurdere følgende: Under en kollisjon opplever gjenstandene en viss deformasjon. Når sammenstøtet er elastisk, gjenvinner objekter raskt sin opprinnelige form.

[TOC]

Kinetisk energibesparing

Normalt under et sjokk blir en del av gjenstandens energi brukt på varme, deformasjon, lyd og noen ganger til og med i å produsere lys. Så den kinetiske energien i systemet etter kollisjonen er mindre enn den opprinnelige kinetiske energien.

Når kinetisk energi k, bevares den da:

K_enten = K_F

Noe som betyr at kreftene som virker under kollisjon er konservative. Mens kollisjonen varer den kinetiske energien blir kort omgjort til potensiell energi og så er det en kinetisk energi igjen. De respektive kinetiske energiene varierer, men summen forblir konstant.

Perfekt elastiske kollisjoner er ikke hyppige, selv om biljardkuler er en ganske god tilnærming, så vel som kollisjoner som foregår mellom ideelle gassmolekyler.

Elastiske sjokk i en dimensjon

La oss undersøke en kollisjon av to partikler av dette i en enkelt dimensjon; Det vil si at partiklene som samhandler, sier, langs x -aksen. Anta at de har masser m₁ og m₂. De første hastighetene til hver er eller₁ og eller₂ henholdsvis. De endelige hastighetene er v₁ og v₂.

Vi kan klare oss uten vektornotasjonen, siden bevegelsen utføres langs x-aksen, men tegnene (-) og (+) indikerer betydningen av bevegelsen. Til venstre er negativ og til den positive høyre, etter stevne.

Kan tjene deg: Bravais nettverk: konsept, egenskaper, eksempler, øvelser

-Formler for elastiske kollisjoner

For bevegelsesmengden

m₁eller₁ + m₂eller₂ = m₁v₁ + m₂v₂

For kinetisk energi

½ m₁eller²₁ + ½ m₂eller²₂ = ½ m₁v²₁ +  ½ m₂v²₂

Hver gang de innledende massene og hastighetene er kjent, er det mulig å omgruppere ligningene for å finne de endelige hastighetene.

Problemet er at det i prinsippet er nødvendig. Idealet ville være å finne uttrykk som ikke inneholder dem.

Den første er å gjøre uten ½ faktor og omorganisere begge ligningene på en slik måte at et negativt tegn vises og massene kan være faktor:

m₁eller₁ - m₁v₁ = M₂v₂ - m₂eller₂

m₁eller²₁ - m₁v²₁  = +M₂v²₂ - m₂eller²₂

Blir uttrykt på denne måten:

m₁(eller₁ - v₁ ) = m₂(v₂ - eller₂)

m₁(eller²₁ - v²₁ ) = m₂ (v²₂ - eller²₂)

Forenkling for å eliminere firkanter fra hastigheter

Nå må du bruke det bemerkelsesverdige produktet, det øker forskjellen i den andre ligningen, som oppnår et uttrykk som ikke inneholder rutene, som opprinnelig ønsket:

m₁(eller₁ - v₁ ) = m₂(v₂ - eller₂)

m₁(eller₁ - v₁ ) (eller₁ + v₁ ) = m₂ (v₂ - eller₂) (v₂ + eller₂)

Neste trinn er å erstatte den første ligningen i den andre:

m₂(v₂ - eller₂) (eller₁ + v₁ ) = m₂ (v₂ - eller₂) (v₂ + eller₂)

Og når begrepet gjentas m₂(v₂ - eller₂) På begge sider av likhet blir dette begrepet kansellert og er slik:

(eller₁ + v₁) = (V₂ + eller₂)

Eller enda bedre:

eller₁ - eller₂= v₂ -  v₁

Endelige hastigheter v₁ og v₂ av partiklene

Nå er det to lineære ligninger som det er lettere å jobbe med. Vi vil plassere dem igjen under den andre:

m₁eller₁ + m₂eller₂ = m₁v₁ + m₂v₂

eller₁ - eller₂= v₂ -  v₁

Multiplisere den andre ligningen med m₁ Og legge til termin til termin gjenstår:

m₁eller₁ + m₂eller₂ = m₁v₁ + m₂v₂

m₁eller₁ - m₁eller₂= m₁v₂ - m₁ v₁

-

2 m₁eller₁ + (m₂ - m₁) eller₂ = (m₂ + m₁) v₂

Og det er allerede mulig å fjerne v₂. For eksempel:

En lignende behandling kan gjøres for å finne en ligning for v₁. Leseren er igjen som en øvelse for å demonstrere at:

Spesielle tilfeller i elastiske kollisjoner

Nå som ligninger er tilgjengelige for de endelige hastighetene til begge partiklene, er det på tide å analysere noen spesielle situasjoner.

To identiske masser

Deretter m₁ = m₂ = m og:

v₁ = u₂

v₂ = u₁

Partikler utveksler ganske enkelt hastighetene etter kollisjon.

To identiske masser, hvorav en opprinnelig var i ro

En gang til  m₁ = m₂ = m og antar det eller₁ = 0:

v₁ = u₂

v₂ = 0

Etter krasjet får partikkelen som var i ro samme hastighet på partikkelen som hadde beveget seg, og den stopper igjen.

Kan tjene deg: hydraulisk trykk

To forskjellige masser, en av dem opprinnelig i ro

I dette tilfellet, antar eller₁ = 0, Men massene er forskjellige:

Hva om m₁ er mye større enn m₂?

Det hender at m₁ Hold i ro og m₂ Den returneres med samme hastighet som den påvirket.

Huygens-Newton restitusjonskoeffisient eller regel

Tidligere ble følgende forhold mellom hastighetene for to objekter i elastisk kollisjon trukket ut: eller₁ - eller₂ = v₂ -  v₁. Disse forskjellene er de relative hastighetene før og etter kollisjonen. Generelt for en kollisjon blir det oppfylt at:

eller₁ - eller₂ = -(v₁ -  v₂)

Det relative hastighetskonseptet blir bedre verdsatt hvis leseren forestiller seg at det er på en av partiklene og fra denne posisjonen observerer hastigheten som den andre partikkelen beveger seg. Den forrige ligningen blir skrevet om slik:

Hvis kinetisk energi ikke er bevart, vil den indikerte kvotienten være mindre enn 1. La oss ringe og til verdien av nevnte dimensjonsløs kvotient:

O vel:

Verdien av og er mellom 0 og 1 og kalles Restitusjonskoeffisient. Når sammenstøtet er elastisk, E = 1. Når det er helt uelastisk, E = 0, mens hvis den har noen annen mellomverdi, har noen kinetisk energi spredt seg i andre typer energi.

Løste øvelser

-Trening løst 1

En biljardkule beveger seg til venstre på 30 cm/s, og kolliderer foran med en annen identisk ball som beveger seg til høyre til 20 cm/s. De to ballene har samme deig og krasjet er perfekt elastisk. Finn hastigheten på hver ball etter påvirkning.

Løsning

eller₁ = -30 cm/s

eller₂ = +20 cm/s

Dette er spesialsaken som to identiske masser kolliderer i en elastisk dimensjon, derfor utveksles hastighetene.

v₁ = +20 cm/s

v₂ = -30 cm/s

-Trening løst 2

Restitusjonskoeffisienten til en ball som spretter på bakken er lik 0,82. Hvis du faller fra hvile, vil hvilken brøkdel av den opprinnelige høyden din nå ballen etter å ha sprett en gang? Og etter 3 returer?

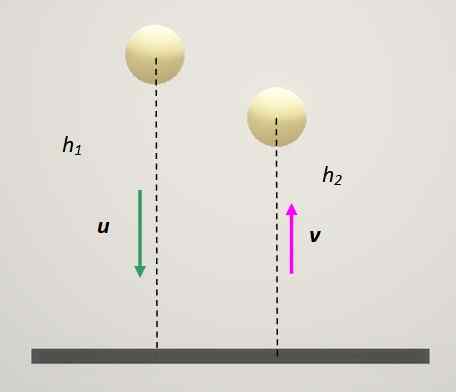En ball spretter mot en fast overflate og mister høyden med hvert rebound. Kilde: Selvlaget.

Løsning

Jorda kan være objekt 1 i restitusjonskoeffisientligningen. Og det er alltid i ro, slik at:

Den negative retningen er valgt ned og det positive. Hastigheten til et objekt som fritt frigjøres fra en viss høyde h_enten er:

Tegnet (-) indikerer at ballen synker ned:

Det kan tjene deg: torricelli eksperiment: atmosfærisk trykkmål, betydning

 

Med denne hastigheten som spretter:

 

+ -Tegnet indikerer at det er en stigende hastighet. Og ifølge den når ballen en maksimal høyde på:

 

Nå kommer han tilbake til bakken igjen med hastighet i samme størrelse, men det motsatte tegnet:

Og spretter med:

Dette når en maksimal høyde på:

Nå bakken igjen med:

Påfølgende returer

Hver gang ballen spretter og stiger opp, må du multiplisere hastigheten igjen med 0.82:

Og når en maksimal høyde bestemt av kvadratet med nevnte hastighet:

På dette tidspunktet h₃ er omtrent 30% av h_enten. Hva som ville være høyden på 6. returer uten å måtte foreta beregninger så detaljerte som de forrige?

jeg ville vært h₆ = 0.82¹² h_enten = 0.092H_enten eller bare 9% av h_enten.

-Trening løst 3

En 300 g blokk beveger seg nord til 50 cm/s og sammenstøt mot en 200 g blokk som er rettet sør 100 cm/s. Anta at sammenstøtet er perfekt elastisk. Finn hastighetene etter påvirkning.

Data

m₁ = 300 g; eller₁ = + 50 cm/s

m₂ = 200 g; eller₂ = -100 cm/s

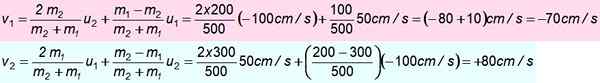
-Trening løst 4

En masse m frigjøres₁ = 4 kg fra punktet som er angitt på banen uten friksjon, til det kolliderer med m₂ = 10 kg i ro. Til hva en høyde er m₁ Etter kollisjonen?

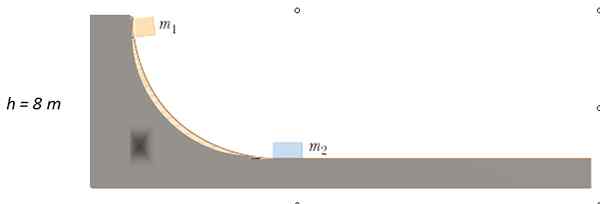
Løsning

Siden det ikke er noen friksjon, bevares mekanisk energi for å finne hastigheten eller₁ med hva m₁ påvirkninger  m_2. Opprinnelig er kinetisk energi 0, siden m₁ En del av resten. Når du beveger deg på den horisontale overflaten, har den ingen høyde, så den potensielle energien er 0.

Mgh = ½ mu₁ ²

 

eller₂ = 0

Nå hastigheten på m₁ Etter kollisjonen:

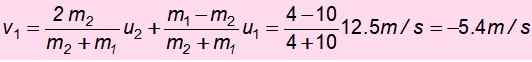
Det negative tegnet betyr at det er returnert. Med denne hastigheten stiger opp og mekanisk energi bevares igjen for å finne H ', Høyden som den klarer å stige opp etter krasjet:

½ mv₁² = mgh '

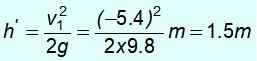
Merk at du ikke kommer tilbake til utgangspunktet på 8 m høyde. Den har ikke nok energi fordi den ga en del av sin kinetiske energi massen m_1.

Referanser

1. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Fundamentals of Physics. Pearson. 135-155.
3. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9^na Cengage Learning. 172 -182
4. Tipler, s. (2006) Fysikk for vitenskap og teknologi. 5. utg. Volum 1. Redaksjon tilbake. 217-238
5. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. MacGraw Hill. 185 -195