Brayton syklusprosess, effektivitet, applikasjoner, øvelser

Han Brayton Cycle Det er en termodynamisk syklus som består av fire prosesser og gjelder en komprimerbar termodynamisk væske som en gass. Hans første omtale stammer fra slutten av 1700 -tallet, selv om han tilbrakte litt tid før han ble oppvokst av James Joule. Det er derfor det også er kjent som Joule -syklusen.

Den består av følgende trinn, som enkelt er illustrert i trykkdiagrammet - volumet i figur 1: adiabatisk kompresjon (ingen varme byttes), isobarisk ekspansjon (oppstår ved konstant trykk), adiabatisk ekspansjon (ingen varme byttes) og isobar kompresjon (oppstår ved konstant trykk).

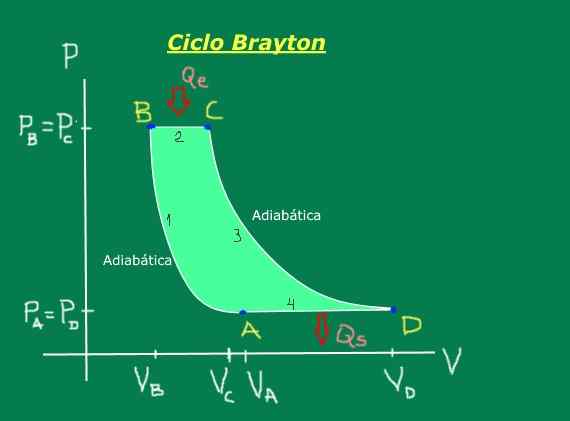Figur 1. Brayton Cycle. Kilde: Selvlaget.

[TOC]

Prosess og beskrivelse

Brayton-syklusen er den ideelle termodynamiske syklusen som brukes best for å forklare den termodynamiske funksjonen til gassturbiner og blander luftdrivstoff, brukt til generering av elektrisitet og i luftfartsmotorer.

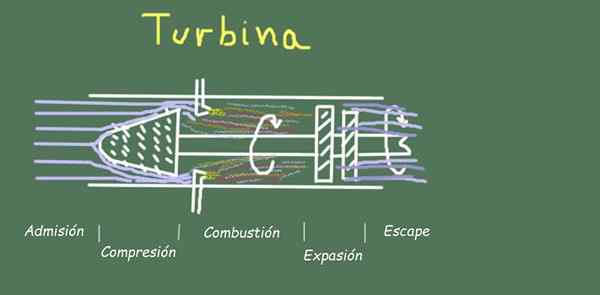Figur 2. Turbinordning og strømningsstadier. Kilde: Selvlaget.

For eksempel i drift av en turbin er det flere stadier i strømmen av operasjonsgass, som vi vil se nedenfor.

Adgang

Det består av luftinnløpet ved temperatur og miljøtrykk på grunn av åpningen av turbinen.

Komprimering

Luften komprimeres ved å spinne paletter mot andre som er festet i delen av turbinkompressoren. Denne komprimeringen er så rask at det praktisk talt ikke er noen varmeutveksling, så den modelleres gjennom Brayton Cycle AB -prosessen. Luften ved avkjørselen til kompressoren har hevet trykket og temperaturen.

Forbrenning

Luften er blandet med propankass eller pulverisert drivstoff som introduseres av injektorene i forbrenningskammeret. Blandingen produserer en kjemisk forbrenningsreaksjon.

Denne reaksjonen er den som gir varmen som øker temperaturen og kinetiske energien til gasspartiklene som utvides i forbrenningskammeret ved konstant trykk. I Brayton -syklusen er dette trinnet modellert med BC -prosessen som oppstår ved konstant trykk.

Ekspansjon

I delen av selve turbinen fortsetter luften å utvide seg mot turbinpalettene som får den til å rotere og produsere mekanisk arbeid. I dette trinnet senker luften temperaturen, men uten å utveksle varme praktisk med miljøet.

I Brayton -syklusen er dette trinnet simulert som en adiabatisk ekspansjonsprosess -CD. En del av turbinens arbeid overføres til kompressoren, og den andre brukes til å flytte en generator eller en propell.

Eksos

Den utgående luften er under konstant trykk lik miljø og gir varme til den enorme massen av ytre luft, så på kort tid tar det den samme innløpslufttemperaturen. I Brayton -syklusen er dette trinnet simulert med den konstante trykkprosessen, og lukker den termodynamiske syklusen.

Effektivitet basert på temperatur, varme og trykk

Vi foreslår å beregne effektiviteten til Brayton -syklusen, som vi starter fra definisjonen av det samme.

I en termisk maskin er effektiviteten definert som nettarbeidet utført av maskinen delt av varmeenergien som er gitt.

Det kan tjene deg: lett refleksjon

Det første prinsippet om termodynamikk slår fast at nettvarmen bidro til en gass i en termodynamisk prosess er lik variasjonen av den indre energien til gass pluss arbeidet som er gjort av det samme.

Men i en komplett syklus er variasjonen av indre energi ugyldig, så det har at nettvarmen som er bidratt i syklusen er lik nettarbeidet som er utført.

Innkommende varme, utgående varme og effektivitet

Det forrige uttrykket lar oss skrive effektivitet basert på absorbert eller innkommende varme (positvo) og varmen tildelt eller utgående QS (negativ).

Varme og trykk i Brayton -syklusen

I Brayton -syklusen kommer varmen inn i BC isobarisk prosess og kommer ut i den isobariske prosessen.

Forutsatt at ikke med konstant trykk som leveres med sensitiv varme som i BC -prosessen, øker temperaturen fra TB til TC i henhold til følgende forhold:

Hvor cp Det er varmekapasiteten med konstant trykk.

Den utgående varmen QS Det kan beregnes på samme måte ved følgende forhold som gjelder prosessen ved konstant trykk gir:

Å erstatte disse uttrykkene i uttrykket som gir oss effektivitet basert på innkommende varme og avtroppende varme, noe som gjør de relevante forenklingene følgende forhold for effektivitet oppnås:

Noe som resulterer i at effektiviteten er uavhengig av luftmassen som passerer gjennom turbinen.

Forenklet resultat

Det er mulig å forenkle det forrige resultatet hvis vi tar hensyn til det PA = PD og? PB = PC Siden AD- og BC -prosesser er Isobárica, det vil si med samme trykk.

I tillegg, ettersom AB- og CD -prosessene er adiabatiske, er Poissons forhold for begge prosesser oppfylt:

Hvor Gamma representerer den adiabatiske kvotienten, det vil si kvotienten mellom varmekapasiteten ved konstant trykk og varmekapasiteten ved konstant volum.

Ved å bruke disse forholdene og forholdet mellom tilstandsligningen til en ideell gass kan vi oppnå et alternativt uttrykk for Poissons forhold:

Som vi vet det PA = PD og? PB = PC erstatning og dele medlem til medlemmet, oppnås følgende forhold mellom temperaturer:

Hvis hvert medlem av den forrige ligningen trekkes fra enheten, blir forskjellen løst og vilkårene er faste, kan det påvises at:

Slik at effektiviteten kan skrives som en funksjon av lufttemperatur ved innløpet og lufttemperaturen ved slutten av komprimeringsprosessen AB.

Ytelse avhengig av trykkforholdet

Uttrykket oppnådd for effektiviteten av Brayton -syklusen basert på temperaturer kan skrives om for å formuleres basert på trykkforholdet ved kompressorens utgang og inngang.

Dette oppnås hvis Poissons forhold mellom punkt A og B er kjent avhengig av trykk og temperatur, og oppnår at effektiviteten til syklusen er uttrykt som følger:

Det kan tjene deg: Relativt trykk: formel, hvordan det beregnes, eksempler, trening

Å være kvotienten mellom PB og PA.

Et typisk trykkforhold er 8. I dette tilfellet har Brayton -syklusen en teoretisk ytelse på 45%.

applikasjoner

Brayton -syklusen som modell gjelder gassturbiner som brukes i termoelektriske anlegg for å flytte generatorene som produserer strøm.

Det er også en teoretisk modell som passer godt til driften av turboheriske motorer som brukes i fly, men det er ikke aktuelt i det hele tatt i fly Turboreactors.

Når det er interessert.

Figur 3. Turbofan motor mer effektiv enn turboreaktor. Kilde: Pixabay

I fly Turboreaktorer er det derimot ikke interessert.

Tvert imot, det er interessert.

Løste øvelser

-Oppgave 1

En gassturbin som brukes i termoelektriske planter har et trykk ved 800 kPa kompressoruttak. Temperaturen på den innkommende gassen er miljøet og er 25 Celsius, og trykket er 100 kPa.

I forbrenningskammeret stiger temperaturen til 1027 Celsius for å komme inn i turbinen.

Bestem effektiviteten av syklusen, temperaturen på gassen ut av kompressoren og gasstemperaturen ved turbinuttaket.

Løsning

Når vi har gasstrykket ved kompressoren, og vi vet at inngangstrykket er atmosfæretrykk, så det er mulig å oppnå trykkforholdet:

R = Pb / Pa = 800 kPa / 100 kPa = 8

Som gassen som turbinen opererer med er en blanding av propan luft og gass, blir den adiabatiske koeffisienten for en ideell diatomisk gass deretter påført, det vil si en gamma på 1,4.

Effektiviteten vil da bli beregnet slik:

Der vi har brukt forholdet som gir effektiviteten til Brayton -syklusen avhengig av trykkforholdet i kompressoren.

Temperaturberegning

For å bestemme temperaturen ved avkjørselen til kompressoren, eller hva som er den samme temperaturen som gassen kommer inn i forbrenningskammeret, bruker vi forholdsforholdet med kompressorinngangen og avkjørsler temperaturer.

Hvis vi fjerner TB -temperaturen fra det uttrykket, oppnår vi:

Med andre ord, forfølgelsestemperaturen er 804.12 Celsius.

Som utøvelse av øvelsen må vi etter forbrenning temperaturen stiger til 1027 Celsius, for å komme inn i turbinen. En del av den termiske energien til gassen brukes til å bevege turbinen, så temperaturen ved utgangen av den må være lavere.

Kan tjene deg: Applikasjoner av energi, kraft, styrke, arbeidskonsepter

For å beregne temperaturen ved turbinutgangen vil vi bruke et forhold mellom temperaturen tidligere:

Derfra fjerner vi TD for å oppnå temperaturen ved turbinuttaket. Etter utførelse av beregningene er den oppnådde temperaturen:

TD = 143,05 Celsius.

-Oppgave 2

En gassturbin følger Brayton -syklusen. Presset mellom kompressorens avgang og inngang er 12.

Anta omgivelsestemperaturen på 300 K. Som tilleggsdata er det kjent at gasstemperaturen etter forbrenning (før inngangen til turbinen) er 1000K.

Bestem temperaturen ved utgangen fra kompressoren, og temperaturen ved turbinuttaket. Bestem også hvor mange kilo gass som sirkulerer gjennom turbinen i hvert sekund, vel vitende om at kraften i den er 30 kW.

Anta den spesifikke gassvarmen som konstant og ta verdien av den ved romtemperatur: CP = 1 0035 j / (kg k).

Anta også at kompresjonseffektiviteten i kompressoren og dekompresjonen i turbinen er 100%, noe som er en idealisering fordi tap i praksis alltid oppstår.

Løsning

For å bestemme temperaturen ved utgangen av kompressoren, kjent temperaturen ved inngangen, må vi huske at det er en adiabatisk komprimering, slik at Poissons forhold for AB -prosessen kan brukes.

På denne måten oppnår vi at TB -temperaturen ved kompressoren er gitt av:

På samme måte er dekompresjon av gassene som krysser turbinen, en adiabatisk prosess som vil samsvare med Brayton -syklusprosessen. Derfor kan vi bruke Poissons forhold for å oppnå turbinutløpstemperaturen.

For enhver termodynamisk syklus vil nettoarbeid alltid være lik nettvarmen som er utvekslet i syklusen.

I det forrige forholdet som er den innkommende (positive) varmen og QS den utgående (negative) varmen. I Brayton -syklusen forekommer disse utvekslingene BC- og DA -prosessene, begge Isobáricas.

Nettoarbeid per driftssyklus kan da uttrykkes avhengig av massen av gass som sirkulerte i den syklusen og temperaturen.

I dette uttrykket m Det er massen av gass som sirkulerte gjennom turbinen i en operasjonssyklus og CP Den spesifikke varmen.

Hvis vi tar derivatet med hensyn til tidspunktet for det forrige uttrykket, oppnår vi netto medium kraft basert på massestrømmen.

Lysning m poeng, og erstatte temperaturen, kraft og varmekapasitet for gass oppnår en massestrøm på 1578,4 kg/s.

Referanser

1. Alfaro, J. Termodynamiske sykluser. Gjenopprettet fra: fis.Puc.Cl.
2. Fernández J.F. Brayton Cycle. Gassturbin. ELLER.T.N. (Mendoza). Gjenopprettet fra: Edutecne.Utn.Edu.ar.
3. Sevilla University. Fysikkavdeling. Brayton Cycle. Gjenopprettet fra: Laplace.oss.er.
4. National Experimental University of the Táchira. Transportfenomener. Gassens kraftsykluser. Gjenopprettet fra: UNET.Edu.gå.
5. Wikipedia. Brayton Cycle. Gjenopprettet fra: wikiwand.com
6. Wikipedia. Gassturbin. Gjenopprettet fra: wikiwand.com.