Blandet elektrisk krets

Vi forklarer hva som er en blandet krets, dens egenskaper, deler, symboler og gir flere eksempler

Hva er en blandet krets?

Han Blandet elektrisk krets Det er en som inneholder elementer koblet både i serie og parallelt, slik at når man lukker kretsen, er det etablert forskjellige spenninger og strømmer i hver av dem.

Kretsene er designet med et bredt utvalg av mål, og deres elementer tilhører to kategorier: eiendeler og forpliktelser.

De aktive elementene i kretsen er generatorer eller spenning eller strømkilder, direkte eller vekslende. På den annen side er de passive elementene motstanden, kondensatorene eller kondensatorene og spolene. Både en og andre innrømmer forbindelser i serie og parallelle, samt kombinasjoner av disse.

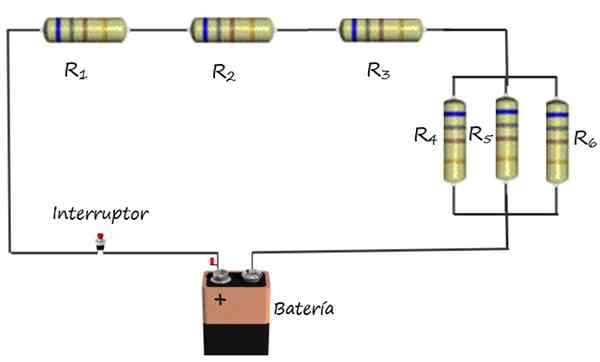
Den øverste figuren viser som et eksempel en blandet assosiasjon av elektriske motstander med et batteri og en bryter. Motstand r₁, R₂ og r₃ De er assosiert i serie, mens R -motstander₄, R₅ og r₆ De er koblet parallelt.

Andre mulige forbindelser, forskjellige fra serie-parallelle assosiasjoner, er delta (eller trekant) og stjerne, ofte brukt i elektriske maskiner matet med vekselstrøm.

Kjennetegn på en blandet krets

Generelt observeres følgende i en blandet krets:

• Kretsfôr kan være gjennom en direkte generator (batteri) eller veksle.
• Det anses at kablene eller ledningene som forener de forskjellige elementene ikke tilbyr gjeldende motstand.
• Både spenning og strøm kan være konstant eller variabel i tid. Kapital bokstaver brukes til å betegne konstante verdier, og små bokstaver når de var variabel.
• I rent resistive blandede kretsløp er strømmen gjennom seriemotstander den samme, mens i parallelle motstander generelt er den annerledes. For å beregne strømmen og spenningen gjennom hver motstand, reduseres vanligvis kretsen til en unik motstand, kalt ekvivalent motstand eller r_Eq .

Det kan tjene deg: Vektor subtraksjon: grafisk metode, eksempler, øvelser

Seriemotstander

Motstand parallelt

• Hvis kretsen består av N -kondensatorer, når den ekvivalente kapasitansen C er assosiert i serie_Eq resultat:

Seriekondensatorer

Parallelle kondensatorer

• Spolene eller induktorene følger de samme assosiasjonsreglene som motstand. Når du vil redusere en seriespoleforening for å oppnå den ekvivalente induktansen L_Eq, Følgende formler brukes:

Serielle induktorer

Induktorer parallelt

• For å løse blandede kretsløp med motstander, brukes OHM -loven og Kirchoff -lovene. I enkle resistive kretsløp er Ohms lov nok, men for mer komplekse nettverk er det nødvendig til stede.

Forholdet mellom spenning og strøm

Avhengig av kretselementet er det en sammenheng mellom spenningen eller spenningen gjennom elementet med intensiteten til strømmen som passerer gjennom den:

Motstand r

Ohms lov brukes:

v_R(t) = r ∙ i_R(T)

Kondensator c

Induktans l

Deler av en blandet krets

I en elektrisk krets skilles følgende deler:

Knute

Union Point mellom to eller flere ledende ledninger som forbinder noen aktive eller forpliktelser i kretsen.

Gren

Elementer, enten det er aktive eller forpliktelser, som er mellom to knuter på rad.

Mesh

Lukket del av kretsen reiste uten å passere to ganger gjennom samme punkt. Det kan ha eller ikke ha en spenning eller strømgenerator.

Kirchoff -lover eller regler

Kirchoff -regler gjelder både om strømmer og spenninger er konstante eller om de er avhengige av tid. Selv om de vanligvis kalles lover, er de faktisk regler for å anvende bevaringsprinsipper på elektriske kretsløp.

Kan tjene deg: Solid State Physics: Egenskaper, struktur, eksempler

Første regel

Den fastslår prinsippet om bevaring av belastningen, og påpeker at summen av dagens intensiteter som kommer inn i en knute, tilsvarer summen av intensitetene som kommer ut av den:

∑ i_inngang = ∑ i_exit

Andre regel

Ved denne anledningen er prinsippet om energibesparing etablert, når det sier at den algebraiske summen av spenninger i en lukket del av kretsen (nettet) er null.

∑ VI = 0

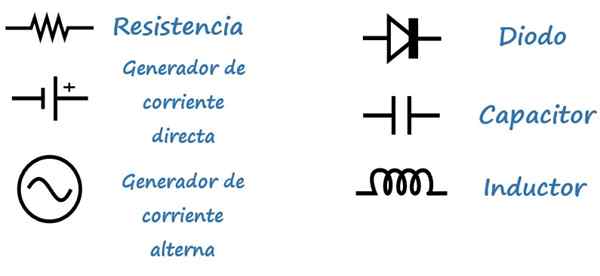
Symboler

For å lette analysen av kretsene, brukes følgende symboler:

Eksempler på blandede krets

Eksempel 1

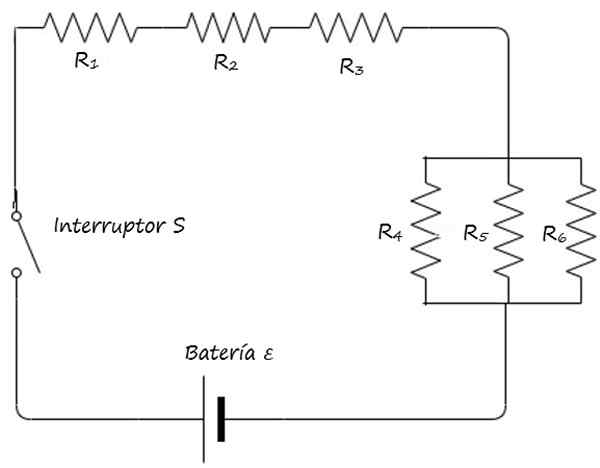
Tegn den blandede kretsen til startfiguren kompakt, ved å bruke symbolene beskrevet ovenfor.

Svar

Eksempel 2

I kretsen i eksempel 1 har du følgende verdier for motstander og batteri:

R₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω, r₄ = 24 Ω, r₅ = 48 Ω; R₆ = 48 Ω; ε = 100 V

For kretsen som vises, anses batteriet som ideelt, det vil si at det ikke har noen intern motstand. Vanligvis har ekte batterier en liten indre motstand som er tegnet i serie med batteriet og blir behandlet på samme måte som de andre motstandene i kretsen.

Beregn følgende:

• a) Kretsens tilsvarende motstand.
• b) Verdien på strømmen som kommer ut av batteriet.
• c) Spenningene og strømningene i hver av motstandene.

Svar til

Den første gruppen av motstand: r₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω er koblet i serie, derfor er den ekvivalente motstanden r₁₂₃:

R₁₂₃ = R₁ + R₂ + R₃ = 50 Ω + 100 Ω + 75 Ω = 225 Ω

Det kan tjene deg: Tredje lov om termodynamikk: Formler, ligninger, eksempler

Når det gjelder R -motstandsgruppen₄ = 24 Ω, r₅ = 48 Ω; R₆ = 48 Ω, er koblet parallelt og den tilsvarende formelen må brukes:

 Det gjensidige eller omvendte av det forrige resultatet er den tilsvarende motstanden for gruppen:

R₄₅₆ = 12 Ω

Den forenklede kretsen som er oppnådd vises i følgende graf, bestående av to seriemotstander med batteriet eller batteriet. Disse to motstandene legges til for å finne den tilsvarende motstanden til den opprinnelige R -kretsen_Eq:

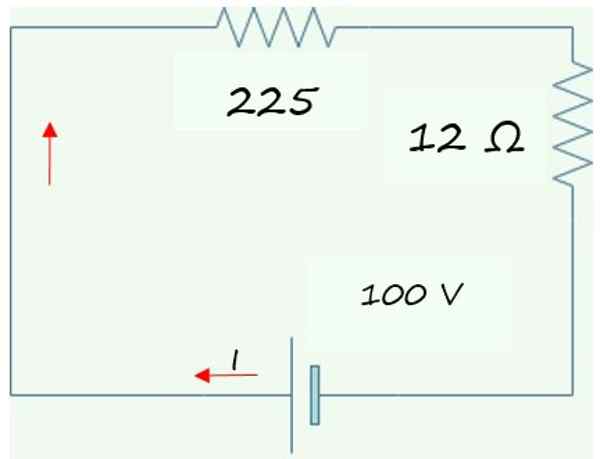
R_Eq= 225 Ω + 12 Ω = 237 Ω

Svar b

Strømmen som etterlater batteriet (etter stevne er alltid tegnet av den positive polen) beregnes med den forenklede kretsen, som består av den ekvivalente motstanden r_Eq i serie med batteriet, som Ohms lov brukes til:

ε = i · r

I = ε / r = 100 V / 237 Ω = 0.422 a

Svar c

Spenninger og strømmer i hver av SA -motstandene beregnet etter Ohms lov. Det første som blir observert er at strømmen som kommer ut av batteriet krysser motstandene R totalt₁ , R₂ og r₃ Og i stedet er det delt ved å krysse r₄ , R₅ og r₆.

Spenningene v₁, V₂ og v₃ er:

V₁  = 0.422 A × 50 Ω = 21.1 v
V₂  = 0.422 A × 100 Ω = 42.2 v
V₃  = 0.422 A × 75 Ω = 31.7 v

For sin del, Voljes v₄, V₅ og v₆ De har samme verdi, siden motstandene er parallelle:

V₄ = V₅ = V₆ = 0.422 A × 12 Ω = 5.06 v

Og de respektive strømningene er:

Yo₄ = 5.06 V / 24 Ω = 0.211 a

Yo₅ = Jeg₆ = 5.06 V / 48 Ω = 0.105 a

Merk at ved å legge til i₄, Yo₅ og jeg₆ Den totale strømmen som kommer ut av batteriet oppnås igjen.