Klassifisering av reelle tall

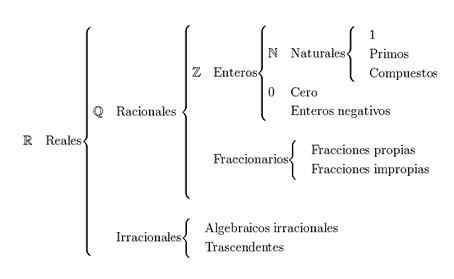
Hoved Klassifisering av reelle tall Det er delt inn i naturlige tall, hele tall, rasjonelle tall og irrasjonelle tall. De reelle tallene er representert med bokstaven r.

Reelle tall refererer til kombinasjonen av rasjonelle og irrasjonelle tallgrupper. For å danne disse gruppene er det nødvendig med naturlige tall og hele tall.

Det er mange måter de forskjellige reelle tallene kan bygges eller beskrives, varierende fra enklere former til mer komplekse former, avhengig av det matematiske arbeidet du vil utføre.

Hvordan klassifiseres reelle tall?

- Naturlige tall

Naturlige tall er representert med bokstav (n) og er de som brukes til å telle (0,1,2,3,4 ...). For eksempel "det er femten Rosas i hagen ”,“ Befolkningen i Mexico er fra 126 millioner av mennesker "eller" summen av to og to er fire"". Det skal bemerkes at noen klassifiseringer inkluderer 0 som et naturlig tall og andre ikke. 

To barn som lager en sum av to naturlige tall.

Naturlige tall inkluderer ikke de som har en desimaldel. Derfor er "befolkningen i Mexico fra 126.2 millioner av mennesker "eller" gjør en temperatur på 24.5 Celsius grader ”naturlige tall kunne ikke vurderes.

På vanlig språk, for eksempel barneskoler, kan naturlige tall kalles regnskapsnummer for å ekskludere negative heltall og null.

Naturlige tall er basene som mange andre sett med tall kan bygges med forlengelse: hele tall, rasjonelle tall, reelle tall og komplekse tall, blant andre.

Egenskapene til naturlige tall, for eksempel delbarhet og distribusjon av primærtall, studeres i tallteori. Problemene relatert til telling og bestilling, for eksempel oppregninger og partisjon, studeres i kombinatoriske.

De har flere egenskaper, for eksempel: sum, multiplikasjon, subtraksjon, divisjon, etc.

Kan tjene deg: samtidsvitenskap

Ordinære og kardinalnumre

Naturlige tall kan være ordinær eller kardinal.

Kardinalnumre vil være de som brukes som naturlige tall, som nevnt ovenfor i eksemplene. "Ha to informasjonskapsler "," Jeg er far til tre barn ”,“ Boksen inkluderer to Gavekremer ". 

Ordinaler er de som uttrykker orden eller angir en stilling. I et løp er for eksempel rekkefølgen av løperne oppført av vinneren og avslutter den siste som kom til målstreken.

På denne måten vil det bli sagt at vinneren er den "første", den neste "sekundet", den neste "tredje" og så videre til sist. Disse tallene kan være representert med et brev i øvre høyre for å forenkle forfatterskapet (1., 2., 3., 4., etc.).

- Heltallstall

Hele tallene består av de naturlige tallene og deres motsetninger, det vil si de negative tallene (0, 1, -1, 2, -2, 50, -50 ...). Som naturlige tall inkluderer disse ikke de som har en desimal del.

Eksempel på hele tall ville være "gjennomsnittlig 30. plass i Tyskland", "Jeg bodde på 0 når jeg nådde slutten av måneden", "For å gå ned til kjelleren må du merke heisknappen" på heisen ".

I sin tur kan ikke hele tall skrives med en brøkkomponent. For eksempel tall som 8.58 eller √2 er ikke hele tall.

Hele tall er representert med bokstaven (z). Z er en underpail -gruppe av rasjonelle tall q, som igjen danner gruppen av reelle n -tall. Som naturlige tall er Z en uendelig regnskapsgruppe.

Heltall danner den minste gruppen og det minste settet med naturlige tall. I algebraiske tallteori kalles hele tall noen ganger irrasjonelle for å skille dem fra algebraiske heltall.

Det kan tjene deg: Forskningsprosjekt: Fester, hvordan det er utdypet og eksempel

- Rasjonelle tall

Settet med rasjonelle tall er representert med bokstav (Q) og inkluderer alle tallene som kan skrives som en brøkdel av hele tall.

Det vil si at dette settet inkluderer naturlige tall (4/1), hele tall (-4/1) og eksakte desimaltall (15,50 = 1550/100).

Distribusjonen av 1/6 ost er et rasjonelt tall.

Desimalutvidelsen av et rasjonelt tall ender alltid etter et begrenset antall sifre (f.eks. 15.50) eller når den samme endelige sifre sekvens begynner å bli gjentatt igjen og igjen (f.eks. 0.3456666666666666 ...). Derfor, innenfor settet med rasjonelle tall er tallene inkludert. rene aviser eller blandede aviser.

I tillegg representerer enhver gjentatt eller terminal desimal et rasjonelt tall. Disse uttalelsene stemmer ikke bare for base 10, men også for noe annet basenummer.

Et reelt tall som ikke er rasjonelt kalles irrasjonelt. Irrasjonelle tall inkluderer √2, π og e, for eksempel. Siden hele settet med rasjonelle tall er følelsesmessig, og at gruppen av reelle tall ikke er følbar, kan det sies at nesten alle reelle tall er irrasjonelle.

Rasjonelle tall kan formelt defineres som ekvivalensklasser av hele par (P, Q) slik at Q ≠ 0 eller det ekvivalente forholdet definert av (P1, Q1) (P2, Q2) bare hvis P1, Q2 = P2Q1.

De rasjonelle tallene, sammen med summen og multiplikasjonen, formfelt som utgjør hele tallene og er inneholdt av en hvilken som helst gren som inneholder hele.

- Irrasjonelle tall

Irrasjonelle tall er alle reelle tall som ikke er rasjonelle tall; Irrasjonelle tall kan ikke uttrykkes som brøk. De rasjonelle tallene er tallene som er sammensatt av brøkdeler av hele tall.

Som en konsekvens av sangerprøven som sier at alle reelle tall er ikke -nevnende og at de rasjonelle hvis de er tall, kan det konkluderes med at nesten alle reelle tall er irrasjonelle.

Kan tjene deg: bane og forskyvning

Når radiusen til to linjesegmenter er et irrasjonelt tall, kan det sies at disse linjesegmentene er umåtelige; noe som betyr at det ikke er en tilstrekkelig lengde slik at hver av dem kan være "mål" med et spesielt heltall av det samme.

Blant de irrasjonelle tallene er radius π for en sirkel sirkel til dens diameter, antall Euler (e), det gylne tallet (φ) og kvadratroten til to; Enda mer er alle kvadratiske røtter til naturlige tall irrasjonelle. Det eneste unntaket fra denne regelen er de perfekte rutene.

Det kan observeres at når irrasjonelle tall uttrykkes posisjonert i et tallsystem, (for eksempel desimaltall) ikke slutter eller gjentar.

Dette betyr at de ikke inneholder en sekvens av sifre, repetisjonen som en representasjonslinje blir gjort.

Forenkling av det irrasjonelle tallet pi.

For eksempel: Desimalrepresentasjonen av tallet π begynner med 3.14159265358979, men det er ingen begrenset antall sifre som kan representere π nøyaktig, og de kan heller ikke gjentas.

Beviset på at desimalutvidelsen av et rasjonelt antall må ende eller gjenta er forskjellig fra beviset på at en desimalforlengelse må være et rasjonelt tall; Selv om de er grunnleggende og noe lange, tar disse testene noe arbeid.

Vanligvis tar matematikere vanligvis ikke forestillingen om å "avslutte eller gjenta" for å definere konseptet med et rasjonelt tall.

Irrasjonelle tall kan også behandles via ikke -kontinuerlige fraksjoner.

Referanser

1. Klassifiserer reelle tall. Gjenopprettet fra chilimath.com.
2. Naturlig tall. Gjenopprettet fra Wikipedia.org.
3. Klassifisering av tall. Ditutor ble gjenopprettet.com.
4. Gjenopprettet fra Wikipedia.org.
5. Irrasjonelt tall. Gjenopprettet fra Wikipedia.org.