Konseptkoeffisientkonsept, formel, beregning, eksempel

Han Restitusjonskoeffisient Det er kvotienten mellom den relative hastighetshastigheten og den relative hastigheten på å nærme seg to kropper som kolliderer. Når kroppene er forent etter kollisjonen, er denne kvotienten ugyldig. Og enheten er verdt i tilfelle kollisjonen er perfekt elastisk.

Anta at to solide massesfærer M1 og masse M2 henholdsvis at de lider en kollisjon. Rett før kollisjon hadde sfærene hastigheter V1 og V2 Angående et visst treghetsreferansesystem. Rett etter kollisjon endres hastighetene deres til V1 ' og V2 '.

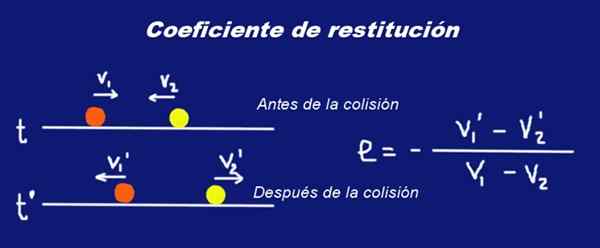Figur 1. Kollisjon av to sfærer av masser M1 og M2 og deres restitusjonskoeffisient og. Utarbeidet av Ricardo Pérez.

Brevet er plassert Fet skrift I hastigheter for å indikere at de er vektormengder.

Eksperimentene indikerer at hver kollisjon oppfyller følgende forhold:

V1 ' - V2 '= -og (V1 - V2)

Hvor og Det er et reelt tall mellom 0 og 1, kalt Restitusjonskoeffisient av kollisjonen. Det forrige uttrykket tolkes som følger: 

Den relative hastigheten til to partikler før kollisjonen er proporsjonal med den relative hastigheten til de to partiklene etter kollisjonen, er konstant av proporsjonalitet (-e), der e er koeffisienten for restitusjon av kollisjonen.

[TOC]

Hva er restitusjonskoeffisienten for?

Nytten av denne koeffisienten ligger i å kjenne grad av uelastisitet av en kollisjon. I tilfelle kollisjonen er perfekt elastisk, vil koeffisienten være 1, mens i en helt uelastisk kollisjon vil koeffisienten være verdt 0, siden i dette tilfellet den relative hastigheten etter kollisjonen er null.

Gjensidig, hvis restitusjonskoeffisienten for en kollisjon og hastighetene til partiklene er kjent før den, kan hastighetene forutsies etter slik kollisjon oppstår. 

Kan tjene deg: 13 eksempler på Newtons første lov i det virkelige liv

Momentumet

I kollisjoner, i tillegg til forholdet som er etablert av restitusjonskoeffisienten, er det et annet grunnleggende forhold, som er Momentum bevaring.

Momentumet p av en partikkel, eller mengden av bevegelse som den også kalles, er det produktet av massen M av partikkelen for sin hastighet V. Det vil si: momentumet p Det er en vektormengde.

I kollisjoner det lineære momentumet P Systemet er det samme rett før og like etter kollisjonen, fordi den utvendige kraften er foraktelig mot de korte, men intense kreftene med intern interaksjon under kollisjonen. Men bevaring av fart er ikke nok P av systemet for å løse det generelle problemet med kollisjonen.

I det tidligere nevnte tilfellet, det av de to M1- og M2 -kulene som kolliderer, er bevaring av det lineære momentum skrevet slik:

 M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .

Det er ingen måte å løse kollisjonsproblemet hvis restitusjonskoeffisienten ikke er kjent. Momentumbevaring, selv om det er nødvendig, er utilstrekkelig for å forutsi hastigheter etter kollisjon.

Når et problem sier at kroppene beveger seg sammen etter kollisjon, sier implisitt at restitusjonskoeffisienten er 0.

Figur 2. I biljardkulene er det kollisjoner av restitusjonskoeffisienten litt mindre enn 1. Kilde: Pixabay.

Energi- og restitusjonskoeffisient 

Den andre viktige fysiske mengden som er involvert i kollisjoner er energi. Under kollisjoner er det utveksling av kinetisk energi, potensiell energi og andre typer energi, for eksempel kalorienergi.

Før og etter kollisjon er den potensielle energien til interaksjon praktisk talt null, så energibalansen involverer den kinetiske energien til partiklene før og etter og en mengde Q kalt spredt energi.

Det kan tjene deg: Heisenberg Atomic Model

For de to M1- og M2 -masseskiftene som kolliderer energibalansen før og etter kollisjonen, er den skrevet slik:

½ m1 V1^2 + ½ m2 V2^2 = ½ m1 V1 '^2 + ½ m2 V2 '^2 + q

Når samhandlingskreftene under kollisjonen er rent konservative, skjer det det Total kinetisk energi Av partiklene som kolliderer er det bevart, det vil si at den er det samme før og etter kollisjonen (q = 0). Når dette skjer, sies det at kollisjon er perfekt elastisk.

I tilfeller av elastiske kollisjoner blir ikke energi forsvunnet. Og også restitusjonskoeffisienten samsvarer: E = 1. 

Tvert imot, i uelastiske kollisjoner at ≠ 0 og 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.

For at et kollisjonsproblem skal bli perfekt bestemt, er det nødvendig å kjenne restitusjonskoeffisienten, eller vekselvis mengden energi som ble spredt under kollisjonen.

Restitusjonskoeffisienten avhenger av arten og typen interaksjon mellom de to kroppene under kollisjonen.

På den annen side vil den relative hastigheten på kroppene før kollisjonen definere intensiteten til samspillet og derav dens innflytelse på restitusjonskoeffisienten. 

Hvordan beregnes restitusjonskoeffisienten?

For å illustrere hvordan restitusjonskoeffisienten for en kollisjon beregnes vil vi ta en enkel sak:

Anta at kollisjonen av to massesfærer M1 = 1 kg og M2 = 2 kg som går over en rett friksjon (som i figur 1).

Den første sfæren påvirker starthastigheten V1 = 1 m/s Omtrent det andre som opprinnelig er i ro, det vil si V2 = 0 m/s.

Det kan tjene deg: Første lov om termodynamikk: Formler, ligninger, eksempler

Etter kollisjonen beveger de seg slik: den første stopper (V1 '= 0 m/s) og den andre beveger seg til høyre med hastighet V2 '= 1/2 m/s.

For å beregne restitusjonskoeffisienten i denne kollisjonen bruker vi forholdet:

V1 ' - V2 ' = -og ( V1 - V2 ) 

0 m/s - 1/2 m/s = - e (1 m/s - 0 m/s) => - 1/2 = - e => e = 1/2 .

Eksempel

I den endimensjonale kollisjonen av de to sfærene i forrige seksjon, ble restitusjonskoeffisienten beregnet, noe som resulterte i E = ½ .

Ettersom E ≠ 1 er ikke kollisjonen elastisk, det vil si at den kinetiske energien i systemet ikke er bevart og det er en viss mengde spredt energi Q (for eksempel oppvarming av kulene på grunn av kollisjonen).

Bestem verdien av energien som er spredt i joules. Beregn også prosentvis brøkdel av spredt energi.

Løsning

Den første kinetiske energien til sfære 1 er: 

K1i = ½ m1 v1^2 = ½ 1 kg (1 m/s)^2 = ½ j

Mens den for Sphere 2 er null for å være i ro i ro.

Så den første kinetiske energien til systemet er ki = ½ j.

Etter kollisjonen beveger bare den andre sfæren med hastighet V2 '= ½ m/s, så den endelige kinetiske energien til systemet vil være:

Kf = ½ m2 v2 '^2 = ½ 2 kg (½ m/s)^2 = ¼ j

Det vil si at energien som er spredt i kollisjonen er:

Q = ki - kf = (½ j - ¼ j) = 1/4 j

Og brøkdelen av energi som er spredt i denne kollisjonen, beregnes som følger:

F = q / ki = ¼ / ½ = 0,5 Det vil si at 50% av systemenergien er blitt spredt på grunn av den uelastiske kollisjonen hvis restitusjonskoeffisient er 0,5.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Figueroa, d. 2005. Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
3. Knight, r. 2017. Fysikk for forskere og ingeniørfag: En strategitilnærming. Pearson.
4. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.
5. Wikipedia. Mengde bevegelse.Gjenopprettet fra: er.Wikipedia.org.