Kompresjonskonsept og formler, beregning, eksempler, øvelser

De komprimering eller kompresjonsinnsats Det er kraften per enhet med område hvis resultat er å skyve, stramme eller komprimere et objekt, og har en tendens til å forkorte det. Matematisk er:

E = f /a

Her OG Angi innsatsen, F størrelsen på styrken og TIL Området som enheten er i det internasjonale systemet hvis Newton/M² O Pascal (PA). Komprimeringsinnsats er en normal innsats, Fordi kraften som produserer den er vinkelrett på området den utøves.

Figur 1. Kolonnene i Akropolis i Athen er underlagt komprimering. Kilde: Pixabay.

Slik innsats kan komprimere objektet eller tvert imot, stramme det og strekke det, som påført. I tilfelle av komprimeringsinnsats gjelder krefter i motsatt retning for å utøve effekten av å stramme og forkorte objektet.

Når kreftene opphører, kommer mange materialer tilbake til sine opprinnelige dimensjoner. Denne egenskapen er kjent under navnet på elastisitet. Men mens det skjer, er den enhetlige elastiske deformasjonen som et materiale som er utsatt for en innsats:

Enhet deformasjon = (sluttstørrelse - startstørrelse)/startstørrelse

Deformasjon kan være lineær, overfladisk eller volum, selv om enhetsdeformasjon mangler enheter. Imidlertid er informasjonen den gir veldig viktig, siden den ikke er den samme å deform.

I et elastisk materiale er deformasjon og innsats proporsjonal, og i samsvar med Hooke's lov:

Innsats ∝ Unitary Deformation

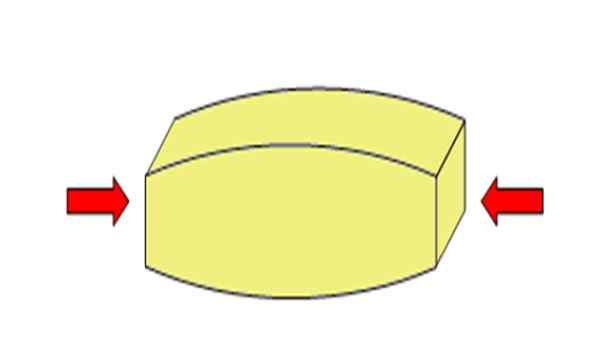Figur 2. Komprimeringsinnsatsen reduserer objektets lengde. Kilde: Wikimedia Commons. ADRE-ES [CC BY-SA 4.0 (https: // creativecommons.Org/lisenser/by-SA/4.0)].[TOC]

¿Hvordan beregne komprimering?

Kompresjonsinnsatsen gjør at partiklene i materialet kommer nærmere og mer, forkorter størrelsen. Avhengig av retningen innsatsen blir brukt, vil det være en forkortelse eller reduksjon i noen av dens dimensjoner.

Kan tjene deg: kvantemekanisk modell av atomet

La oss starte med å anta en tynn stang med original lengde L,  som normal størrelses innsats brukes OG. Hvis innsatsen er komprimering, opplever baren en reduksjon i lengden, betegnet av Δ. Hvis det er spenning, vil baren bli forlenget.

Naturligvis er materialet som elementet er laget avgjørende i sin evne til å støtte innsatsen.

Disse elastiske egenskapene til materialet er inkludert i den nevnte proporsjonalitetskonstanten. Er kalt Elastisitetsmodul enten Ung modul og det er betegnet som og. Hvert materiale har en elastisitetsmodul, som bestemmes eksperimentelt gjennom laboratorietester.

Med dette i bakhodet, innsatsen OG Det kommer til uttrykk på matematisk måte som dette:

Innsats ∝ Unitary Deformation

Til slutt, for å etablere denne tilstanden som en ligning, er det nødvendig med en konstant proporsjonalitet for å erstatte symbolet på proporsjonalitet ∝ og erstatte den med likhet, som dette:

Innsats = proporsjonalitet Konstant x enhetsdeformasjon        

E = y. (Δ /l)

Kvotienten (Δ /l) Det er den enhetlige deformasjonen, betegnet som ε og med Δ = Endelig lengde - startlengde. På denne måten er innsatsen OG Det forblir som:

E = y. ε

Siden enhetens deformasjon er dimensjonsløs, er enhetene til OG er de samme som av OG: N/m² eller PA på SI -systemet, pund/i² O PSI i det britiske systemet, så vel som andre kombinasjoner av styrke og område, for eksempel kg/cm².

Elastisitetsmodul med forskjellige materialer

Verdiene av og bestemmes eksperimentelt i laboratoriet, under kontrollerte forhold. Deretter er elastisitetsmodulen for materialer som er mye brukt i konstruksjon og også av bein:

Kan tjene deg: Vektorer i rommet: Hvordan graf, applikasjoner, øvelser

Tabell 1

Materiale	Elastisitetsmodul Y (PA) x 109
Stål	200
Jern	100
Messing	100
Bronse	90
Aluminium	70
Marmor	femti
Granitt	Fire fem
Betong	tjue
Bein	femten
Pinewood	10

Eksempler

Komprimeringsinnsats virker på forskjellige strukturer; Det samme som er underlagt virkning av krefter som vekten til hvert av elementene som utgjør dem, samt krefter fra ytre agenter: vind, snø, andre strukturer og mer.

Det er vanlig at de fleste strukturer skal utformes for å motstå innsats av alle slag uten å deformere. Derfor er det nødvendig å ta hensyn til komprimeringsinnsatsen for å forhindre at stykket eller objektet mister formen.

Også beinene i skjelettet er strukturer underlagt forskjellige anstrengelser. Selv om beinene er motstandsdyktige mot dem, stammer den elastiske grensen ved en tilfeldig.

Kolonner og søyler

Kolonnene og søylene i bygningene må lages for å motstå komprimering, ellers har de en tendens til å arge. Dette er kjent som Lateral fleksjon enten knekking.

Kolonnene (se figur 1) er elementer hvis lengde er mye høyere sammenlignet med området for tverrsnittet.

Et sylindrisk element er en kolonne når lengden er lik eller større enn ti ganger diameteren på tverrsnittet. Men hvis tverrsnittet ikke er konstant, vil dets mindre diameter bli tatt med det formål å klassifisere elementet som en kolonne.

Stoler og banker

Når folk tar plass i møbler som stoler og banker, eller legger til gjenstander på toppen, er bena utsatt for kompresjonsinnsats som har en tendens til å redusere høyden.

Figur 3. Når de sitter, utøver folk en komprimeringsinnsats på stolen, noe som har en tendens til å forkorte høyden. Kilde: Pixabay.

Vanligvis er møblene laget for å motstå vekten ganske godt og gå tilbake til deres naturlige tilstand når de er fjernet. Men hvis en stor vekt er lagt i skjøre stoler eller banker, gir bena til komprimering og brudd.

Kan tjene deg: elektriske ledere

Øvelser

- Oppgave 1

Du har en stang som opprinnelig måler 12 m i lengde, som den gjennomgår en komprimeringsinnsats slik at enhetsdeformasjonen er -0.0004. Hva er den nye stanglengden?

Løsning

Starter fra ligningen gitt ovenfor:

ε = (Δ /l) = - 0.0004

Ja L_F Det er den endelige lengden og L_enten den første lengden, siden Δ = l_F - L_enten  Du har:

(L_F - L_enten)/ L_enten = -0.0004

Derfor: L_F - L_enten = -0.0004 x 12 m = -0.0048 m. Og endelig:

L_F  = (12 - 0.0048) M = 11.9952 m.

- Oppgave 2

En solid stålstang, sylindrisk, måler 6 m lang og 8 cm i diameter. Hvis stangen blir utsatt for komprimering ved hjelp av en 90 belastning.000 kg, finn:

a) Størrelsen på kompresjonsinnsatsen i Megapascal (MPA)

b) Hvor mye reduserte lengden på stangen?

Løsning på

Først er område A i tverrsnittet av stangen, som avhenger av dens diameter d, noe som resulterer i:

A = π. D² / 4 = π. (0.08 m)² / 4 = 5.03 x 10^-3 m²

Styrken er umiddelbart gjennom F = m.G = 90.000 kg x 9.8 m/s²= 882.000 n.

Endelig beregnes den gjennomsnittlige innsatsen som følger:

E = f/ a = 882.000 N/ 5.03 x 10^-3 m² = 1.75 x 10⁸ PA = 175 MPa

Løsning b

Ligningen for innsatsen brukes nå, vel vitende om at materialet har elastisk respons:

E = y. (Δ /l)

Den unge modulen stål finnes i tabell 1:

Δ = e.L / y = 6 m x 1.75 x 10⁸ PA / 200 x 10 ⁹ PA = 5.25 x 10 ^-3 m = 5.25 mm.

Referanser

1. Øl, f. 2010. Materialmekanikk. 5. plass. Utgave. McGraw Hill.
2. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6^Tth  Ed. Prentice Hall.
3. Hibbeler, R.C. 2006. Materialmekanikk. 6. Utgave. Pearson Education.
4. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill
5. Wikipedia. Stress (mekanikk). Gjenopprettet fra: Wikipedia.org.