Finittlige settegenskaper, eksempler, øvelser løst

Det forstås av Endelig sett alt satt med et begrenset eller regnskapsmessig antall elementer. Eksempler på endelige sett er klinkekuler som er inneholdt i en pose, settet med hjem i et nabolag eller settet P dannet av de tjue (20) naturlige tallene:

P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13, 14, 16, 17, 18, 19, 20 

Settet med universets stjerner er sikkert enormt, men det er ikke sikkert kjent om det er begrenset eller uendelig. Imidlertid er settet med solsystemplaneter begrenset.

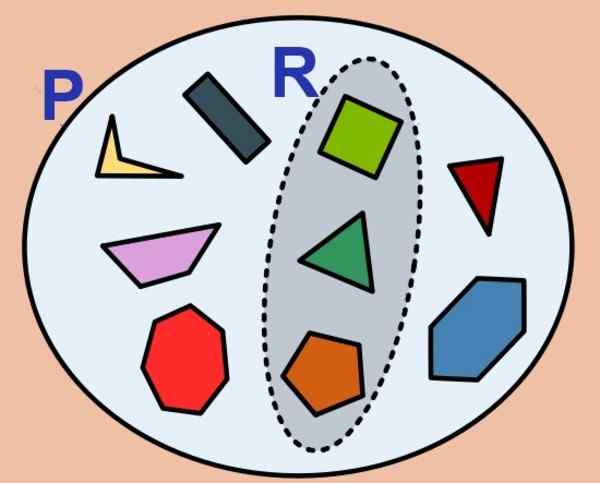
Figur 1. Settet med polygoner er begrenset og undergruppen av de vanlige også. (Wikimedia Commons)

Antall elementer i et begrenset sett kalles kardinaliteten og for settet P Det er betegnet slik: kort (P) enten #P. Det tomme settet har null kardinalitet og regnes som et begrenset sett.

[TOC]

Egenskaper

Blant egenskapene til endelige sett er følgende:

1- Foreningen av endelige sett resulterer i et nytt endelig sett.

2- Hvis to endelige sett er oppfanget, er det et nytt endelig sett.

3- En delmengde av et begrenset sett er begrenset og dets kardinalitet er mindre enn eller lik det for det originale settet.

4- Det tomme settet er et begrenset sett.

Eksempler

Det er mange eksempler på endelige sett. Blant noen eksempler er følgende:

Sett M av månedene, som kan utvides som følger:

M = Januar, februar, mars, april, mai, juni, juli, august, september, oktober, november, desember, er kardinaliteten til m 12.

Sett S av ukens dager: S = Mandag, tirsdag, onsdag, torsdag, fredag, lørdag, søndag. Kardinaliteten til S er 7.

Kan tjene deg: proporsjonalitetsrelasjoner: konsept, eksempler og øvelser

Sett Ñ Fra bokstavene i det spanske alfabetet er det et begrenset sett, dette settet i forlengelsen er skrevet slik:

Ñ = A, B, C, D, E, F, G, H, I, J, K, L, M, N, ñ, O, P, Q, R, S, T, U, V, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, X, Y, Z og dets Kardinalitet er 27.

Sett V Fra vokalene på spansk er det en delmengde av ñ -settet:

V ⊂ Ñ Derfor er det et begrenset sett.

Det endelige settet V Utvidet måte det er skrevet slik: V = a, e, i, o, u og dets kardinalitet er 5.

Sett kan uttrykkes ved forståelse. Sett F bestående av bokstavene i ordet "endelig" er et eksempel:

F = x / x er en bokstav i ordet "endelig"

Dette settet uttrykt mye vil være:

F = f, i, n, t, o hvis kardinalitet er 5 og derfor er det et begrenset sett.

Flere eksempler

Regnbuens farger er et annet endelig setteksempel, settet C av disse fargene er:

C = rød, oransje, gul, grønn, cyan, blå, fiolett og dens kardinalitet er 7.

Settet med faser F Fra månen er et annet endelig setteksempel:

F = New Moon, Growing Room, Full Moon, Waning Room Dette settet har kardinalitet 4.

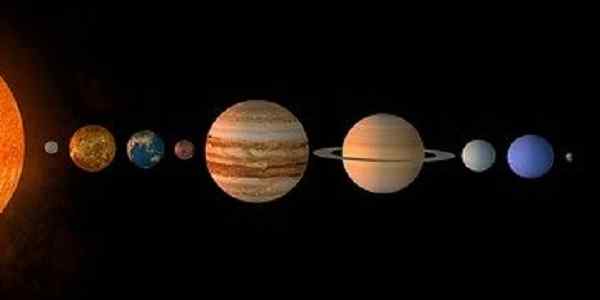Figur 2. Planetene til solsystemet danner et begrenset sett. (Pixabay)

Et annet endelig sett er det som er dannet av planetene i solsystemet:

P = Merkur, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto Cardinalitet 9.

Løste øvelser

Oppgave 1

Følgende sett er gitt a = x∊ r / x^3 = 27. Uttrykk det med ord og skriv det i forlengelse, angi kardinaliteten og si om det er begrenset eller ikke.

Kan tjene deg: ellipse

Løsning: Sett A er settet med reelle tall x slik at x hevet til kuben som et resultat 27.

Ligning x^3 = 27 har tre løsninger: som er x1 = 3, x2 = (-3/2 + 3√3/2 i) og x3 = (-3/2-3√3/2 i). Av de tre løsningene er bare x1 ekte, mens de to andre er komplekse tall.

Som definisjonen av sett A sier at X tilhører reelle tall, så er ikke løsninger i komplekse tall en del av settet til.

Det utvidede settet er:

A = 3, som er et begrenset sett med kardinalitet 1.

Oppgave 2

Skriv symbolsk (ved forståelse) og omfattende settet B for de virkelige tallene som er større enn 0 (null) og mindre eller lik enn 0 (null). Angi kardinaliteten din og om den er begrenset eller ikke.

Løsning: B = x∊ r / 0 < x <= 0

Sett B er tomt fordi et reelt tall x ikke kan være samtidig større og mindre enn null, så vel som 0 og også mindre enn 0.

B = og dens kardinalitet er 0. Det tomme settet er et begrenset sett.

Øvelse 3

S -settet med løsningene av en viss ligning er gitt. Settet av forståelse er skrevet slik:

S = x∊ r / (x -3) (x^2 - 9x + 20) = 0

Skriv dette settet mye, angi kardinaliteten din og angi om det er et begrenset sett eller ikke.

Løsning: For det første, ved å analysere uttrykket som beskriver settet S, oppnås det at det er et sett med reelle x -verdier som er løsninger på ligningen:

(x -3) (x^2 - 9x + 20) = 0 (*)

En løsning av denne ligningen er x = 3, som er et reelt tall og derfor tilhører S. Men det er flere løsninger som kan oppnås på jakt etter løsningene i den kvadratiske ligningen:

Kan tjene deg: Distribusjon F: Karakteristikker og øvelser løst

(x^2 - 9x + 20) = 0

Det forrige uttrykket kan faktor som følger:

(x - 4) (x - 5) = 0

Noe som fører oss til ytterligere to løsninger av den opprinnelige (*) ligningen som er x = 4 og x = 5. Kort sagt, ligning (*) har løsninger 3, 4 og 5.

S -settet uttrykt mye er slik:

S = 3, 4, 5, som har kardinalitet 3 og er derfor et begrenset sett.

Oppgave 4

Det er to sett a = 1, 5, 7, 9, 11 og b = x ∊ n / x er par ^ x x < 10 .

Skriv eksplisitt sett B og finn unionen med settet a. Finn også avskjæringen av disse to settene og konkludere.

Løsning: Sett B består av naturlige tall slik at de er jevn og også er lavere enn verdi 10, derfor er B i stor grad skrevet som følger:

B = 2, 4, 6, 8

Foreningen av sett A med sett B er:

A u b = 1, 2, 4, 5, 6, 7, 8, 9, 11

og avskjæringen av sett A med sett B er skrevet slik:

A ⋂ b = = Ø er det tomme settet. 

Det skal bemerkes at unionen og avskjæringen av disse to endelige settene fører til nye sett, som igjen også er endelig.

Referanser

1. Kilder, a. (2016). Grunnleggende matematikk. En introduksjon til beregning. Lulu.com.
2. GARO, m. (2014). Matematikk: Kvadratiske ligninger: Hvordan løse en kvadratisk ligning. Marilù Garo.
3. Haeussler, e. F., & Paul, r. S. (2003). Matematikk for administrasjon og økonomi. Pearson Education.
4. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematikk 1 september. Terskel.
5. Dyrebar, c. T. (2005). Matematikkurs 3o. Redaksjonell progreso.
6. Matematikk 10 (2018). "Eksempler på endelige sett". Hentet fra: Matematikk10.nett
7. Rock, n. M. (2006). Algebra jeg er lett! Så lett. Team Rock Press.
8. Sullivan, J. (2006). Algebra og trigonometri. Pearson Education.
9. Wikipedia. Endelig sett. Gjenopprettet fra: er.Wikipedia.com