Forskjell mellom en felles brøk og et desimaltall

Å identifisere Hva er forskjellen mellom en vanlig brøkdel og et desimaltall Det er nok å observere begge elementene: den ene representerer et rasjonelt tall, og det andre inkluderer i sin grunnlov en hel del og en annen desimal.

En "vanlig brøkdel" er uttrykket av en mengde fordelt mellom en annen, uten å gjøre denne divisjonen. Matematisk er en vanlig brøkdel et rasjonelt tall, som er definert som forholdet mellom to heltall "a/b", hvor b ≠ 0.

Et "desimaltall" er et tall som består av to deler: en hel del og en desimal del.

For å skille hele delen av desimaldelen, plasseres et komma, kalt desimal koma, selv om det også brukes et punkt.

Desimaltall

Et desimaltall kan ha en endelig eller uendelig mengde tall i desimaldelen. I tillegg kan den uendelige mengden desimaler deles inn i to typer:

Periodisk

Det vil si at det har et repetisjonsmønster. For eksempel 2.454545454545 ..

Ikke -periodisk

De har ikke noe repetisjonsmønster. For eksempel 1 7845265397219 ..

Tallene som har en periodisk mengde eller uendelig av desimaler, kalles rasjonelt tall, mens de som har en uendelig ikke -periodisk mengde, kalles irrasjonell.

Foreningen av settet med rasjonelle tall og settet med irrasjonelt antall er kjent som settet med reelle tall.

Forskjeller mellom vanlig brøkdel og desimaltall

Forskjellene mellom en vanlig brøkdel og et desimaltall er:

1- Desimaldel

Hver felles brøk har et begrenset antall tall i sin desimale del eller en periodisk uendelig mengde, mens et desimaltall kan ha en uendelig ikke -periodisk mengde tall i desimaldelen.

Ovennevnte sier at hvert rasjonelt tall (hver vanlig brøkdel) er et desimaltall, men ikke hvert desimaltall er et rasjonelt tall (en vanlig brøkdel).

2- Notasjon

Hver vanlig brøk er betegnet som forholdet mellom to heltall, mens et irrasjonelt desimaltall ikke kan betegnes på denne måten.

De mest brukte irrasjonelle desimaltallene i matematikk er betegnet med firkantede røtter (√ ), kubikk (³√ ) og øvre grader.

I tillegg til disse er det to veldig kjente tall, som er antall Euler, betegnet med E; Og PI -nummeret, betegnet med π.

Hvordan gå fra en felles brøk til et desimaltall?

For å gå fra en felles brøk til et desimaltall, er det bare nok for den tilsvarende divisjonen. For eksempel, hvis du har 3/4, er det tilsvarende desimaltallet 0,75.

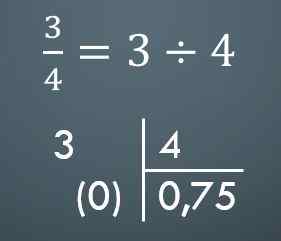
Hvordan gå fra et rasjonelt desimaltall til en felles brøkdel?

Den omvendte prosessen til den forrige kan også utføres. Følgende eksempel illustrerer en teknikk for å flytte fra et rasjonelt desimaltall til en felles brøk:

- La x = 1,78

Ettersom X har to desimaler, multipliseres den tidligere likheten med 10² = 100, som oppnår at 100x = 178; Og rydding x Det viser seg at x = 178/1. Dette siste uttrykket er den vanlige brøkdelen som representerer nummer 1.78.

Men kan denne prosessen gjøres for tall med en periodisk uendelig mengde desimaler? Svaret er ja, og følgende eksempel viser trinnene for å følge:

- La x = 2.193193193193 ..

Ettersom perioden for dette desimaltallet har 3 sifre (193), multipliseres det forrige uttrykket med 10³ = 1000, som oppnår uttrykket 1000x = 2193,193193193193 .. .

Det siste uttrykket blir nå trukket fra med den første og hele desimaldelen blir kansellert, og etterlater uttrykket 999x = 2191, hvor det oppnås at den vanlige brøkdelen er x = 2191/999.