Overflateekspansjonsformel, koeffisienter og eksempler

De overfladisk utvidelse Det er utvidelsen som oppstår når et objekt opplever variasjoner av overflaten på grunn av temperaturvariasjon. Det skyldes egenskapene til materialet eller dets geometriske form. Utvidelse dominerer i to dimensjoner i samme andel.

For eksempel i et ark, når det er en variant av temperaturen, er det overflaten til det samme som lider av den største endringen på grunn av termisk utvidelse.

Overflaten på en metallplate som vanligvis sees i gatene. Kilde: Pixabay.

Metallarket til forrige figur øker dets brede og dens lengde betydelig når det varmes opp ved solstråling. Tvert imot, begge avtar betydelig når de er avkjølt på grunn av en reduksjon i omgivelsestemperatur.

Det er av denne grunn at når fliser er installert i en etasje, skal noen kanter med andre ikke bli rammet, men det må være et separasjonsrom som kalles dilatasjonskort.

I tillegg er dette rommet fylt med en spesiell blanding som har en viss grad av fleksibilitet, og forhindrer at fliser sprekker på grunn av sterkt trykk som termisk utvidelse kan produsere.

[TOC]

Hva er overfladisk utvidelse?

I et solid materiale opprettholder atomer sine mer eller mindre faste relative posisjoner rundt et balansepunkt. På grunn av termisk omrøring svinger de imidlertid alltid rundt det.

Ved å øke temperaturen øker også termisk svingning og fører til at middels svingningsposisjoner endres. Dette er fordi koblingspotensialet ikke akkurat er parabolsk og har asymmetri rundt minimum.

Nedenfor er en figur som skisserer den kjemiske bindingsenergien avhengig av den interatomiske avstanden. Den totale svingningsenergien ved to temperaturer vises også og hvordan svingningssenteret beveger seg.

Det kan tjene deg: Pascal Tonel: Hvordan det fungerer og eksperimenter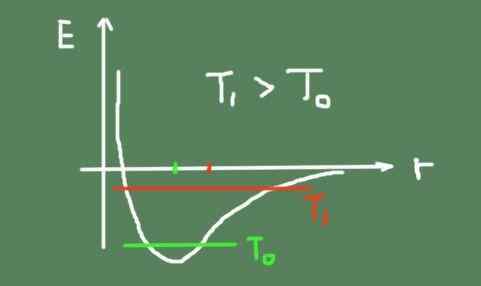Link Energy Graph kontra interatomisk avstand. Kilde: Selvlaget.

Overfladisk utvidelse og dens koeffisient

For å måle den overfladiske utvidelsen starter vi fra et innledende område A og en innledende temperatur T, av objektet som utvidelsen skal måles.

Anta at dette objektet er en lamina i område A, og tykkelsen på det er mye lavere enn kvadratroten til området a. Arket blir utsatt for en ΔT temperaturvariasjon, slik at den endelige temperaturen på den samme når den termiske balansen med varmekilden vil bli etablert vil være t '= t+ Δt.

Under denne termiske prosessen vil overflatearealet også ha endret seg til en ny verdi ved '= A + ΔA. Dermed er overflateutvidelseskoeffisienten σ definert som forholdet mellom den relative variasjonen av arealet per enhet for temperaturvariasjon.

Følgende formel definerer den overfladiske utvidelseskoeffisienten σ:

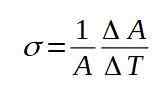
Den overfladiske utvidelseskoeffisienten σ er praktisk talt konstant for et bredt spekter av temperaturverdier.

På grunn av definisjonen av σ er dimensjonene omvendt temperatur. Som en enhet brukes den vanligvis ° C^-1.

Overflateutvidelseskoeffisient for forskjellige materialer

Neste gang vil vi gi en liste over den overfladiske utvidelseskoeffisienten for noen materialer og elementer. Koeffisienten beregnes i normalt atmosfæretrykk basert på en omgivelsestemperatur på 25 ° C, og dens verdi anses som konstant i et område på ΔT fra -10 ° C til 100 ° C.

Enheten for den overfladiske utvidelseskoeffisienten vil være (° C)^-1

- Stål: σ = 24 ∙ 10^-6 (° C)^-1

- Aluminium: σ = 46 ∙ 10^-6 (° C)^-1

Det kan tjene deg: magnetisering: orbital og spinn magnetisk øyeblikk, eksempler

- Gull: σ = 28 ∙ 10^-6 (° C)^-1

- Kobber: σ = 34 ∙ 10^-6 (° C)^-1

- Messing: σ = 36 ∙ 10^-6 (° C)^-1

- Jern: σ = 24 ∙ 10^-6 (° C)^-1

- Glass: σ = (14 til 18) ∙ 10^-6 (° C)^-1

- Kvarts: σ = 0,8 ∙ 10^-6 (° C)^-1

- Diamant: σ = 2 ,, 4 ∙ 10^-6 (° C)^-1

- Bly: σ = 60 ∙ 10^-6 (° C)^-1

- Eik tre: σ = 108 ∙ 10^-6 (° C)^-1

- PVC: σ = 104 ∙ 10^-6 (° C)^-1

- Karbonfiber: σ = -1,6 ∙ 10^-6 (° C)^-1

- Betong: σ = (16 til 24) ∙ 10^-6 (° C)^-1

De fleste materialer strekker seg med en temperaturøkning. Noen materialer som karbonfiber oppfyller imidlertid temperaturøkningen.

Løst eksempler på overfladisk utvidelse

Eksempel 1

En stålplate har dimensjoner på 3m x 5m. Om morgenen og i skyggen er temperaturen 14 ° C, men ved middagstid varmer solen den opp til 52 ° C. Finn det endelige området på platen.

Løsning

Vi starter fra definisjonen av overfladisk utvidelseskoeffisient:

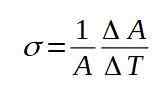
Herfra fjerner vi variasjonen i området:

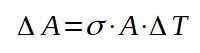
Vi fortsetter deretter med å erstatte de respektive verdiene for å finne økningen i området med temperaturøkningen.

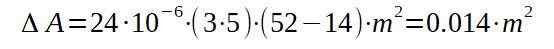
Det vil si at det endelige området vil være 15.014 kvadratmeter.

Eksempel 2

Vis at den overfladiske utvidelseskoeffisienten er omtrent det dobbelte av den lineære utvidelseskoeffisienten.

Løsning

Anta at vi starter fra en rektangulær plate med bredde dimensjoner lx og lang tid, da vil det opprinnelige området være en = lx ∙ ly

Kan tjene deg: termometriske skalaer

Når platen lider av en temperaturøkning ΔT, øker dimensjonene også den nye bredden Lx 'og dens nye' lange, slik at det nye området vil være en '= lx' ∙ ly '

Variasjonen som plateområdet har lidd på grunn av temperaturendring vil da være

Δa = lx '∙ ly' - lx ∙ ly

hvor lx '= lx (1 + α Δt) og ly' = ly (1 + α Δt)

Det vil si at endring av område avhengig av den lineære utvidelseskoeffisienten og temperaturendringen vil være:

Δa = lx (1 + α Δt) ∙ ly (1 + α Δt) - lx ∙ LY

Dette kan skrives om som:

Δa = lx ∙ ly ∙ (1 + α Δt) ² - lx ∙ ly

Utvikling av torget og multipliserer vi følgende:

Jeg

Som α er i størrelsesorden 10^-6, Ved å heve den firkantet er det ordren på 10^-12. Dermed er det kvadratiske uttrykket i det forrige uttrykket foraktelig.

Da kan økningen i området nærmer seg av:

Δa ≈ 2α Δt lx ∙ ly

Men økningen i området avhengig av den overfladiske utvidelseskoeffisienten er:

Δa = γ Δt a

Fra hvor et uttrykk utledes som relaterer den lineære utvidelseskoeffisienten til den overfladiske utvidelseskoeffisienten.

y ≈ 2 ∙ α

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mac Graw Hill. 422-527
2. Giancoli, d. 2006. Fysikk: Prinsipper med applikasjoner. 6. Utgave. Prentice Hall. 238-249.