Euclidian Distance Concept, Formula, Beregning, eksempel

De Euklidiansk avstand Det er et positivt tall som indikerer separasjonen som to punkter har i et rom der aksiomene og teoremene til euklidgeometri er oppfylt.

Avstanden mellom to punkter A og B av et euklidisk rom er lengden på vektoren AB Tilhører den eneste linjen som går gjennom disse punktene.

Figur 1 . Unidimensjonalt euklidisk rom dannet av linjen (OX). Flere punkter på dette rommet, deres koordinater og avstander vises. (Utarbeidet av Ricardo Pérez).

Plassen vi oppfatter og hvor vi beveger mennesker er et tredimensjonalt rom (3-D), der aksiomene og teoremene til euklidgeometri blir oppfylt. I dette rommet er to -dimensjonale underområder (planer) og en -dimensjonale (rette) (rette) underområder.

Euklidiske rom kan være av en dimensjon (1-D), todimensjoner (2-D), tre dimensjoner (3-D) eller N-dimensjoner (N-D).

Dette er punkter i det endimensjonale rommet x som tilhører den orienterte linjen (oksen), retningen fra eller til x er den positive adressen. For å lokalisere punktene på denne linjen, brukes det kartesiske systemet som består av å tildele hvert punkt på linjen et tall.

[TOC]

Formel

Den euklidianske avstanden D (A, B) er definert mellom punkt A og B, som ligger på en linje, for eksempel kvadratroten til kvadratet for forskjellene i X -koordinatene:

D (a, b) = √ ((xb - xa)^2)

Denne definisjonen garanterer at: avstanden mellom to punkter er alltid en positiv mengde. Og at avstanden mellom A og B er lik avstanden mellom B og A.

Figur 1 viser det endimensjonale euklidianske rommet dannet av linjen (OX) og flere punkter på den linjen. Hvert punkt har en koordinat:

Punkt A har XA -koordinat = 2.5, B koordinat XB = 4 og punktet C koordinat XC = -2.5

Det kan tjene deg: Frekvens sannsynlighet: Konsept, hvordan det beregnes og eksempler

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ ((2.5 - 4) 2) = 1.5

D (a, c) = √ ((-2.5 - 2.5) 2) = 5.0

Euklidiansk avstand i to dimensjoner

Det to -dimensjonale euklidrommet er et plan. Punktene til et euklidiansk plan oppfyller aksiomene til euklidgeometri, for eksempel:

- På to punkter passerer en enkelt linje. 

- Tre punkter på flyet danner en trekant hvis indre vinkler alltid tilsetter 180º.

- I et rektangel -trekant er kvadratet av hypotenusen lik summen av kvadratene på bena.

I to dimensjoner har et punkt X- og Y -koordinater. 

For eksempel har et punkt P koordinater (XP, YP) ​​og et punkt som koordinerte (XQ, YQ).

Euklidisk avstand mellom punkt P og Q er definert med følgende formel:

D (p, q) = √ ((xq - xp)^2 + (yq - yp)^2)

Det skal bemerkes at denne formelen tilsvarer Pythagoras teorem, som vist i figur 2.

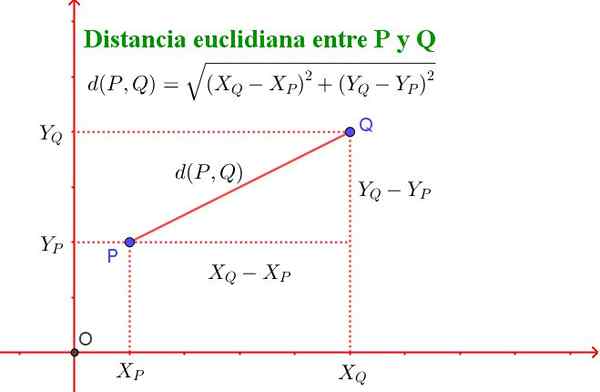Figur 2. Avstanden mellom to punkter P og Q av flyet møter Pythagoras teorem. (Utarbeidet av Ricardo Pérez).

Ikke -disklidianske overflater

Ikke alle to -dimensjonale rom møter euklidisk geometri. Overflaten på en sfære er et to -dimensjonalt rom.

Vinklene på en trekant på en sfærisk overflate tilsett ikke 180º, og med dette oppfyller ikke Pythagoras -teorem.

Euklidiansk avstand i n dimensjoner

Koordinatbegrepet kan utvides til større dimensjoner:

- I 2-D punkt har P koordinater (XP, YP)

- I 3-D et punkt som har koordinater (XQ, YQ, ZQ)

- I 4-D punkt R vil ha koordinater (XR, YR, ZR, WR)

- I N-D vil et punkt P ha koordinater (P1, P2, P3, ..., PN)

Kan tjene deg: Bars Graph: Egenskaper, hva er det for, eksempler

Avstanden mellom to P- og Q-punkter for et N-dimensjonalt euklidisk rom beregnes med følgende formel:

D (p, q) = √ ((q1 - p1)^2 +(q2 - p2)^2 +… +(qn - pn)^2)

Det geometriske stedet for alle punktene som i et n-dimensjonalt euklidisk rom som ekvidister fra et annet fast P-punkt (sentrum) danner en n-dimensjonal hyperfera.

Hvordan beregne den euklidianske avstanden

Nedenfor er avstanden mellom to punkter som ligger i det euklidiske tre -dimensjonale rommet beregnes.

Anta punkt A i kartesiske koordinater x, y, z gitt av A :( 2, 3, 1) og punkt B av koordinater B :( -3, 2, 2).

Du vil bestemme avstanden mellom disse punktene, som det generelle forholdet brukes til:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 *3) = 3 √ (3) = 5.196

Eksempel

Det er to punkter P og Q.  P -punktet for kartesiske koordinater x, y, z gitt av P :( 2, 3, 1) og punktet Q for koordinater Q :( -3, 2, 1).

Det blir bedt om å finne koordinatene til midtpunktet M for [PQ] -segmentet som forbinder de to punktene. 

Løsning:

Det antas at det ukjente punktet M har koordinater (x, y, z).

Ettersom m er gjennomsnittlig punkt for [pq], må det oppfylles at d (p, m) = d (q, m), så det må også oppfylles d (p, m)^2 = d (q, m)^ 2:

(X - 2)^2 + (y - 3)^2 + (z - 1)^2 = (x - (-3))^2 + (y - 2)^2 + (z - 1)^2

Som i dette tilfellet er den tredje termin den samme i de to medlemmene som det forrige uttrykket er forenklet til:

Kan tjene deg: absolutt konstant

(X - 2)^2 + (y - 3)^2 = (x + 3)^2 + (y - 2)^2 

Det er da en ligning med to ukjente x og y. En annen ligning er nødvendig for å løse problemet.

Punkt M tilhører linjen som passerer gjennom P- og Q -punktene, som vi kan beregne som følger:

Først er direktørvektoren Pq av linjen: Pq = = .

Deretter P.m = Op + til Pq, hvor Op Det er vektorposisjonen til punkt P og til Det er en parameter som tilhører reelle tall. 

Den forrige ligningen er kjent som vektorligningen til linjen, som i kartesiske koordinater vedtar som følger:

= + a =

Like de tilsvarende komponentene er:

X - 2 = 2 - 5 a; Og - 3 = 3 -a; Z - 1 = 0

Det vil si at x = 4 - 5a, y = 6 - a, endelig z = 1.

Det erstattes i det kvadratiske uttrykket som relaterer X til Y:

(4 - 5a - 2)^2 + (6 - a - 3)^2 = (4 - 5a + 3)^2 + (6 - A - 2)^2

Det er forenklet:

(2 - 5a)^2 + (3 -a)^2 = (7 - 5a)^2 + (4 - a)^2

Nå utvikler:

4 + 25 A^2 - 20a + 9 + A^2 - 6a = 49 + 25 A^2 - 70a + 16 + A^2 - 8a

Det er forenklet, og kansellerer lignende vilkår i begge medlemmene:

4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a

Parameter A:

52 A = 49 + 16 - 4 - 9 = 52 Resultat at a = 1.

Det vil si at x = 4 - 5, y = 6 - 1, endelig z = 1.

Endelig får vi de kartesiske koordinatene til midtpunktet m av segmentet [PQ]:

M: (-1, 5, 1).

Referanser

1. Lehmann c. (1972) Analytisk geometri. UTEHA.
2. Superprof. Avstand mellom to punkter. Gjenopprettet fra: Superprof.er
3. Unam. Avstand mellom relaterte sublineære varianter. Gjenopprettet fra: Prometheus.Matem.Unam.MX/
4. Wikipedia. Euklidiansk avstand. Gjenopprettet fra: er.Wikipedia.com
5. Wikipedia. Euklidisk rom. Gjenopprettet fra: er.Wikipedia.com