Domene og Conquominium av en funksjon (med eksempler)

Begrepene domene og motsetning av en funksjon De blir ofte undervist i beregningskursene som er undervist i begynnelsen av universitetskarrieren.

Før du definerer domene og motsetning, bør du vite hva en funksjon er. En F -funksjon er en korrespondanselov (regel) mellom elementene i to sett.

Hele hvor elementene er valgt, kalles funksjonen til funksjonen, og settet som disse elementene blir sendt gjennom F kalles Crissominium.

I matematikk er en funksjon med domene A og Conquominium B betegnet ved uttrykk F: A → B.

Det forrige uttrykket sier at elementene i sett A blir sendt til sett B etter korrespondanseloven f.

En funksjon tildeler hvert element i settet til et enkelt element i sett B.

Domene og motsetning

Gitt en reell funksjon av en reell variabel f ​​(x), må funksjonens domene være alle de reelle tallene slik at når det blir evaluert i F, er resultatet et reelt tall.

Generelt er motsetningen til en funksjon settet med virkelige n -tall. Motsetningen kalles også ankomst- eller codominium -settet med F -funksjonen.

Motsetningen til en funksjon er alltid r?

Nei. Så lenge funksjonen ikke studeres i detalj, blir settet med reelle n -tall vanligvis tatt som motsetning.

Men når funksjonen er studert, kan et mer passende sett tas som Conquominium, som vil være et undergruppe av r.

Det aktuelle settet som er nevnt i forrige avsnitt sammenfaller med bildet av funksjonen.

Definisjonen av bildet eller området for en funksjon f refererer til alle verdier som kommer fra å evaluere et element i domenet i f.

Domene og motsetningseksempler

I de følgende eksemplene, hvordan du beregner domenet til en funksjon og dets bilde er illustrert.

Eksempel 1

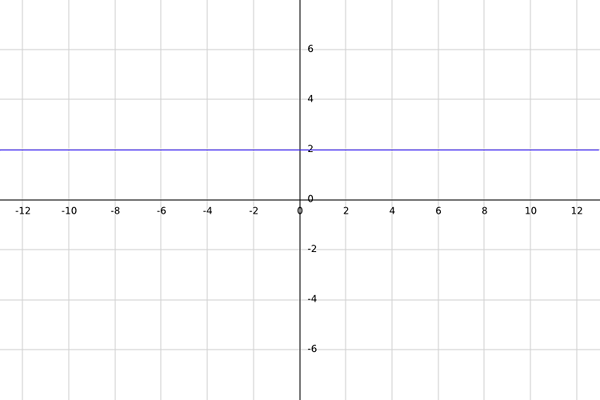
La f være en reell funksjon definert av f (x) = 2.

M -domenet til F er alle reelle tall slik at når de evaluerer dem i F, er resultatet et reelt tall. Motsetningen for øyeblikket er lik r.

Ettersom den gitte funksjonen er konstant (alltid lik 2), må den uansett hvilket reelt antall velges, siden når evaluering av det i F, vil resultatet alltid være lik 2, noe som er et reelt tall.

Derfor er domenet til den gitte funksjonen alle reelle tall; det vil si a = r.

Nå som det allerede er kjent at resultatet av funksjonen alltid er lik 2, er bildet av funksjonen bare nummer 2, derfor kan motsetningen til funksjonen omdefineres som b = img (f) = 2.

Derfor f: r → 2.

Eksempel 2

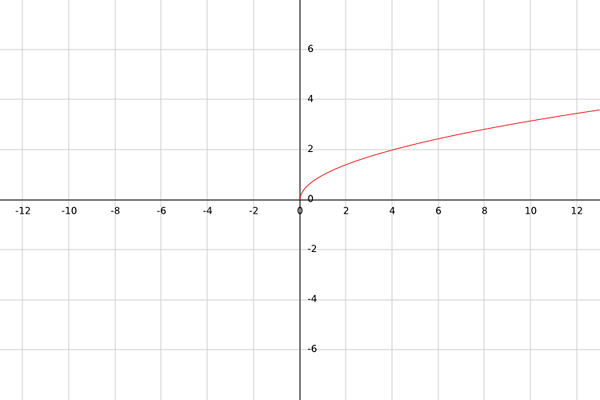
La g være en reell funksjon definert av G (x) = √x.

Så lenge bildet av G ikke er kjent, er Conspominium of G B = R.

Med denne funksjonen bør det tas i betraktning at firkantede røtter bare er definert for ikke -negative tall; det vil si for tall større enn eller lik enn null. For eksempel er √-1 ikke et reelt tall.

Derfor må mestring av G -funksjonen være alle tallene som er større enn eller lik enn null; det vil si x ≥ 0.

Derfor a = [0,+∞).

For å beregne området skal det bemerkes at ethvert resultat av G (x), fordi det er en kvadratrot, alltid vil være større enn eller lik. Det vil si B = [0,+∞).

Avslutningsvis, g: [0,+∞) → [0,+∞).

Eksempel 3

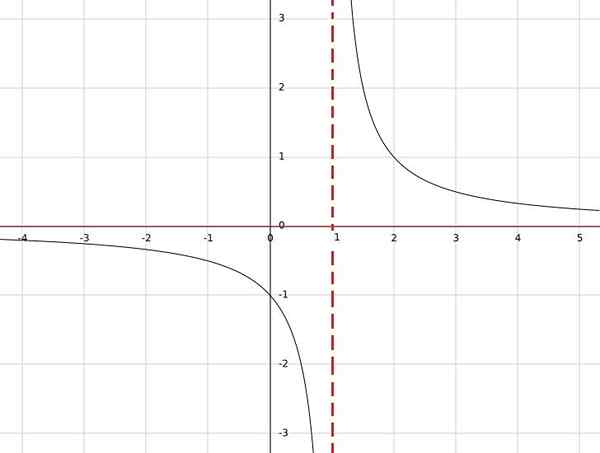
Hvis du har funksjonen h (x) = 1/(x-1), er denne funksjonen ikke definert for x = 1, siden i nevneren vil den oppnås null og divisjonen med null ikke er definert.

På den annen side, for enhver annen reell verdi, vil resultatet være et reelt tall. Derfor er domene alle reais bortsett fra en; det vil si a = r \ 1.

På samme måte kan det sees at den eneste verdien som ikke kan oppnås som et resultat er 0, siden en brøk er lik null må telleren være null.

Derfor er bildet av funksjonen settet med alle reais bortsett fra null, så blir det tatt som Conquominium B = R 0.

Avslutningsvis h: r \ 1 → r \ 0.

Observasjoner

Domene og bilde trenger ikke å være det samme settet, som demonstrert i eksempler 1 og 3.

Når en funksjon er graf i det kartesiske plan.