Arrhenius ligning
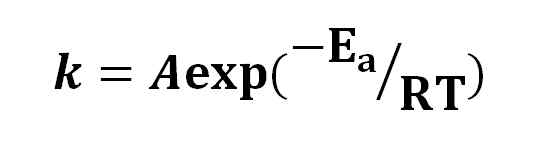
- 3510
- 482
- Theodor Anders Hopland
Hva er Arrhenius -ligningen?
De Arrhenius ligning Det er en tilnærming som relaterer hastighetskonstanten til en kjemisk reaksjon avhengig av temperatur. Det ble opprettet i 1899 av den svenske kjemikeren Svante Arrhenius (1859-1927). Representerer et av de mest grunnleggende bidragene i utviklingen av kjemisk kinetikk.
Denne ligningen skylder sine teoretiske baser til mange forskere, inkludert Wihelmy (1850), Berthelot (1862) og J. J. Hood (1885). Men den største innflytelsen tilskrives opprettelsen av Arrhenius -ligningen til arbeidet utført av Van't Hoof (1884), som etablerte en avhengighet av likevektskonstantene til de kjemiske reaksjonene med temperaturen.
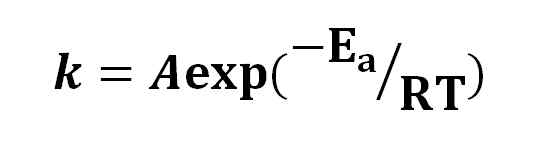 Arrhenius ligning. Kilde: Gabriel Bolívar.
Arrhenius ligning. Kilde: Gabriel Bolívar. Basert på Arrhenius -ligningen har ideen om at en økning på 10 ºC har forårsaket en duplisering av reaksjonshastigheten blitt formidlet. Andre tolkninger som blir det er at molekyler trenger litt aktiveringsenergi for å reagere på hverandre.
På samme måte påpekes det at Arrhenius -ligningen er en annen form for eksponentiell oppløsning der verdien av hastighetskonstanten avhengig av eksponenten -etil/RT, hvor etil er aktiveringsenergi.
Ligning og forklaring
Arrhenius -ligningen har følgende to uttrykk:
K = ae-Ea/rt
Form av ligningen som brukes i kjemi og er relatert til reagensmol.
K = ae-Ea/kbt
Form av ligningen som brukes i fysikk og er relatert til flere molekyler, enn med føflekker.
Begge stammer fra Van´ HOOF -ligningen for variasjonen av likevektskonstanten K avhengig av temperaturen. Base -ligningen er:
d (ln k)/dt = etil/Rt2
Det kan tjene deg: Dibenzalacetona: egenskaper, reaksjonsmekanisme, bruksområder, risikoSom er integrert under forutsetning av dettil er uavhengig av temperatur. Så vi har:
ln k = - etil/RT + ln a
Hvor ln a er integrasjonskonstanten. Når den eksponentielle funksjonen brukes på begge sider av ligningen, oppnår vi Arrhenius -ligningen som allerede er introdusert.
Komponenter
k
Det er hastighetskonstanten til en kjemisk reaksjon. Verdien kan oppnås, i tillegg til bruken av Arrhenius -ligningen, ved anvendelse av hastighetsloven. Representerer antall kollisjoner mellom partikler produsert av en reaksjon per sekund.
TIL
Det er den såkalte pre-eksponentielle faktoren, som representerer hyppigheten av kollisjoner mellom reagensmolekyler med en passende geometrisk orientering som kanskje eller ikke kan gi en kjemisk reaksjon. Hvis temperaturvariasjonen er av liten styrke, blir den vanligvis tatt som konstant. Denne faktoren har sin egen formel:
A = z ρ
Der Z er kjent som en frekvens- eller kollisjonsfaktor, og ρ den geometriske eller steriske faktoren som indikerer den relative orienteringen av molekylene ved kollisjonspunktet. Den konstante A har de samme enhetene som hastighetskonstanten. I tilfelle at det ikke er noen aktiveringsenergi, vil størrelsen på A være lik den for k.
OGtil
Det er aktiveringsenergien, som representerer terskelenergien før du når overgangen stat.
Aktiveringsenergi har KJ/mol -enheten. Men i beregningene brukes j/mol som en enhet. Det minste (-) tegnet som går foran etil, Det tjener til å indikere at økningen gir en reduksjon i reaksjonshastighet, så vel som reduksjonen gir en økning i reaksjonshastigheten.
Kan tjene deg: gasskromatografiRt
Representerer den gjennomsnittlige kinetiske energien. I mellomtiden er R den universelle konstanten av gasser, og er en av dens mest brukte verdier 8.31 J · K-1· Mol-1. Og T er den absolutte temperaturen uttrykt i Kelvin (k).
og
Det er grunnlaget for naturlige eller neperiske logaritmer, med en verdi av 2.71828.
og-Ea/rt
Det er brøkdelen av å reagere molekyler med lik eller overflødig energi i forhold til aktiveringsenergi.
applikasjoner
De fleste av anvendelsene av Arrhenius -ligningen kommer fra bruk i bestemmelse hastighetskonstanten; og i forlengelse av reaksjonen, så vel som aktiveringsenergien.
For eksempel er det utviklet en kjemisk modell basert på Arrhenius -ligningen, som kan forutsi egenskapene til materialene som deres temperaturendring, og brukes innen geologi, konstruksjon, prosjektering av materialer og i matvitenskap.
Det har blitt brukt, selv om Arrhenius -ligningen med viss kritikk i kinetikken til faststoffreaksjoner. Det har også blitt brukt til å karakterisere planters svar på vannstress.
Arenhius -ligningen fungerte som grunnlag for å skape en matematisk modell, som kvantifiserer effekten av temperaturen på levetiden til nikkelmetalliske hydridceller eller batterier.
På samme måte, basert på Arrhenius -ligningen, ble nedbrytningshastigheten for svineavfall og kokeolje etablert, under forskjellige fuktighetsinnhold.
Løste øvelser
Oppgave 1
Hva er aktiveringsenergien til en reaksjon hvis det blir funnet at dens hastighetskonstante tredobler når temperaturen stiger fra 600 K til 610 K?
Kan tjene deg: fenoksyeddiksyre: syntese, prosedyre, bruk, risikoStarter fra Arrhenius -ligningen:
k = a · e-Ea/rt
Vi fjerner faktoren A:
A = k1 / (e-EA/RT1)
Men siden vi har to temperaturer, t1 og T2, Det vil være to hastighetskonstanter: k1 og k2. Faktor A endres ikke, så vi kan matche det for den andre temperaturen:
k1 / (e-EA/RT1) = k2 / (e-EA/RT2)
Og rydding etil vi vil ha:
OGtil = R (ln k2/k1) / (1 / t1 - 1/t2)
Som hva2 er tre ganger større enn k1,
k2 / k1 = 3
LN (3) = 1.099
Og på den annen side:
1 / t1 = 1/600 K = 1.66 x 10-3 K-1
1 / t2 = 1 /610 K = 1.64 x 10-3 K-1
Erstatning da:
OGtil = (8.31 J · K-1· Mol-1) (1.099) / (1.66 x 10-3 K-1 - 1.64 x 10-3 K-1)
= 456.5 kJ · mol-1
Oppgave 2
I en gassfase -reaksjon er aktiveringsenergien lik 103 kJ/mol, og hastighetskonstanten er 0.085 min-1. Beregn hastighetskonstanten ved 323 K.
Fra forrige uttrykk fjerner vi ln k2/k1:
ln k2/k1 = (Etil/R) (1 /t1 - 1/t2)
Utvikle den rette delen av ligningen:
ln k2/k1 = (103.000 J · mol-1 / 8.31 J · K-1· Mol-1) (1/273 K - 1/323 K)
ln k2/k1 = 6.99
Tar antilogaritmer:
k2/k1 = 1.086
k2 = (k1) (1.086)
= (0.085 min-1) (1.086)
= 0.092 min-1
Referanser
- Whitten, Davis, Peck & Stanley. (2008). Kjemi. (8. utg.). Cengage Learning.
- Walter J. Moore. (1963). Fysisk kjemi. I kjemisk kinetikk. Fjerde utgave, Longmans.
- Iran. Levine. (2009). Prinsipper for fysikjemi. Sjette utgave. Mc Graw Hill.
- Wikipedia. (2020). Arrhenius ligning. Hentet fra: i.Wikipedia.org
- Guenevieve del Mundo et al. (10. september 2020). Arrhenius ligning. Gjenopprettet fra: Chem.Librettexts.org
- Clark Jim. (2013). Rate Constants og Arrhenius -ligningen. Gjenopprettet fra: Chemguide.co.Storbritannia
- Redaktørene av Enyclopaedia Britannica. (2020). Arrhenius ligning. Gjenopprettet fra: Britannica.com
- Helmestine, Anne Marie, PH.D. (28. august 2020). Arrhenius ligningsformel og eksempel. Gjenopprettet fra: Thoughtco.com

