Polynomiske ligninger

Hva er polynomligninger?

De Polynomiske ligninger De er en uttalelse som reiser likheten mellom to uttrykk eller medlemmer, der minst ett av begrepene som utgjør hver side av likhet er polynomer p (x). Disse ligningene er navngitt i henhold til graden av variablene deres.

Generelt er en ligning en uttalelse som etablerer likheten mellom to uttrykk, hvor det i minst en av disse er ukjente mengder, som kalles variabler eller ukjente. Selv om det er mange typer ligninger, er disse generelt klassifisert i to typer: algebraisk og transcendent.

Polynomiske ligninger inneholder bare algebraiske uttrykk, som kan ha en eller flere ukjente som griper inn i ligningen. I henhold til eksponenten (karakteren) som de har, kan de klassifiseres som: første klasse (lineær), andre klasse (kvadratisk), tredje klasse (kubikk), fjerde klasse (kvantikk), grad større enn eller lik fem og irrasjonell.

Kjennetegn på polynomligninger

Polynomiske ligninger er uttrykk som dannes av en likhet mellom to polynomer; Det vil si for de endelige summeret av multiplikasjoner mellom verdier som er ukjente (variabler) og faste tall (koeffisienter), der variablene kan ha eksponenter, og verdien deres kan være et positivt heltall, inkludert null.

Eksponenter bestemmer graden eller type ligning. Det uttrykket som har mest verdieksponent vil representere den absolutte graden av polynom.

Polynomiske ligninger er også kjent som algebraisk, koeffisientene deres kan være reelle eller komplekse tall og variablene er ukjente tall representert med en bokstav, for eksempel: "x".

Hvis ved å erstatte en verdi med variabelen "x" i P (x) er resultatet lik null (0), sies det at denne verdien tilfredsstiller ligningen (det er en løsning), og kalles generelt den polynomiske rot.

Når en polynomligning utvikles, ønsker alle røtter eller løsninger å bli funnet.

Typer polynomligninger

Det er flere typer polynomligninger, som er differensiert i henhold til antall variabler, og også i henhold til graden av deres eksponent.

Dermed er polynomligningene -der den første begrepet er et polynom som bare har en ukjent, med tanke på at graden kan være et hvilket som helst naturlig tall (n) og den andre termen er null -kan uttrykkes som følger:

Kan tjene deg: Historie med trigonometri fra dens opprinnelse

til_{N *} xⁿ + til_{N-1 *} x^N-1 +… + A_{1 *} x¹ + til_{0 *} x₀ = 0

Hvor:

• til_n, til_N-1 allerede₀, De er ekte koeffisienter (tall).
• til_n er forskjellig fra null.
• Eksponent n er et positivt heltall som representerer graden av ligning.
• x er den variabelen eller det ukjente som må søkes.

Den absolutte eller større graden av en polynomligning er den eksponenten av større verdi blant alle de som danner polynom; På denne måten klassifiseres ligninger som:

Første klasse

Den første grads polynomligninger, også kjent som lineære ligninger, er de som graden (den største eksponenten) er lik 1, polynomet er av formen P (x) = 0; Og det er sammensatt av en lineær og et uavhengig begrep. Det er skrevet som følger:

AX + B = 0.

Hvor:

• A og B er reelle tall og a ≠ 0.
• Øks er det lineære begrepet.
• B er det uavhengige begrepet.

For eksempel ligning 13x - 18 = 4x.

For å løse lineære ligninger, må alle begrepene som inneholder det ukjente X overføres til siden av likhet, og de som ikke har bevegelse på den andre siden, for å fjerne den og få en løsning:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

På denne måten har den gitte ligningen bare en løsning eller rot, som er x = 2.

Andre klasse

Andre grads polynomligninger, også kjent som kvadratiske ligninger, er de der graden (den største eksponenten) er lik 2, polynomet er av formen p (x) = 0, og er sammensatt av et kvadratisk begrep, a lineær og en uavhengig. Det uttrykkes som følger:

øks² + BX + C = 0.

Hvor:

• a, b og c er reelle tall og a ≠ 0.
• øks² Det er det kvadratiske uttrykket, og "A" er koeffisienten for det kvadratiske uttrykket.
• BX er det lineære begrepet, og "B" er koeffisienten for det lineære begrepet.
• C er det uavhengige begrepet.

Oppløsning

Generelt gis løsningen på denne typen ligninger når du rydder X i ligningen, og forblir som følger, som kalles et oppløsningsmiddel:

Kan tjene deg: binomial teorem

Der, (b² - 4AC) kalles diskriminering fra ligningen, og dette uttrykket bestemmer antall løsninger som ligningen kan ha:

• Ja (b² - 4ac) = 0, vil ligningen ha en enkelt løsning som er dobbelt; det vil si at det vil ha to like løsninger.
• Ja (b² - 4ac)> 0, vil ligningen ha to forskjellige virkelige løsninger.
• Ja (b² - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

For eksempel har du 4x -ligningen² + 10x - 6 = 0, for å løse det først blir begrepene A, B og C identifisert, og deretter erstattes det i formelen:

A = 4

B = 10

C = -6.

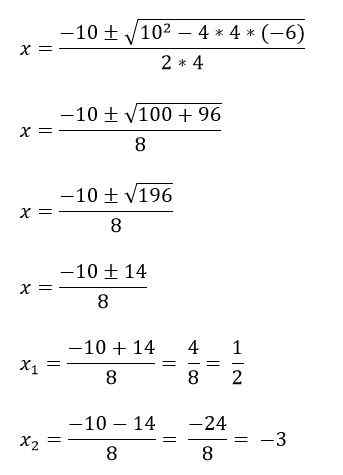
Det er tilfeller der andre -graders polynomligninger ikke har de tre begrepene, og det er derfor de løses annerledes:

• I tilfelle kvadratiske ligninger ikke har det lineære begrepet (det vil si B = 0), vil ligningen uttrykkes som AX² + C = 0. For å løse det, blir X ryddet² Og de firkantede røttene brukes i hvert medlem, og husker at de to mulige tegnene som det ukjente kan ha:

øks² + C = 0.

x² = - C ÷ a

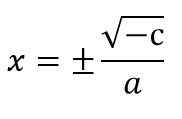
For eksempel 5 x² - 20 = 0.

5 x² = 20

x² = 20 ÷ 5

X = ± √4

x = ± 2

x₁ = 2.

x₂ = -2.

• Når den kvadratiske ligningen ikke har et uavhengig begrep (det vil si C = 0), vil ligningen uttrykkes som AX² + BX = 0. For å løse det, må den vanlige faktoren til det ukjente X tas i det første medlemmet; Ettersom ligningen er tilpasset null, blir den oppfylt at minst en av faktorene vil være lik 0:

øks² + BX = 0.

x (øks + b) = 0.

På denne måten må du:

x = 0.

x = -b ÷ a.

For eksempel: du har ligning 5x² + 30x = 0. Først er det faktor:

5x² + 30x = 0

x (5x + 30) = 0.

To faktorer genereres som er x y (5x + 30). Den ene av disse vil bli betraktet som null, og den andre får løsning:

x₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

x₂ = -6.

Høyeste karakter

Hovedgraden polynomligninger er de som spenner fra tredje klasse og fremover, som kan uttrykkes eller løses med den generelle polynomligningen i noen grad:

Kan tjene deg: Korrelasjonskoeffisient: Formler, beregning, tolkning, eksempel

til_{N *} xⁿ + til_{N-1 *} x^N-1 +… + A_{1 *} x¹ + til_{0 *} x₀ = 0

Dette brukes fordi en ligning med en grad større enn to er resultatet av faktoriseringen av et polynom; Det vil si at det uttrykkes som multiplikasjon av grad en eller større polynomer, men uten reelle røtter.

Løsningen av denne typen ligninger er direkte, fordi multiplikasjonen av to faktorer vil være lik null hvis noen av faktorene er null (0); Derfor må hver av de polynomiske ligningene som er funnet løses, og samsvarer med hver av faktorene til null.

For eksempel har du tredje grads ligning (kubikk) x³ + x² +4x + 4 = 0. For å løse det må du følge følgende trinn:

• Vilkårene er gruppert:

x³ + x² +4x + 4 = 0

(x³ + x² ) + (4x + 4) = 0.

• Medlemmene bryter sammen for å få den vanlige faktoren til det ukjente:

x² (x + 1) + 4 (x + 1) = 0

(x² + 4)_*(x + 1) = 0.

• På denne måten oppnås to faktorer, som må være lik null:

(x² + 4) = 0

(x + 1) = 0.

• Det kan sees at faktoren (x² + 4) = 0 vil ikke ha en reell løsning, mens faktoren (x + 1) = 0 ja. Derfor er løsningen:

(x + 1) = 0

x = -1.

Løste øvelser

Løs følgende ligninger:

Første trening

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Løsning

I dette tilfellet uttrykkes ligningen som multiplikasjon av polynomer; det vil si at det er faktorisert. For å løse det, må hver faktor være lik null:

2x² + 5 = 0, har ingen løsning.

x - 3 = 0

x = 3.

1 + x = 0

x = - 1.

På denne måten har den gitte ligningen to løsninger: x = 3 og x = -1.

Andre trening

x⁴ - 36 = 0.

Løsning

Det ble gitt et polynom, som kan påskrives som en forskjell i firkanter for å nå en raskere løsning. Dermed gjenstår ligningen:

(x² + 6)_*(x² - 6) = 0.

For å finne løsningen av ligningene er begge faktorene lik null:

(x² + 6) = 0, har ingen løsning.

(x² - 6) = 0

x² = 6

x = ± √6.

Dermed har den innledende ligningen to løsninger:

x = √6.

x = - √6.