Ellipse

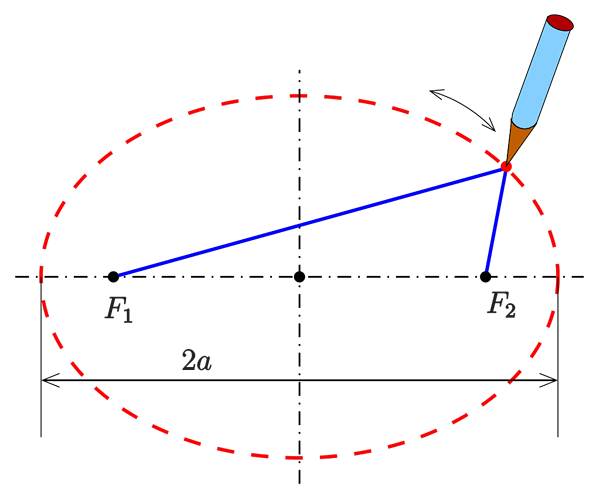
Figur 1. Gartnermetode for å tegne en ellipse. Summen av avstandene mellom et punkt P av ellipsen (i rødt) og søkelysene (i svart), forblir konstant. Kilde: AG2GAEH, CC BY-SA 4.0, via Wikimedia Commons.

Hva er en ellipse?

En ellipse er et sett med koordinatpunkter (x, y), som summen av avstandene til to faste punkter, kalt Focos, det er konstant. På sin side er søkelysene atskilt fra hverandre en avstand lik 2C.

Ellipene finnes i naturen. For eksempel er det i jordens bevegelse rundt solen, siden som demonstrert av tysk astronom.

I tillegg finnes den elliptiske formen i utformingen av arkitektoniske konstruksjoner, er en del av en medisinsk behandling for å ødelegge nyreberegninger og tjener til å forme forskjellige gjenstander som tanker og andre containere.

I den øvre figuren vises en ellipse med sine to søkelys, lokalisert like fra midten av figuren og på den lengste aksen. Tilstanden om at et punkt P må møte for å tilhøre ellipsen er at summen av avstandene til hvert fokus er fikset:

d₁ + d₂ = konstant.

Derfor, når en gartner vil. Ta deretter et tau av god størrelse, bind endene til innsatsen og støtt en pinne på tauet skyver den på den for å markere den elliptiske rillen på den myke jorden. Dette er Gartnermetode Å tegne ellipser.

Elipseelementer

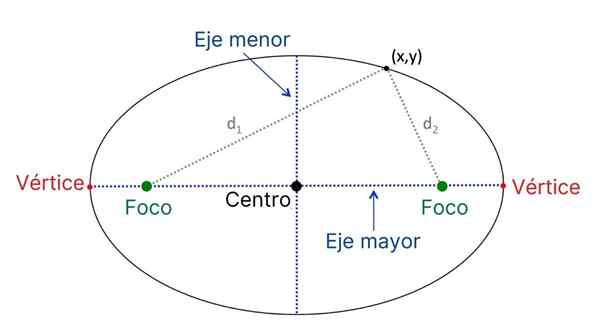Hovedelementer i en ellipse

Dette er hovedelementene i Ellipse:

1. Focos, Faste punkter som ligger på den lengste aksen til ellipsen.
2. Hjørner, De er de to punktene i ellipsen som linjen passerer som blir med i søkelysene.
3. Major Axis, Det er tauet som blir med i toppunktene og også inneholder søkelysene.
4. Senter, Mellompunkt for hovedaksen, som tilsvarer koordinatpunktet (h, k). Hvert fokus er like fra sentrum og på avstand c av det samme.
5. Mindre akse, Det er tauet som går gjennom sentrum og er vinkelrett på hovedaksen.
6. Vektorradioer, segmenter som forener hvert fokus med en p av ellipsen.
7. Fokalakse, rett som søkelysene er.
8. Fokalavstand, Det er avstanden mellom søkelysene, betegnet som 2C.
9. Sekundær akse, Axis vinkelrett på hovedaksen, som samtidig er mediatrix av segmentet som binder seg til søkelysene.
10. Symmetry Center, Punkt sammenfallende med sentrum av ellipsen, der symmetriaksene er krysset krysset.
11. Symmetriakser, linjer som inneholder de største og mindre aksene til ellipsen.

Kan tjene deg: beskatning

Typer ellipse

Det er to typer ellipse:

• De som har hovedaksen horisontalt.
• De som har den største vertikale aksen.

Da beskrives de matematisk:

Ellipse med den viktigste horisontale aksen

La punkt C koordinater (h, k) sentrum av ellipsen, lengden på hovedaksen er 2a og lengden på den mindre aksen lik 2b, med en> b.

Ligningen for denne ellipsen er:

Ellipse med den viktigste vertikale aksen

Med de samme parametrene for ellipsen med en horisontal akse, er ellipsen med den viktigste vertikale aksen skrevet som:

I begge tilfeller avstanden fra fokuset til sentrum c Det er relatert til sedimentene hoved- og mindreårig gjennom:

c² = a² - b²

Eksempler på ellipser

Horisontal ellipse

Følgende bilde viser en ellipse hvis hovedakse er horisontal. Senteret er på punkt (0,0) og søkelysene i henholdsvis (-3,0) og (3.0). Punkt P (0, -4) uthevet tilhører ellipsen.

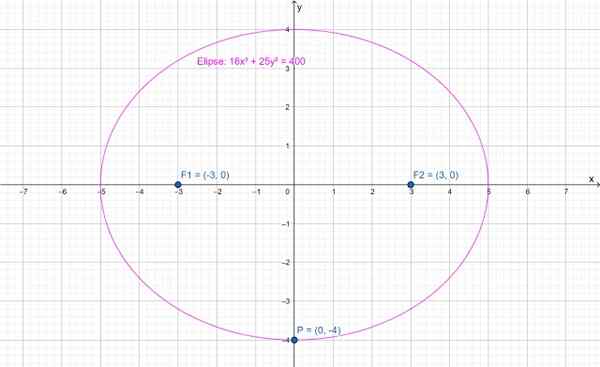Figur 2.- Ellipse hvis hovedakse er horisontal. Kilde: f. Zapata gjennom Geogebra.

Ligningen for denne ellipsen er:

16x² + 25 og² = 400

Det er ikke vanskelig å uttrykke denne ligningen i den kanoniske formen, det er nok til å dele alle vilkårene mellom 400 og forenkle praktisk (se øvelsen løst senere).

Vertikal ellipse

Følgende er en vertikal ellipse, hvis hovedakse sammenfaller med aksen og. Det er fokusert på punkt (0,0) og ligningen er:

36x² + 9y² = 324

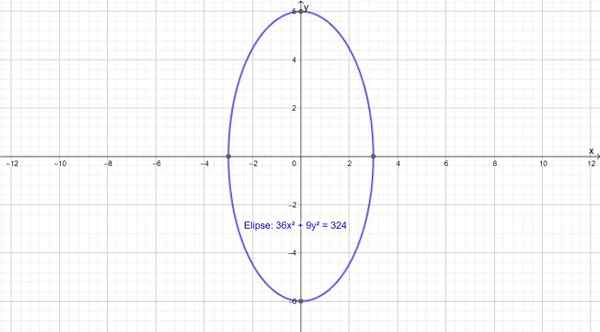Figur 3.- En ellipse med den viktigste vertikale aksen. Kilde: f. Zapata gjennom Geogebra.

Refleksjonseiendom

Den består av følgende: Hvis en reflektor eller en lydkilde er plassert i en av ellipse -søkelysene, gjenspeiles de utsendte bølgene mot det andre fokuset. Det er en god måte å omdirigere bølgene der energien din er nødvendig.

Kan tjene deg: Endecagon

Det er grunnen til at i de elliptiske hallene, når en person snakker å være i en av søkelysene, lytter en lytter som ligger i den andre fokuset tydelig.

Og i medisin brukes denne refleksjonsegenskapen til å ødelegge nyrestein ved å sette pasienten i en av søkelysene i et elliptisk kar fullt av vann, mens ultralydbølggeneratoren er plassert i det andre fokuset. Bølgene gjenspeiles i beregningene og fragmenterer dem i mindre partikler, som deretter blir utvist gjennom urinen.

Ska -radioen

Dette radioteleskopet er det største i sin type og forventes å begynne å jobbe i 2021. Overflaten er 1 km firkant, og det er derfor den kalles ska (på engelsk er de forkortelsen for Kvadratkilometer).

Ved å dra nytte av refleksjonsegenskapen til ellipsen, består strukturen av et arrangement på 3000 antenner med elliptisk form på omtrent 15 m bred, fordelt mellom Australia og Sør -Afrika. Med dette instrumentet, 50 ganger mer følsomt enn de som er i bruk akkurat nå, forventes det å ta en titt på universet når det fremdeles var mye yngre: omtrent en milliard år knapt.

Figur 4.- Kunstnerisk tolkning av ska radio ska. Kilde: Wikimedia Commons.

Trening løst

Finn de kanoniske ligningene til ellipene vist i figur 2 og 3, og i hvert tilfelle bestemmer lengdene på sansene større og mindre, så vel som fokale avstander.

Løsning

For den horisontale ellipsen, hvis ligning er 16x² + 25 og² = 400, alle vilkår mellom 400 er delt, noe som resulterer:

Kan tjene deg: Cotangent avledet: beregning, demonstrasjon, øvelser

 Som er forenklet:

Semi -aksen “A” måler 5 og den minste “B” måler 4, som også blir advart ved å observere bildet nøye. Når det gjelder brennskapsavstanden, må du:

c² = a² - b²

c² = 25 - 16 = 9 ⇒ C = √9 = 3

Derfor er C = 3 avstanden mellom sentrum og en av søkelysene. Begge fokusene er en avstand 2C = 6.

Når det gjelder den vertikale ellipsen 36x² + 9y² = 324 du har:

Ved å forenkle:

c² = 36 - 9 = 27

C = √27 ≅ 5.2

Derfor er avstanden mellom søkelysene 10.4 enheter.

Referanser

1. Hoffman, J. Valg av matematikkproblemer. Volum 3.
2. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
3. Universformler. Ellipsen. Gjenopprettet fra: Universoformulas.com.
4. Wikipedia. Kvadratkilometer. Gjenopprettet fra: er.Wikipedia.org.
5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.