Kutte innsatsen hvordan det blir beregnet og løse øvelser

Det er kjent som ren styrke som skyldes å bruke to krefter parallelt med et område og i motsatt retning. På denne måten kan et objekt deles inn i to deler, noe som får seksjonene til å gli en over en annen.

Daglige direkte skjæringsspenninger på stoffer, papirer eller metaller, utøvd av saks, guillotiner eller skjær. De vises også i strukturer som bolter eller skruer, pinner, bjelker, kiler og sveiser.

Figur 1. Med en saks gjøres en skjærinnsats. Kilde: Pixabay

Det er nødvendig å avklare at det ikke alltid er ment å dele eller kutte, men skjærinnsatsen har en tendens til å deformere objektet det brukes på; Det er grunnen til at bjelkene utsettes for å kutte innsatsen har en tendens til å kombinere med sin egen vekt. Følgende eksempler tydeliggjør poenget.

Figur 2 viser et enkelt skjema for å illustrere ovennevnte. Det er et objekt som to krefter virker i motsatte retninger. Det er et tenkt skjæreplan (det er ikke trukket) og styrkene virker på hver side av flyet, og skjærer i to stangen.

Når det.

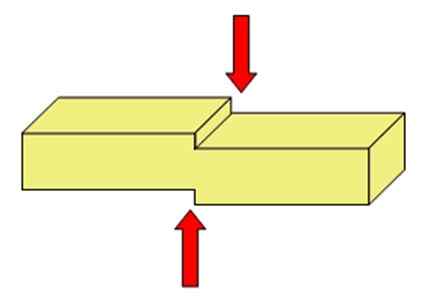Figur 2. De to kreftene som vises utøver en innsats som har en tendens til å skille stangen i to. Kilde: ADRE-ES [CC BY-SA 4.0 (https: // creativecommons.Org/lisenser/by-SA/4.0)] [TOC]

Kuttingsinnsats kan forårsake deformasjon

Du kan prøve å utøve en skjærinnsats ved å skyve hånden på lokket i en lukket bok. Det andre lokket må forbli fast på bordet, som kan oppnås ved å støtte den frie hånden slik at det ikke beveger seg. Boken vil deformere litt med denne handlingen, som skjematisert i følgende figur:

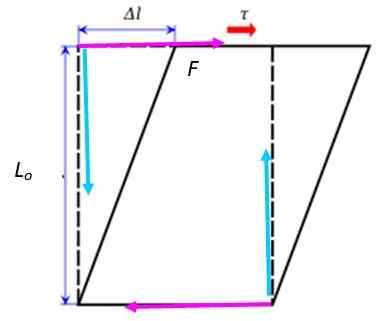Figur 3. Når du bruker en skjærinnsats på boken, er det en deformasjon. Kilde: Krishnavedala [CC0]

Hvis denne situasjonen blir analysert nøye, er de to kreftene som allerede er referert til, men denne gangen ble brukt horisontalt (I Fuchsia). Den ene er hånden hans på det ene ansiktet, og det andre blir brukt av overflaten av bordet på motsatt side av boken som er løst.

Kan tjene deg: treghet

Boken snur ikke, selv om disse kreftene kan forårsake et dreiemoment eller netto øyeblikk. For å unngå dette er de to andre vertikale kreftene (i turkis); Den som ble brukt med den andre hånden og den normale som ble utøvd ved bordet, hvis netto øyeblikk virker i motsatt retning som forhindrer rotasjonsbevegelsen.

[TOC]

Hvordan beregnes skjærinnsatsen?

Å kutte innsatsen vises til og med inne i menneskekroppen, siden blodet når sirkulær kontinuerlig utøver tangentielle krefter på det indre ansiktet av blodkarene, og forårsaker små deformasjoner i veggene.

Det er viktig å bestemme mulighetene for en manglende mislykkede. Ved å kutte innsatsen tas ikke bare styrken i betraktning, men også området den fungerer.

Dette forstås umiddelbart når du tar to sylindriske stenger med samme lengde, laget med samme materiale, men av forskjellig tykkelse og utsetter dem for å øke innsatsen til de går i stykker.

Det er klart at de nødvendige kreftene vil være veldig forskjellige, fordi den ene baren er tynnere enn den andre; Imidlertid vil innsatsen være den samme.

Skjærinnsatsen er betegnet med den greske teksten τ (tau) og beregnes som forholdet mellom størrelsen på den påførte kraften F og området TIL av overflaten den virker på:

τ_gjennomsnitt= F /a

Innsatsen som således beregnes er den som produserer en gjennomsnittlig kraft på den aktuelle overflaten, siden styrken ikke virker på et unikt punkt på overflaten, men distribuert over hele den og ikke på en jevn måte. Fordelingen kan imidlertid representeres av en resulterende kraft som virker på et bestemt punkt.

Det kan tjene deg: blokker algebra: elementer, eksempler, løste øvelser

Dimensjonene til skjærspenningen er av kraft på overflaten. I enheter av det internasjonale systemet tilsvarer Newton/Metro Square, enheten kalt Pascal og forkortet PA.

De er de samme trykkenhetene, derfor enhetene i det engelske systemet som pund -fuerza/kake ² og Vågen-fuerza /tomme² De er også passende.

Kutte innsats og deformasjon

I mange situasjoner er størrelsen på skjærspenningen proporsjonal med den enhetlige deformasjonen forårsaket i objektet, for eksempel boken til forrige eksempel, som vil komme tilbake til de opprinnelige dimensjonene så snart hånden er fjernet. I så fall:

Ren styrke ∝ Unitary Deformation

Proporsjonalitetskonstanten i dette tilfellet er skjæringsmodul, stivhetsmodul eller skjærmodul (G):

Kutteinnsats = hør modul x enhetsdeformasjon

τ = g. γ

Med γ = ΔL/l_enten, Hvor ΔL Det er forskjellen mellom den endelige lengden og den første. Ved å kombinere de gitte ligningene kan et uttrykk for deformasjonen forårsaket av innsatsen finnes:

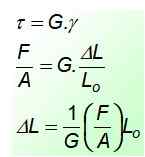
Verdien av konstanten G Det finnes i tabeller og enhetene er de samme som innsatsen, med tanke på at enhetsdeformasjonen er dimensjonsløs. Nesten alltid verdien av G er halv eller tredjedel av verdien av OG, Elastisitetsmodulen.

De er faktisk relatert ved uttrykk:

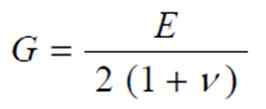
Hvor v er Poisson -modulen, en annen elastisk konstant av materialet hvis verdi er mellom 0 og ½. Derfor er G på sin side mellom E/3 og E/2.

Løste øvelser

-Oppgave 1

For å slå sammen to jernplater brukes en stålskrue, som må motstå skjærekrefter på opptil 3200 N. Hva er minimumsdiameteren på skruen hvis sikkerhetsfaktoren er 6.0? Det er kjent at materialet motstår opptil 170 x 10⁶ N/m².

Kan tjene deg: hvit dverg

Løsning

Den skjæreinnsatsen som skruen er utsatt for kommer fra kreftene vist på figuren nedenfor. Sikkerhetsfaktoren er en dimensjonsløs mengde og er relatert til den maksimale tillatte innsatsen:

Kutteinnsats = f/a = maksimal tillatt innsats/sikkerhetsfaktor

Derfor er området:

A = f x sikkerhetsfaktor / skjæreinnsats = 3200 x 6/170 x 10⁶ = 0.000113 m²

Skrueområdet er gitt av πd²/4, derfor er diameteren:

D²= 4 x a/π = 0.000144 moh²

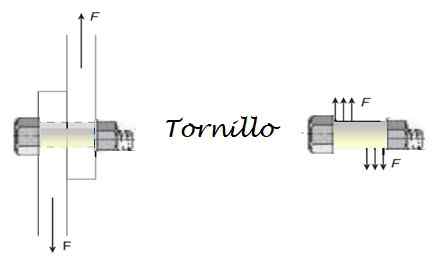Figur 4. Kutte innsatsen på skruen. Kilde: Selvlaget.

D = 0.012 m = 12 mm.

-Oppgave 2

En trepinne eller taco brukes til å forhindre remskiven utsatt for spenninger T₁ og T₂, Angående en 3 -tommers akse. Pin -dimensjonene vises på figuren. Finn størrelsen på skjærspenningen på tacoen, hvis kreftene som er vist på remskiven:

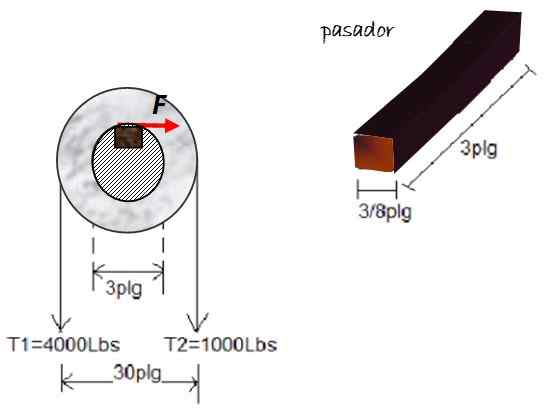Figur 5. Gratis kroppsdiagram for eksempel 2. Kilde: Selvlaget.

Løsning

T₁ produserer et dreiemoment i antihorarium forstand på remskiven, som er tildelt positivt tegn, mens T₂ Produserer dreiemoment i en plan med et negativt tegn. 15 -tommers spakarm for hver spenning. Derfor:

Netto dreiemoment = 4000 pund kraft . 15 tommer - 1000 pund - Force. 15 tommer = 45000 pund-kraft . tomme

Tacoen skal ikke snu, da må øyeblikkene med hensyn til sentrum av tacoen være null. F representerer den gjennomsnittlige kraften på overflaten:

Fire fem.000 - f.D = 0

Med D = 1.5 tommer, derfor:

F x 1.5 = 45.000

F = 30.000 pund

Denne styrken forårsaker en skarp størrelsesorden:

τ = f/a = 30.000 pund-fuerza / (3/8 x 3) tomme² = 2.67 x 10⁴ Libras-Fuerza/Inchga²

Referanser

1. Øl, f. 2010. Materialmekanikk. 5. plass. Utgave. McGraw Hill. 7 - 9.
2. Fitzgerald, 1996. Materialmekanikk. Alpha Omega. 21-23.
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6^th  Ed. Prentice Hall. 238-242.
4. Hibbeler, R.C. 2006. Materialmekanikk. 6. Utgave. Pearson Education. 22 -25
5. Valera Negrete, J. 2005. Generelle fysikknotater. Unam. 87-98.
6. Wikipedia. Skjærspenning. Gjenopprettet fra: i.Wikipedia.org.