Evaluering av funksjoner

For å evaluere en funksjon som diagrammet er kjent, for en viss verdi eller element i startsettet, er det nok å observere det tilsvarende elementet i ankomstsettet. Kilde: f. Zapata.

Hva er evaluering av funksjoner?

De Evaluering av funksjoner Den består i å bestemme bildet av en viss domeneverdi. Med andre ord, for en gitt verdi av startsettet, må du finne det tilsvarende i ankomstsettet.

En funksjon kan være representert på flere måter. Hvis for eksempel Venn -diagrammet er tilgjengelig, er evalueringen veldig enkel, det er nok å velge elementet i start- eller domenesettet, og se elementet som tilsvarer ankomstsettet.

I “…… er kapitaldiagram…”, representert ovenfor, når du evaluerer denne funksjonen i “Canada” -elementet, er det “Ottawa” -elementet, i tilfelle å gjøre det med “Mexico”, er det “Mexico City” og Så videre.

Hvis funksjonen er gitt i form av ryddige par, er evalueringen også enkel: det andre medlemmet av det ordnede dreiemomentet er bildet av det første medlemmet. For eksempel med funksjonen f (x) beskrevet av:

f (x) = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Ved evaluering av funksjonen for verdi 3, er resultatet 6; Når du evaluerer for 5, er det 10 og så videre.

På samme måte kan en funksjon evalueres når grafen er tilgjengelig, forutsatt at verdien du vil evaluere vises i den.

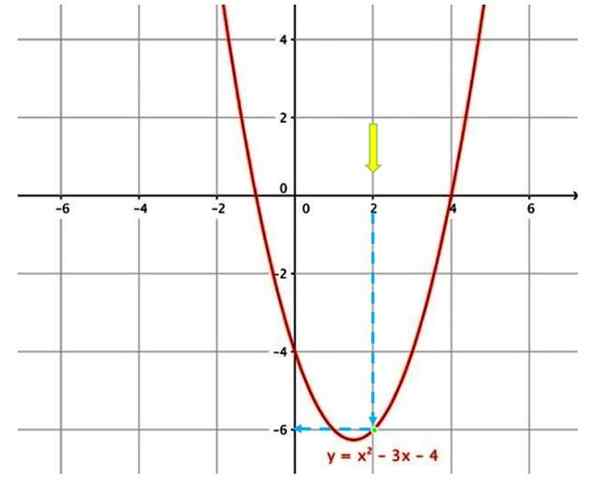Graf for å evaluere en funksjon

For å evaluere funksjonen vist ovenfor, ved x = 2, er for eksempel å finne i graf a x = 2 (gul pil).

Deretter må du bevege deg etter den blå vertikale pilen, til du berører kurven (grønt punkt). Følg den blå pilen igjen, som indikerer den tilsvarende verdien på den vertikale aksen, når du evaluerer funksjonen ved x = 2, oppnås y = −6.

Det kan tjene deg: trigonometriske funksjoner: grunnleggende, i det kartesiske planet, eksempler, trening

Evaluere en gitt funksjon i matematisk notasjon

I den nedre delen av grafen over vises den grafiske funksjonen, men gitt i matematisk notasjon, det vil si gjennom en formel:

f (x) = x² - 3x - 4

Når du vil evaluere funksjonen i hvilken som helst verdi x = a, må du finne f (a), som ganske enkelt leses "f of a".

For å finne resultatet erstattes x = a i funksjonsformelen, og de forespurte operasjonene og beregningene blir utført der.

Anta at du vil evaluere funksjonen til eksemplet på x = −1. Dette betyr at F (−1) må finnes.

Det første trinnet er å erstatte x = -1 i funksjonen:

f (−1) = (−1)² - 3 ∙ (−1) - 4

Og deretter utføre de indikerte operasjonene, som i dette eksemplet er:

• Finn kvadratet med −1: (−1)² = 1
• Trekk den forrige verdien av produkt 3 ∙ (−1): 3 ∙ (−1) = −3
• Fra forrige resultat, trekke fra 4

f (−1) = (−1)² - 3 ∙ (−1) - 4 = 1 + 3 - 4 = 0

Leseren kan bekrefte dette resultatet, fra grafen til funksjonen.

Den beskrevne prosedyren kan brukes til å evaluere funksjonen til en hvilken som helst annen domeneverdi. For eksempel kan du finne F (-2), F (100) eller til og med F (H), der H er en vilkårlig variabel verdi, som tilhører funksjonens domene.

Evaluere en funksjon til en verdi x = h 

Anta at du vil evaluere funksjonen til en eller annen vilkårlig verdi, en hyppig operasjon i matematisk beregning.

I dette tilfellet erstattes X av H, på samme måte som gjøres når X tar noen numerisk verdi, og resultatet blir forenklet så mye som mulig.

Når den resulterende operasjonen ikke lenger kan forenkles, er den resulterende operasjonen igjen.

Det kan tjene deg: enegon: egenskaper, hvordan lage en enegon, eksempler

Eksempel

Du vil evaluere funksjonen f (x) = x² - 3x - 4 ved x = h+1. Den nødvendige tilnærmingen er som følger:

f (h+1) = (h+1)² - 3 ∙ (H+1) - 4

Til rettighetsretten er den første begrepet et bemerkelsesverdig produkt:

(H+1)² = h² +2H + 1

Følgende begrep blir løst gjennom distribusjonseiendom:

3 ∙ (H + 1) = 3H + 3

Når du bytter ut alt det ovennevnte, har du:

f (h+1) = (h+1)² - 3 ∙ (H+1) - 4 = H² +2H + 1 - (3H + 3) - 4

De lignende begrepene reduseres, med algebraisk sum:

f (h+1) = h² + 2H + 1 - 3H - 3 - 4 = H² - H - 6

Differensialskvotienten

Differensialskvotienten eller forholdet mellom forskjeller d for en funksjon f (x) er definert som:

Med tilstand h ≠ 0, som er nødvendig, siden divisjonen med 0 ikke er definert.

Denne kvotienten tolkes geometrisk som skråningen av en sekantlinje til kurven, det vil si en linje som passerer gjennom to punkter av den. Koordinatene for disse punktene er: [x, f (x)] og [x+h; f (x+h)], som sett i følgende figur:

Differensialskvotienten tilsvarer å beregne hellingen på sikringslinjen til kurven, som passerer gjennom punktene som er angitt. Kilde: Wikimedia Commons.

Det er grunnen til at denne kvotienten vises i beregningen av derivatet av en funksjon, siden det å gjøre "h" nærme seg verdien 0, har sekantlinjen en tendens til å bli en tangent linje på punktet (x, y), fordi punktene i skjæringspunktet mellom figuren er så nær at de har en tendens til samme punkt.

Dermed blir linjen tangent (avskjærer kurven i et enkelt punkt).

Dette er nettopp definisjonen av avledet fra en funksjon: skråningen på linjetangenten til kurven i koordinatpunkt (x, f (x))).

Det kan tjene deg: Vektede medier: Hvordan det beregnes, eksempler og øvelser

Som det kan sees, krever differensialkvotienten å evaluere funksjonen i (x + h) og i x. Følgende eksempler illustrerer hvordan du gjør det.

Eksempel 1

Du vil finne den differensielle kvotienten til funksjonen f (x) = 2x - 3. Det første trinnet er å øke evalueringen av funksjonen for x = x + h, som dette:

f (x+h) = 2 ∙ (x+h) - 3 = 2x+2h - 3

Deretter erstattes resultatet i definisjonen av D, gitt tidligere:

Med H ≠ 0.

Telleren er forenklet så langt som mulig, og reduserer lignende vilkår:

Til slutt er de vanlige faktorene i teller og nevner forenklet:

D = 2

Eksempel 2

Finn den differensielle kvotienten til funksjonen f (x) = x² - 3x - 4.

Vi fortsetter som i forrige eksempel, å finne First F (x+h), erstatte resultatet i D og forenkle maksimalt:

f (x+h) = (x+h)² - 3 (x+h) - 4 = x² + 2HX + H² - 3x - 3H - 4

= 2x+H-3

Derfor:

D = 2x+h-3

Hvor h ≠ 0.

Løste øvelser

Oppgave 1

Evaluere funksjonen f (x) = 2x² - 4x + 1 når:

a) x = -1
b) x = 0
c) x = 2

Løsning på

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Løsning b

f (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Løsning c

f (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8 - 8 + 1 = 1

Oppgave 2

Et naturvernsteam bestemte at funksjonen w (t) = 0.Lt² + 1.8t tjener til å modellere mengden avfall "w", i kilo, som kastes i en viss elv, i en tid "t", gitt i dager.

Beregn mengden avfall som kastes i elven i slutten av:

a) 3 dager
b) 1 uke
c) 1 måned

Løsning på

W (t) funksjon evalueres ved t = 3 dager:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kilo

Løsning b

Før du evaluerer, må du bruke 1 uke til dager:

1 uke = 7 dager

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kilo

Løsning c

Igjen er det nødvendig å transformere månedene til dager:

1 måned = 30 dager

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kilo

Referanser

1. Larson, r. 2012. Forkalkning. 8. Utgave. Cengage Learning.
2. Monterey Institute. Evaluering av funksjoner. Gjenopprettet fra: MontereyInstitute.org.
3. Stewart, J. 2007. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
4. Sullivan, m. 1997. Forkalkning. 4. plass. Utgave. Pearson Education.
5. Zill, d. 2008. Preccculment med fremskritt av beregning. 4. plass. Utgave. McGraw Hill.