Vanlige faktoregenskaper, eksempler, øvelser

Han fellesfaktor av et algebraisk uttrykk er en mengde som er til stede i alle vilkår av dette. Når den vanlige faktoren er kjent, er det mulig å skrive uttrykket på en tilsvarende måte gjennom et produkt av faktorer.

Ikke alle algebraiske uttrykk har en felles faktor, det er bare de som bare kan deles mellom dem og 1, derfor er det ikke mulig å skrive dem som et produkt av faktorer. Et eksempel på uttrykk som ikke har noen felles faktor er:

x + y

Figur 1. Den vanlige faktoren til et algebraisk uttrykk gjør det til det indikerte produktet av to faktorer. Kilde: Pixabay.

I stedet dette ja:

5a + 10b

Man ser at de 5 er til stede i begge termer, siden 10 = 5 ∙ 2. Siden 5 er den vanlige faktoren, kan følgende skrives:

5a + 10b = 5 ∙ (a + 2b)

Leseren kan sjekke gjennom distribusjonseiendom, at uttrykket til høyre er lik originalen.

Den vanlige faktoren kan også være bokstavelig eller en kombinasjon av tall og bokstaver, for eksempel i 4x² - 2x. De x og 2 De er mellom faktorene og uttrykket forblir som et produkt:

4x² -2x = 2x⋅ (x -1)

Fordelen med å finne den vanlige faktoren for et uttrykk og skrive det som et produkt er at det nesten alltid er lett å operere med det. Derfor brukes det i mange algebraiske og beregningsprosedyrer som:

-Når du løser ligninger, hvis løsninger raskt blir avslørt når den vanlige faktoren blir funnet.

-Når du beregner en grense med en ubestemmelse, kan dette forsvinne ved å faktorere ordentlig.

-Den passende faktoriseringen letter også operasjoner med rasjonelle algebraiske uttrykk, for eksempel summer og subtraksjoner.

[TOC]

Vanlige faktoregenskaper

Hovedegenskapene til den vanlige faktoren er som følger:

-Det kan være et tall, et algebraisk uttrykk eller en kombinasjon av begge deler.

-Den vanlige faktoren må være inneholdt i hvert av vilkårene for uttrykket for å faktor.

Kan tjene deg: Transcendente funksjoner: Typer, definisjon, egenskaper, eksempler

-I henhold til mengden vilkår det inneholder, kan det være tilfelle av:

1. Vanlig monomial faktor, hvis den vanlige faktoren er av et enkelt begrep,
2. Vanlig binomial faktor hvis du har to begreper og
3. Vanlig polynomfaktor, hvis den vanlige faktoren består av flere begreper.

Hvordan finne den vanlige faktoren til et algebraisk uttrykk?

For å finne den vanlige faktoren som er til stede i et polynom, må du beregne den maksimale vanlige divisoren eller MCD for de numeriske koeffisientene for alle begrepene, samt bokstavene eller litteralene i hvert begrep og velg kraften med den minste eksponent.

Brevene eller litteraturene kan presenteres som monomialer, binomials eller polynomer, som det vil bli sett i følgende eksempler.

Den mest anbefalte å forstå prosessen med å oppnå den vanlige faktoren, er å følge eksemplene og øve på å løse flere øvelser i hvert tilfelle.

Vanlige faktoreksempler

Vi må ikke miste synet av det faktum at målet med felles faktor blir konvertert et uttrykk til et indikert produkt av faktorer. Da blir de mest relevante sakene analysert:

Vanlig monomial faktor

Du har følgende monomialer (enkelt -term algebraiske uttrykk):

2x²; 10x⁴og; 100x⁶og²

Hva kan være den vanlige faktoren for de tre?

Fra og med de numeriske koeffisientene: 2, 10 og 100, alle er jevn og deres MCD er 2. Når det gjelder den bokstavelige delen, er variabel x til stede i de tre begrepene, og den laveste strømmen er x², Da er den vanlige faktoren 2x².

De tre foreslåtte vilkårene kan skrives som produkter av denne faktoren på denne måten:

2x²= 2x²∙ 1

10x⁴y = 2x² ∙ 5x²og

100x⁶og²= 2x²∙ 50x⁴og²

Multipliserer faktorene til høyre, kan det bekreftes at venstresiden er oppnådd.

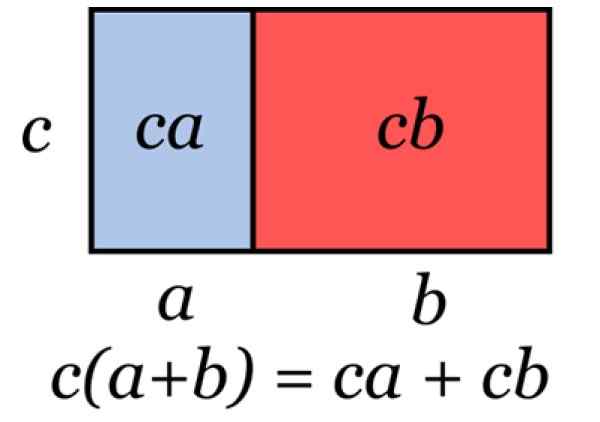Figur 2. Illustrasjon som representerer den vanlige faktoren. Kilde: Wikimedia Commons.

Denne teknikken brukes når den er nødvendig for å faktorere et algebraisk uttrykk, som i følgende eksempler:

• Eksempel 1

Faktum følgende uttrykk:

Det kan tjene deg: Isosceles Triangle

5x³og + 10x²og² + 5xy²

MCD for de numeriske koeffisientene for hvert begrep er:

MCD (5.10) = 5

Når det gjelder den bokstavelige delen, begge x som og De er til stede i de tre begrepene, og minst eksponenten for hver er 1, derfor er den vanlige faktoren 5xy Og du kan skrive:

5x³og + 10x²og² + 5xy²= 5xy ∙ (x² +2xy²+og)

Vanlig polynomfaktor

Den vanlige faktoren kan bestå av en binomial, en trinomial eller generelt i et polynomial. I dette tilfellet er instruksjonene i forrige seksjon fortsatt gyldige, og velger som en vanlig faktor den med den minste eksponenten.

• Eksempel 2

Skriv følgende uttrykk som produkt av to faktorer:

2a (x - 1) - 3b (x - 1)

Ved direkte inspeksjon er den vanlige faktoren binomial (X-1), så:

2a (x - 1) - 3b (x - 1) = (x -1) ∙ (2a - 3b)

Faktorisering ved å gruppere vilkår

Noen ganger er eksistensen av en vanlig faktor ikke tydelig, men det avsløres hvis begrepene er gruppert på en praktisk måte:

• Eksempel 3

Faktoriser 3x³ - 9ax² - x + 3a

Ved første øyekast er det ingen felles faktor i disse fire begrepene, siden for eksempel x Det er til stede i de tre første, men ikke i det siste. Og til Det er i den andre og i den siste ikke noe mer.

Når det gjelder koeffisientene, er det tre begreper der de 3 er til stede, men for å være en vanlig faktor, bør det være i alle termer.

Det ser ut til at de beskrevne teknikkene ikke kan brukes denne gangen. Imidlertid kan uttrykket være å ta faktorering ved å gruppere de to første begrepene og de to siste, og være forsiktige når du plasserer parentesen, at tegnene er passende for ikke å endre originalen:

Kan tjene deg: rektangulære komponenter i en vektor (med øvelser)

3x³ - 9ax² - x + 3a = (3x³ - 9ax²) - (x - 3a)

Legg merke til det negative tegnet midt i parenteser: det er nødvendig, for ellers vil det opprinnelige uttrykket endres.

I venstre parentes er den vanlige faktoren 3x², derfor:

(3x³ - 9ax²) - (x - 3a) = 3x²⋅ (x - 3a) - (x - 3a)

Og det observeres at en vanlig faktor allerede har dukket opp: (x - 3a), Det vil si at det er faktor for andre gang å oppnå:

3x² (x- 3a) - (x - 3a) = (x - 3a) ∙ ( 3x²- 1)

Vanlige faktorøvelser

Oppgave 1

Løs 4x -ligningen³ +7x²  +6x = 0

Løsning

"X" er en vanlig faktor, derfor:

3x³ −5x²  +2x = x (3x² −5x +2) = 0

For uttrykket til venstre er det 0, det er nok at en av disse to forholdene er oppfylt:

x = 0

ENTEN:

3x² −5x +2 = 0

Dette er en komplett andre grads ligning som kan løses ved å bruke den generelle formelen, også ved å bruke en vitenskapelig kalkulator eller annen algebraisk metode. Løsningene av denne ligningen er:

x = 1

x = 2/3

Når det er funnet, er det illustrerende å skrive ligningen som et produkt av 3 faktorer, selv om uttalelsen ikke ba om det. Det ville være slik:

x⋅ (x-1) ⋅ (x-2/3) = 0

Oppgave 2

Beregn følgende grense hvis den eksisterer:

Løsning

Først erstattes den ved x = −2 for å prøve å evaluere grensen, ved å gjøre det oppnås:

Ettersom det er en ubestemmelse av 0/0 -skjemaet, må du være faktor for å prøve å eliminere den. Denominatoren kan ikke være faktor, men telleren gjør det.

I telleren er den vanlige faktoren x:

x²+2x = x ∙ (x+2)

Det faktoriserte uttrykket erstattes i grensen, og på denne måten forsvinner ubestemmelsen:

Det konkluderes med at grensen eksisterer og er verdt −2.

Referanser

1. Baldor, a. 2005. Algebra. Kulturell hjemlandsgruppe.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Larson, r. 2012. Forkalkning. 8. Utgave. Cengage Learning.
4. Stewart, J. 2007. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.