Volumetrisk flyt

Vi forklarer hva volumetrisk flyt er, hvordan du beregner den og faktorene som påvirker den

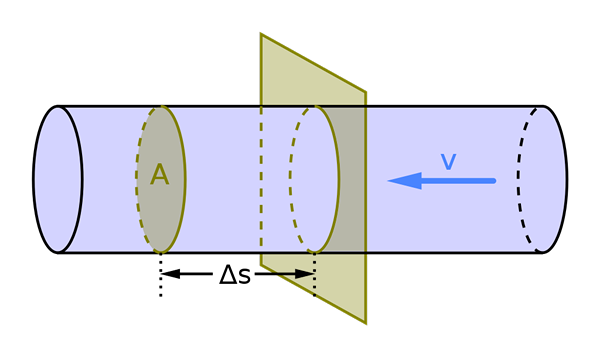
Den volumetriske strømmen avhenger av området i tverrsnitt A og hastigheten på væske V. Kilde: Mikerun, CC BY-SA 4.0, via Wikimedia Commons

Hva er volumetrisk flyt?

Han Volumetrisk flyt Det gjør det mulig å bestemme volumet av væske som krysser en del av kanalen og gir et hastighetsmål som væsken beveger seg med det samme. Derfor er tiltaket spesielt interessant på områder som er så forskjellige som industri, medisin, konstruksjon og forskning, blant andre.

Å måle hastigheten på en væske (enten en væske, en gass eller en blanding av begge) er imidlertid ikke så enkel som forskyvningshastigheten til en solid kropp kan være å måle. Derfor hender det at for å vite hastigheten på en væske er det nødvendig å vite strømmen.

Fra dette og mange andre problemer relatert til væsker, avgir grenen av fysikk kjent som Fluid Mechanics. Strømmen er definert som hvor flytende en del av en kanal går gjennom, den er allerede en rørledning, en rørledning, en elv, en kanal, en blodomløp, etc., ta hensyn til en midlertidig enhet.

Vanligvis beregnes volumet som et bestemt område i en tidsenhet beregnet, også kalt volumetrisk strømning. Masse- eller massestrømmen som krysser et område som er bestemt på et bestemt tidspunkt, er også definert, selv om det brukes sjeldnere enn volumetrisk strømning.

Hvordan beregnes volumetrisk strømning?

Den volumetriske strømmen er representert med bokstaven q. For tilfeller der strømmen beveger seg vinkelrett på førerseksjonen, bestemmes den med følgende formel:

Q = a = v / t

I denne formelen A er det førerseksjonen (det er gjennomsnittshastigheten som væsken har), V er volumet og T -tiden. Siden i det internasjonale systemet måles området eller delen av sjåføren i m² Og hastigheten i m/s, strømmen måles m³/s.

Kan tjene deg: 21 viktige hendelser i fysikk

For tilfeller der hastigheten på væskeforskyvning skaper en vinkel θ med retningen vinkelrett på overflateseksjonen A, er uttrykket for å bestemme strømmen som følger:

Q = a cos θ

Dette er i samsvar med den forrige ligningen, siden når strømmen er vinkelrett på område a, θ = 0 og derfor cos θ = 1.

Ovennevnte ligninger er bare sanne hvis væskehastigheten er ensartet, og hvis delen av seksjonen er flat. Ellers beregnes den volumetriske strømmen gjennom følgende integral:

Q = ∫∫_s V D s

I denne integrerte DS er det overflatevektoren, bestemt av følgende uttrykk:

Ds = n ds

Der er N den normale enhetsvektoren til overflaten av kanalen og DS et differensialoverflateelement.

Kontinuitetsligning

Et kjennetegn ved inkomprimerbare væsker er at væskemassen er bevart ved hjelp av to seksjoner. Dette er grunnen til at kontinuitetsligningen er oppfylt, som etablerer følgende forhold:

ρ₁ TIL₁ V₁ = ρ₂ TIL₂ V₂

I denne ligningen ρ er væskens tetthet.

For tilfeller av regimer i permanent strømning, der tettheten er konstant og derfor er det oppfylt at ρ₁ = ρ₂, Det reduseres til følgende uttrykk:

TIL₁ V₁ = A₂ V₂

Dette tilsvarer å bekrefte at strømmen er bevart og derfor:

Q₁ = Q₂.

Fra observasjonen av ovennevnte følger det at væskene akselererer når de når en smalere del av en kanal, mens de reduserer hastigheten når de når en bredere del av en kanal. Dette faktum har interessante praktiske anvendelser, siden det tillater å leke med hastigheten på forskyvning av en væske.

Kan tjene deg: subatomiske partikler

Bernoulli -prinsippet

Bernoulli -prinsippet bestemmer at for en ideell væske (det vil si en væske som verken har viskositet eller friksjon) som beveger seg i et sirkulasjonsregime gjennom en lukket kanal blir oppfylt at energien forblir konstant gjennom hele forskyvningen.

Til syvende og sist er Bernoulli -prinsippet ingenting annet enn formuleringen av energibesparelsesloven for strømmen av en væske. Dermed kan Bernoulli -ligningen formuleres som følger:

H +V² / 2g+p/ ρg = konstant

I denne ligningen h er høyden og G er akselerasjonen av tyngdekraften.

I Bernoulli -ligningen tas energien til en væske når som helst, energi bestående av tre komponenter.

• En kinetisk komponent som inkluderer energi, på grunn av hastigheten som væsken beveger seg.
• En komponent generert av gravitasjonspotensialet, som en konsekvens av høyden som væsken er lokalisert.
• En komponent av strømningsenergi, som er energien som en væske har på grunn av trykket.

I dette tilfellet uttrykkes Bernoulli -ligningen som følger:

H ρ g +(v² ρ)/2 + p = konstant

Logisk sett, i tilfelle av en reell væske, blir ikke uttrykket av Bernoulli -ligningen oppfylt, siden det i forskyvningen av væsken er friksjonstap og det er nødvendig å ty en mer kompleks ligning.

Hva som påvirker volumetrisk strømning?

Den volumetriske strømmen vil bli påvirket hvis det er en hindring i kanalen.

Kan tjene deg: Lett refraksjon: elementer, lover og eksperiment

I tillegg kan den volumetriske strømmen også endres etter virkning av temperatur- og trykkvariasjonstemperatur og trykket som den er.

Enkel metode for å måle volumetrisk strømning

En virkelig enkel metode for å måle den volumetriske strømmen er å la en væskestrøm i en måletank i en viss periode.

Denne metoden er generelt ikke veldig praktisk, men sannheten er at den er ekstremt enkel og veldig illustrerende å forstå betydningen og viktigheten av å kjenne strømmen av en væske.

På denne måten får væsken lov til å strømme inn i en måletank i en periode, det akkumulerte volumet måles og resultatet oppnådd mellom den forløpte tiden er delt.

Referanser

1. Flyt (væske) (n.d.).  I Wikipedia. Gjenopprettet fra Es.Wikipedia.org.
2. Volumetrisk strømningshastighet (n.d.).  I Wikipedia. Innhentet fra.Wikipedia.org.
3. Engineers Edge, LLC. "Fluid Volumetric Flow Rate Equation". Kantingeniører
4. Mott, Robert (1996). "1". Anvendt væskemekanikk (4. utgave). Mexico: Pearson Education.
5. Batchelor, g.K. (1967). En introduksjon til flytende dynamikk. Cambridge University Press.
6. Landau, l.D.; Lifshitz, e.M. (1987). Væskemekanikk. Forløp av teoretisk fysikk (2. utgave.). Pergamon Press.