Dynamisk eller kinetisk friksjonskoeffisient, eksempler, øvelser

De Dynamisk friksjon eller kinetisk Det er den som oppstår mellom to kropper i kontakt når overflaten til den ene av dem beveger seg med hensyn til overflaten til den andre. For eksempel i en boks som glir friksjonen i en skråning er dynamisk og distribuert på kontaktflaten på blokken.

Helling må være stor nok, slik at den tangensielle komponenten i vekten tilsvarer eller overvinner friksjonskraften, ellers vil blokken som stiger ende opp med å stoppe.

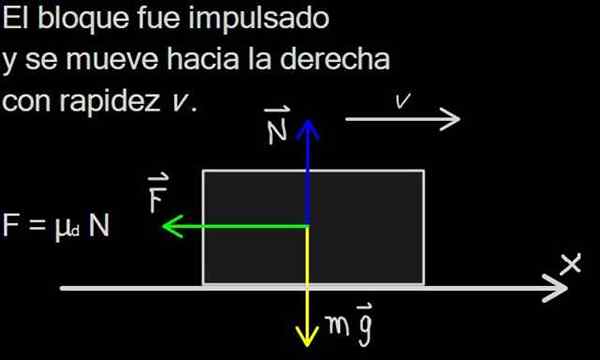
Figur 1. Friksjonskraften er distribuert på kontaktflaten til blokken, men i kreftene er det representert som en enkelt kraft F, kilde: f. Zapata

Friksjonskraften er av ekstrem betydning i dagliglivet, siden den tillater bevegelse av mennesker, dyr og kjøretøy. På en friksjonsfri overflate, for eksempel en iskrem, er det ikke mulig å starte bevegelsen.

Friksjon lar også bilene våre stoppe når de beveger seg.

Når du bruker bremsene, strammes bremseklossene mot hjulskiver og takket være dynamisk friksjon, stopp rotasjonen av dem. Men det er ikke nok å ha gode bremser, det er nødvendig at det er nok friksjonsstyrke mellom dekkene og gulvet, for endelig er dette kraften vi er avhengige av slik at bilen stopper.

Menneskeheten har lært å håndtere friksjon til fordel for fordelen. Dermed begynte med å bruke friksjon mellom to stykker tørt tre for å lage ild.

Naturen har også lært å håndtere friksjon i sin favør. For eksempel er synoviale membraner som dekker beinene i leddene en av overflatene med den laveste friksjonskoeffisienten som finnes.

[TOC]

Dynamisk friksjonskoeffisient

Den første som systematisk studerte bevegelsen av en blokk som glir på en flat overflate, var Leonardo da Vinci, men studiene hans gikk upåaktet hen.

Kan tjene deg: Dirac Jordan Atomic Model: Egenskaper og postulater

Det var først på det syttende århundre at den franske fysikeren Guillaume Amontons gjenoppdaget friksjonslovene:

Dynamiske friksjonslover

1.- Friksjonskraften som er til stede i en blokk som glir på en flat overflate, motsetter seg alltid bevegelsesretningen.

2.- Størrelsen på den dynamiske friksjonskraften er proporsjonal med den normale tettheten eller kraften mellom blokkenes overflater og støtteplanet.

3.- Den proporsjonale konstanten er friksjonskoeffisienten, statisk μ_og I tilfelle å ikke ha glid og dynamisk μ_d Når det er. Friksjonskoeffisienten avhenger av materialene på overflatene i kontakt og grovhetstilstand.

4.- Friksjonskraften er uavhengig av det tilsynelatende kontaktområdet.

5.- Når bevegelsen av den ene overflaten begynner med hensyn til den andre, er friksjonskraften konstant og avhenger ikke av den relative hastigheten mellom overflatene.

I tilfelle er det ingen glidning, statisk friksjon brukes hvis kraft er mindre enn eller lik den statiske friksjonskoeffisienten multiplisert med normal.

Figur 2. Den dynamiske friksjonskraften motsetter seg bevegelsesretningen og dens størrelse er proporsjonal med normalkraft. Proporsjonalitetskonstanten er den dynamiske friksjonskoeffisienten. Kilde: f. Zapata.

Den siste eiendommen var resultatet av bidraget fra den franske fysikeren Charles Augustin fra Coulomb, bedre kjent for sin berømte styrkelov mellom spesifikke elektriske anklager.

Disse observasjonene fører oss til den matematiske modellen for dynamisk friksjonskraft F:

F = μ_d N

Hvor μ_d Det er den dynamiske friksjonskoeffisienten og N er normalkraften.

Hvordan bestemme den dynamiske friksjonskoeffisienten?

Den dynamiske friksjonskoeffisienten mellom to overflater bestemmes eksperimentelt. Verdien avhenger ikke bare av materialene på begge overflater, men av grovhet eller polering som de har, så vel som dens renslighet.

Kan tjene deg: Mekaniske bølger: Kjennetegn, egenskaper, formler, typer

En måte å bestemme det på er å øke og skyve en kjent boks på en horisontal overflate.

Hvis hastigheten er kjent på tidspunktet for å bli kjørt og avstanden fra den tiden måles, er det mulig å kjenne bremseakselerasjonen på grunn av dynamisk friksjon.

Eksperiment 

I dette eksperimentet måles den opprinnelige hastigheten v og avstanden d, Så bremseakselerasjonen er:

A = - v² / 2d

Krefter -diagrammet er vist i figur 2. Vektens størrelse er massen m av blokken multiplisert med akselerasjonen av tyngdekraften g, og som kjent peker vekten alltid vertikalt ned.

N Det er normalkraften på grunn av skyvet opp støtteoverflaten og er alltid vinkelrett (eller normal) til flyet. Normal eksisterer mens overflatene er i kontakt og opphører så snart overflatene er atskilt.

Kraften F representerer den dynamiske friksjonskraften. Den er faktisk distribuert på den nedre overflaten av blokken, men vi kan representere den som en enkelt kraft F brukt i midten av blokken.

Ettersom det er vertikal balanse, størrelsen på det normale N Det er lik den for vekten Mg:

N = mg

I horisontal retning produserer friksjonskraften retardasjonen av masseblokken M i henhold til Newtons andre lov:

-F = m a

Friksjonskraften F peker til venstre, så den horisontale komponenten er negativ, M er massen av blokken og A er bremseakselerasjonen.

Hadde tidligere oppnådd A = - v² / 2d Og også den dynamiske friksjonsmodellen indikerer at:

F = μd n

Erstatte i forrige ligning du har:

-μ_d N = - v² / 2d

Når du tar hensyn til at n = mg, kan du allerede fjerne den dynamiske friksjonskoeffisienten: 

Kan tjene deg: Schrödinger atommodell

μ_d = v² / (2d MG)

Rocy koeffisientbord av noen materialer

Følgende tabell viser de statiske og dynamiske friksjonskoeffisientene for forskjellige materialer. Det skal bemerkes at systematisk den statiske friksjonskoeffisienten alltid er større enn den dynamiske friksjonskoeffisienten.

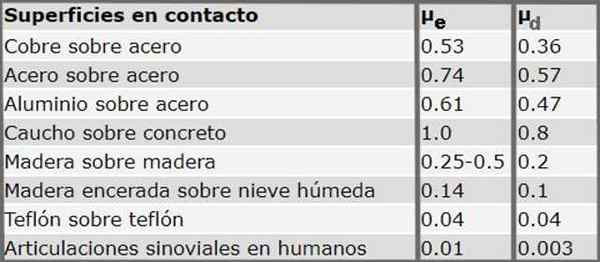Figur 3. Statiske og dynamiske friksjonskoeffisienter for flere overflater i kontakt. Kilde: Serway R.TIL. Fysisk. McGraw-Hill (1992)

Øvelser

- Oppgave 1

En 2 kg blokk med deig på et horisontalt gulv fremmes og den frigjøres. På tidspunktet for å bli utgitt blir en hastighet på 1,5 m/s spilt inn. Fra det øyeblikket til blokken er innom dynamisk friksjon 3 m. Bestem den kinetiske friksjonskoeffisienten.

Løsning

I henhold til formelen oppnådd i eksemplet fra forrige seksjon, er det dynamisk (eller kinetisk) koeffisient:

μ_d = v² / (2d mg) = 1.52 / (2x3x2 x9,8) = 0,019.

- Oppgave 2

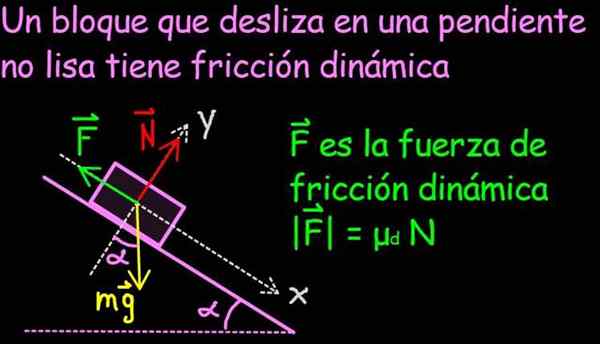
Å vite at blokken i figur 1 går ned med konstant hastighet, at massen på blokken er 1 kg og at hellingen av planet er 30º, bestemmer:

a) Verdien av den dynamiske friksjonen

b) Den dynamiske friksjonskoeffisienten mellom blokken og planet.

Løsning

I figur 4 er bevegelsesligningen (Second Law of Newton) vist for problemet med en blokk som går ned en skråning med friksjonskoeffisient μ_d  og α helling (se krefter diagram i figur 1)

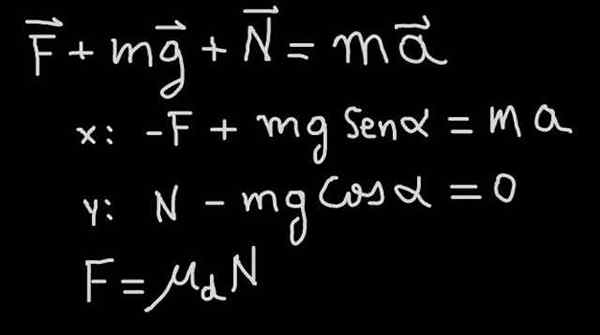Figur 4. Newtons andre lov gjaldt blokken som glir i en skråning med friksjon. Kilde: f. Zapata.

I vår øvelse blir vi fortalt at blokken går ned med konstant hastighet, derfor går ned med akselerasjon a = 0. Derfra følger det at friksjonskraften er slik at den tilsvarer den tangensielle komponenten i vekten: f = mg sen (α).

I vårt tilfelle M = 1 kg og α = 30º slik at friksjonskraften F har en verdi på 4,9N.

På den annen side er normalkraften n den samme og i motsetning til den vinkelrett komponenten i vekten: n = mg cos (α) = 8,48n .

Derfra følger det at den dynamiske friksjonskoeffisienten er:

μ_d = F / n = 4,9n / 8,48n = 0,57

Referanser

1. Alonso m., Finn e. 1970. Fysisk. Volum I. Mekanikk. Inter -American Education Fund s.TIL.
2. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
3. Hewitt, p. 2012. Konseptuell fysisk vitenskap. Femte utgave.
4. Rex, a. 2011. Fundamentals of Physics. Pearson. 
5. Serway r. 1992. Fysisk. McGraw-Hill.
6. Young, h. 2015. Universitetsfysikk med moderne fysikk. 14. utg. Pearson.