Generelle formel kvadratiske ligninger, eksempler, øvelser

De Generell formel, som også er kjent som Løsningsmiddelformel I noen tekster brukes den til å løse andre grads ligninger: øks² + BX + C = 0.

I dem til, b og c De er reelle tall, med betingelse av at til er forskjellig fra 0, å være x Det ukjente. Deretter presenterer den generelle formelen klarering av det ukjente gjennom et uttrykk som involverer verdiene til til, b og c følgende:

Figur 1. Den generelle formelen i matematikk brukes til å løse kvadratiske ligninger. Kilde: f. Zapata.

Og gjennom denne formelen kan du finne løsningen av andre grad eller kvadratisk ligning, forutsatt at den nevnte løsningen eksisterer.

I følge historikere var den generelle formelen allerede kjent av den gamle babylonske matematikken. Det ble deretter overført til andre folk, som egypterne og grekere, gjennom kulturelle utvekslinger.

Formelen og dens varianter ankom Europa takket være muslimske matematikere som bosatte seg på den iberiske halvøya. De brukte imidlertid ikke den algebraiske notasjonen som vi bruker for øyeblikket. Denne notasjonen skyldes den franske matematikeren og kryptografisk ekspert fra 1500 -tallet Francois Viete.

[TOC]

Kvadratiske ligninger etter den generelle formelen

La oss se hvordan den generelle formelen oppstår, for å bekrefte gyldigheten. Starter fra en generell kvadratisk ligning:

øks² + BX + C = 0

La oss utføre noen enkle algebraiske manipulasjoner, for å oppnå klarering av det ukjente. Det er flere måter å bære dette på, for eksempel å fullføre firkanter, som vist da.

Demonstrasjon av den generelle formelen

Vi begynner med å legge til (-c) på begge sider av likhet:

øks² + BX = - C

Og nå multipliseres det med 4A, alltid på begge sider av likhet, for ikke å endre uttrykket:

4. plass² x² + 4AB x = - 4AC

Legge til b²:

4. plass²⋅x² + 4Ab⋅x + b² = - 4ac + B²

Hensikten med dette er å fullføre firkanter på venstre side av likhet, som inneholder det ukjente, på denne måten blir klarering tilrettelagt. Dermed:

Kan tjene deg: Divisors of 8: Hva er og enkel forklaring

-Første periode: 4² x² Det er det perfekte firkanten av 2ax

-Den siste, som er B², Det er det perfekte firkanten av B.

-Og den sentrale uttrykket er det doble produktet av 2AX og B: 2⋅2ax⋅B = 4ABX

Derfor har vi en firkantet binomial:

4. plass²⋅x² + 4Ab⋅x + b² = (2ax + b)²

Og vi kan skrive:

(2ax + b)² = - 4ac + B²

Vi er et skritt unna å rydde det ukjente x:

Og vi oppnår allerede den generelle formelen vi kjenner:

Det er andre måter å algebraisk manipulere den kvadratiske ligningen og oppnå samme resultat.

Eksempler på bruk av den generelle formelen

For å bruke den generelle formelen, blir verdiene til A, B og C nøye bestemt og erstattet i formelen. Legg merke til symbolet mer mindre i telleren; Dette indikerer at vi må vurdere to muligheter angående operasjonen, en med skiltet + og en med skiltet -.

Den kvadratiske ligningen kan ha følgende løsninger, i henhold til verdien av den subradiske mengden, kjent som diskriminerende:

-Ja b² - 4ac> 0, den kvadratiske ligningen har to virkelige og forskjellige løsninger.

-Når b² - 4ac = 0, har ligningen en unik løsning, gitt av:

x = -b/2a

-Til slutt, hvis B² - 4ac < 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

La oss se på noen eksempler der den generelle formelen brukes, og legger merke til at hvis noen av koeffisientene som følger med det ukjente ikke vises, er det forstått at det er verdt 1. Og hvis det uavhengige uttrykket er den som ikke er funnet, er det verdt 0.

- Eksempel 1

Løs følgende kvadratiske ligninger:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Svar til

Vi skriver koeffisientene for hvert begrep: a = 6, b = 11, c = -10 og erstatter verdiene i den generelle formelen:

Kan tjene deg: beskatning

x = (-11 ± 19) /12

Resultatet fører til følgende to virkelige løsninger:

x₁ = (-11 + 19)/12 = 8/12 = 2/3

x₂ = (-11 -19)/12 = -5/2

Svar b

Igjen bestemmes koeffisientene: a = 3, b = -5 og c = -1. Ved å bytte ut i formelen:

I motsetning til det forrige tilfellet, er kvadratroten av 37 ikke et heltall, men vi kan også heve de to løsningene og etterlate roten eller finne den tilsvarende desimalverdien ved hjelp av kalkulatoren:

x₁ = (-5 + √37)/6 ≈ 0.18

x₂ = (-5 - √37)/6 ≈ - 1.85

- Eksempel 2

Løs andre grads ligning x² - 4x +13 = 0.

Svar

Som alltid identifiserer vi verdiene til koeffisientene og erstatter den generelle formelen: a = 1, b = - 4, c = 13. Dette leder til:

Vi har en negativ rot, derfor er løsningene av denne ligningen komplekse tall. Roten kan uttrykkes i form av Yo, de Imaginær enhet:

√ (36i²) = 6i

Siden jeg² = -1, derfor er de komplekse løsningene:

x₁ = (4 + 6i)/2 = 2 + 3i

x₂ = (4 - 6i)/2 = 2 - 3i

Trening løst

En 10 m lang trapp hviler mot en vertikal vegg, med foten 6 m fra den veggen. Trappen glir og foten er atskilt 3 m mer fra basen.

Finn den vertikale avstanden som går gjennom toppen av trappen.

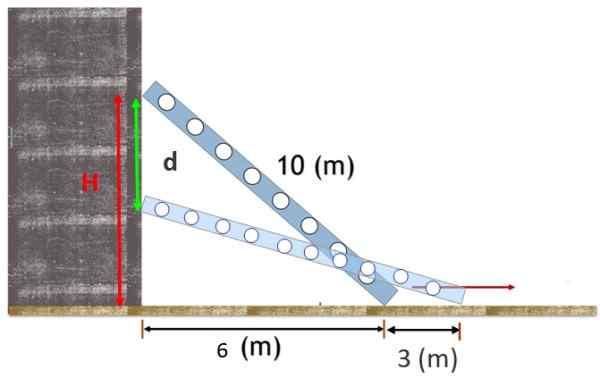Figur 2. En trapp støttet på en vegg glir litt og øvre stopp beveger seg vertikalt ned en avstand d. Kilde: f. Zapata.

Løsning

For å finne den vertikale avstanden som skyver toppen av trappen, må du finne den posisjonen den opprinnelig var angående bakken. Vi kan gjøre det med Pythagoras -teoremet, fordi figuren som er dannet er det av en riktig trekant:

H = (10² - 6²) ^½ = 8 m

Når trappen glir, beveger en avstand d, Mål siden toppen var 8 m høy, til den nådde sin nye stilling, ved (H-D) meter over bakken. Det ukjente å fjerne er D.

Kan tjene deg: Akkumulert frekvens: Formel, beregning, distribusjon, eksempler

For å finne den foreslår vi en ny rektangel -trekant, som dannes etter at stigen gled litt. Denne trekanten har fremdeles hypotenusa lik 10 m og parallellkateto er nå 6m + 3m = 9 m, derfor:

(H-D)² = 10² - 9² = 100 - 81 = 19

Vi erstatter H = 8m, tidligere beregnet:

(8-D)² = 19

Ligningen kan løses på flere måter, inkludert bruk av den generelle formelen, som vi vil vise nedenfor med disse trinnene:

Trinn 1

Utvikle den bemerkelsesverdige venstresiden til venstre:

64 -16d + D² = 19

Steg 2

Etablere den andre gradslikningen for ukjent d:

d² - 16d + 45 = 0

Trinn 3

-Koeffisientene er: a = 1, b = -16 og c = 45, vi erstatter dem i den generelle formelen:

Løsningene av ligningen er:

d₁ = (16 + √76)/2 ≈ 12.36 m

d₂ = (16 - √76)/2 ≈ 3.64 m

Trinn 4

Løsningene som er oppnådd blir analysert: den første gir ikke fysisk mening, siden det ikke er mulig for stigen å kompilere 12.36 m, hvis opprinnelig stoppet var 8 m høy på bakken.

Derfor er riktig svar den andre løsningen: toppen av trappen glir d = 3.64 m.

Kan leseren løse problemet ved å bruke en annen metode?

Referanser

1. Baldor. 1977. Elementær algebra. Venezuelanske kulturutgaver.
2. Hoffman, J. Valg av matematikkproblemer. Volum 2.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.