Konstante karakteristikkfunksjon, eksempler, øvelser

De konstant funksjon Det er en der verdien av og. Med andre ord: en konstant funksjon har alltid skjemaet  f (x) = k, hvor k Det er et reelt tall.

Ved å tegne den konstante funksjonen i koordinatsystemet Xy, Det er alltid en rett linje parallelt med den horisontale aksen eller aksen til x.

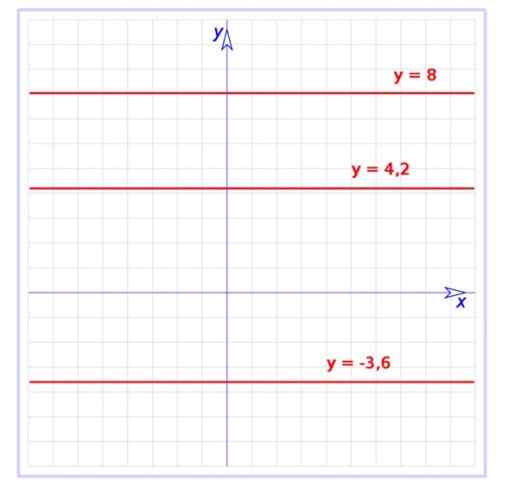
Figur 1. Graf over flere konstante funksjoner på det kartesiske planet. Kilde: Wikimedia Commons. Bruker: Hite [Public Domain]

Denne funksjonen er et spesielt tilfelle av relatert funksjon, hvis graf også er en rett linje, men med skråning. Den konstante funksjonen har en null i påvente, det vil si at den er en horisontal linje, som vist i figur 1.

Det er grafen over tre konstante funksjoner:

f (x) = -3.6

G (x) = 4.2

H (x) = 8

Alle er rett parallelle med den horisontale aksen, den første er under den aksen, mens de resterende er over.

[TOC]

Kjennetegn på den konstante funksjonen

Vi kan oppsummere hovedegenskapene til den konstante funksjonen som følger:

-Grafen er en horisontal rett linje.

-Den har unikt kryss med aksen og, verdi k.

-Det er kontinuerlig.

-Mestring av den konstante funksjonen (settet med verdier som x) er settet med reelle tall R.

-Ruten, rekkevidden eller motsetningen (settet med verdier som variabelen tar og) er ganske enkelt konstanten k.

Eksempler

Funksjonene er nødvendige for å etablere koblinger mellom størrelser som er avhengige av hverandre på noen måte. Det eksisterende forholdet mellom dem kan modelleres matematisk, for å vite hvordan en av dem oppfører seg når den andre varierer.

Kan tjene deg: papomudas

Dette hjelper med å bygge modeller i mange situasjoner og komme med spådommer om deres oppførsel og evolusjon.

Til tross for sin tilsynelatende enkelhet, har den konstante funksjonen mange applikasjoner. For eksempel når det gjelder å studere størrelser som forblir konstante i tid, eller i det minste, for en betydelig tid.

På denne måten oppfører størrelser seg i situasjoner som følgende:

-De hastighet Cruise av en bil som beveger seg på en lang rettlinjet motorvei. Så lenge den ikke stopper eller akselererer, bærer bilen en jevn rettlinjet bevegelse.

Figur 2. Hvis bilen ikke stopper eller akselererer, har den en jevn rettlinjet bevegelse. Kilde: Pixabay.

-En fullastet og frakoblet kondensator fra en krets, har en byrde konstant i tid.

-Til slutt opprettholder en parkering med fast rente, en pris konstant uansett hvor lang bil parkert der.

En annen måte å representere en konstant funksjon

Den konstante funksjonen vekselvis kan representeres som følger:

f (x) = kx⁰

Siden enhver verdi av x hevet til 0 gir 1 som et resultat, er det forrige uttrykket redusert til det kjente:

f (x) = k

Selvfølgelig skjer det så lenge verdien av k er forskjellig fra 0.

Det er grunnen til at den konstante funksjonen også er klassifisert som en Polynomfunksjon Grad 0, siden eksponenten for variabelen x Det er 0.

Løste øvelser

- Oppgave 1

Svar på følgende spørsmål:

a) Kan det bekreftes at linjen gitt av x = 4 er en konstant funksjon? Årsak til svaret ditt.

b) Kan en konstant funksjon ha kryss med x -aksen?

c) er funksjonen f (x) = w konstant²?

Svar til

Her er grafen til linjen x = 4:

Kan tjene deg: statistiske variabler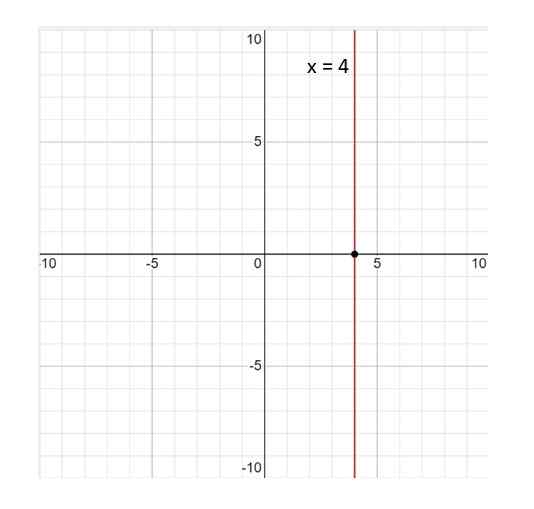 Figur 3. Graf over linjen x = 4. Kilde: f. Zapata.

Linjen X = 4 er ikke en funksjon; Per definisjon er en funksjon et forhold slik at til hver verdi av variabelen x Det tilsvarer en enkelt verdi av og. Og i dette tilfellet er dette ikke oppfylt, siden verdien x = 4 er assosiert med uendelige verdier av og. Derfor er svaret nei.

Svar b

Generelt har en konstant funksjon ikke noe kryss med aksen x, Med mindre det er det y = 0, I så fall er det aksen x Ordentlig sagt.

Svar c

Ja, siden W Det er konstant, det er også torget. Hva interesser er at W Det avhenger ikke av inngangsvariabelen x.

- Oppgave 2

Finn krysset mellom funksjonene f (x) = 5 og G (x) = 5x - 2

Løsning

For å finne skjæringspunktet mellom disse to funksjonene, kan de omskrives på henholdsvis:

y = 5; y = 5x - 2

De er matchet, skaffer seg:

5x - 2 = 5

Som er en lineær ligning av første grad, hvis løsning er:

5x = 5+2 = 7

x = 7/5

Krysspunktet er (7/5; 5).

- Øvelse 3

Demonstrere at den som er avledet fra en konstant funksjon er 0.

Løsning

Fra definisjonen av derivat har du:

 f (x) = k

f (x+h) = k

Erstatte definisjonen:

Ovennevnte er fornuftig, siden derivatet av en funksjon er definert som skråningen på linjen Tangent til kurven på et gitt punkt. Den konstante funksjonen har en null i påvente og enhver tangent linje til den også.

I tillegg, hvis vi tenker på derivatet som en valutakurs Dy/dx, Den konstante funksjonen opplever ingen endring, derfor er derivatet ugyldig.

Kan tjene deg: Multiplikativ prinsipp: telleteknikker og eksempler

- Oppgave 4

Finn det ubestemte integralet av f (x) = k.

Løsning

- Oppgave 5

Et mobiltelefonselskap tilbyr ubegrenset internettjeneste med fast pris som betaler $ 15 per måned. Hva er prisfunksjonen i henhold til tiden?

Løsning

La P være prisen som skal betales til $ og t tid, som kan uttrykkes i dager. Funksjonen er etablert som følger:

P (t) = 15

- Oppgave 6

Følgende kontra tidsgraf tilsvarer bevegelsen av en partikkel.

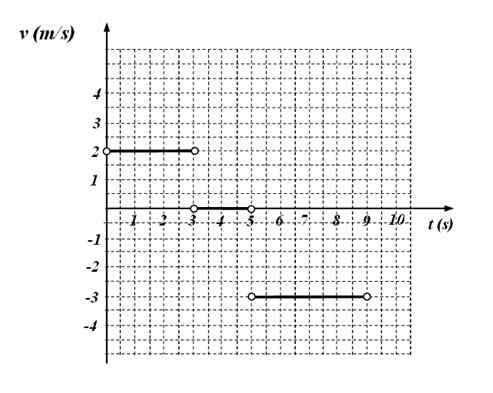Figur 4. Funksjon V (t) Funksjonsgraf for øvelse 6. Kilde: f. Zapata.

Det blir bedt om:

a) Skriv et uttrykk for hastighetsfunksjon som en funksjon av tid V (t).

b) Finn avstanden som er reist av mobilen i tidsintervallet mellom 0 og 9 sekunder.

Løsning på

Av grafen som viser det:

-V = 2 m/s I tidsintervallet mellom 0 og 3 sekunder

-Mobilen er varetektsfengslet mellom 3 og 5 sekunder, siden hastigheten i dette intervallet er verdt 0.

-V = - 3 m/s Mellom 5 og 9 sekunder.

Det er et eksempel på et stykke stykker, eller funksjon i deler, som igjen er sammensatt av konstante funksjoner, bare gyldige for de angitte tidsintervallene. Det konkluderes med at den etterspurte funksjonen er:

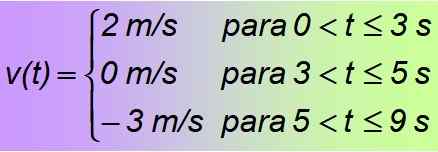
Løsning b

Fra graf V (t) kan avstanden som er reist av mobilen beregnes, noe som numerisk tilsvarer området lavt/på kurven. Denne måten:

-Avstand reist mellom 0 og 3 sekunder = 2 m/s . 3 s = 6 m

-Mellom 3 og 5 sekunder ble han varetektsfengslet, derfor reiste han ingen avstand.

-Avstand reist mellom 5 og 9 sekunder = 3 m/s . 4 s = 12 m

Totalt turnerte mobilen 18 m. Se at selv om hastigheten er negativ i intervallet mellom 5 og 9 sekunder, er avstanden som er reist positiv. Det som skjer er at i løpet av det tidsintervallet hadde mobilen endret betydningen av hastigheten.

Referanser

1. Geogebra. Konstante funksjoner. Gjenopprettet fra: Geogebra.org.
2. Maplesoft. Den konstante funksjonen. Gjenopprettet fra: Maplesoft.com.
3. Wikilibros. Beregning i en variabel/funksjoner/konstant funksjon. Gjenopprettet fra: er.Wikibooks.org.
4. Wikipedia. Konstant funksjon. Hentet fra: i.Wikipedia.org
5. Wikipedia. Konstant funksjon. Gjenopprettet fra: er.Wikipedia.org.