Avtagende funksjon Hvordan identifisere den, eksempler, øvelser

EN avtagende funksjon f er en hvis verdi reduseres når verdien av x øker. Betyr at i et gitt intervall, med tanke på to verdier x₁ og x₂ slik at x₁ < x₂, deretter f (x₁)> f (x₂).

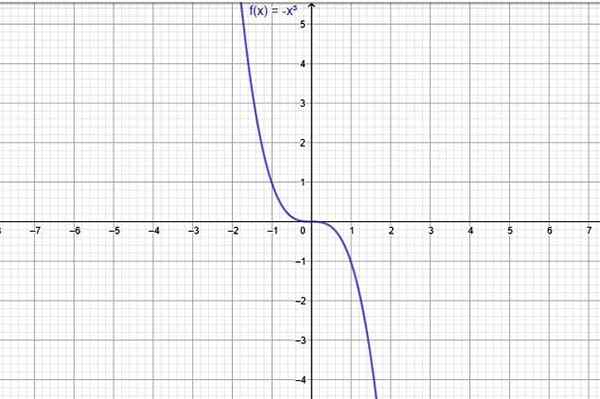
Et eksempel på en funksjon som alltid synker er f (x) = -x³, hvis graf viser i følgende figur:

Figur 1. En funksjon som alltid avtar i hele domenet er f (x) = -x^3. Kilde: f. Zapata gjennom Geogebra.

Selv om noen funksjoner som dette er preget av å være avtagende i alt sitt domene, oppfører ikke alle seg slik, er det økende og også de som vokser og reduseres i visse domeneintervaller. Studien av vekst og reduseringsintervaller kalles monotoni av funksjonen.

På samme måte kan veksten eller reduksjonen av funksjonen vurderes på et bestemt domenepunkt. Men enhver funksjon som synker i et gitt intervall, er også på hvert punkt som tilhører den.

[TOC]

Hvordan identifisere en avtagende funksjon?

Funksjonsgrafen indikerer visuelt om den synker eller ikke. Hvis når du beveger seg i den økende forstand av X, "stiger" -funksjonen, betyr det at den avtar.

Og hvis du har intervaller der det avtar og vokser vekselvis, som er det mest vanlige, fordi disse tydelig blir avslørt ved å observere oppførselen til funksjonen gjennom hele domenet, siden det vil være intervaller der funksjonen "stiger opp" og andre i som "ned".

Alternativt, hvis funksjonsgrafen ikke er tilgjengelig, er det analytisk mulig å avgjøre om den avtar på et tidspunkt eller i et intervall, gjennom det første derivatet.

Kriterium for det første derivatet

Legg merke til oppførselen til den avtagende funksjonen vist i figur 2. De rosa linjesegmentene er tangente til punktene hvis koordinater er [a, f (a)] og [A+H, F (A+H)] og ha en negativ skråning.

Kan tjene deg: Hvordan er informasjonen innhentet i en undersøkelse?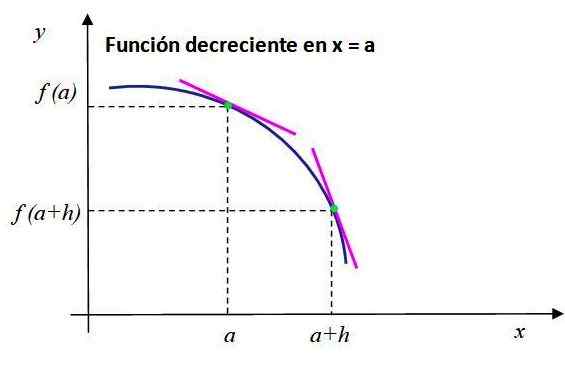Figur 2. Hellingen av tangentlinjen til grafen til F (x) er negativ ved x = a, så avtar funksjonen på dette tidspunktet. Kilde: f. Zapata.

For denne funksjonen er følgende oppfylt:

F (a+h) - f (a) < 0 ⇒  F (a+h) < f (a)

Derfor kan det tenkes at funksjonen synker i x = a.

Imidlertid er den første avledet fra funksjonen f (x), evaluert ved x = a, som per definisjon er helningen på tangentlinjen til kurven ved x = a, gitt av:

Grensen indikerer at verdien av h kan gjøres så liten du vil og antyder at tegnet på fa), Det kan brukes til å vite om funksjonen synker på et bestemt punkt eller ikke, så lenge derivatet eksisterer på det tidspunktet.

Da ja fa) < 0, Det kan bekreftes at funksjonen synker, og tvert imot, hvis f '(a)> 0, Da vokser funksjonen på det tidspunktet.

Teorem for å redusere og vokse funksjoner

Tidligere ble det henvist til oppførselen til funksjonen på et punkt. Nå tillater følgende teorem å kjenne intervallene der en funksjon synker, vokser eller konstant:

La f være en differensiell funksjon i intervallet (a, b). Det er sant, det:

-Ja f '(x) < 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Hvis tvert imot f '(x)> 0 for alle x som tilhører (a, b), sies det at funksjonen f (x) vokser inn (a, b).

-Til slutt, hvis f '(x) = 0 for alle x som tilhører intervallet (a, b), er f (x) konstant i nevnte intervall.

Demonstrasjon

Anta at f '(x) < 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ og x₂ tilhører nevnte intervall og tilstanden som x₁< x₂.

Gjennomsnittsverdi -teorem sier at det er et reelt tall C, mellom x₁ og x₂, slik at:

Kan tjene deg: Vanlig faktor for gruppering av begreper: eksempler, øvelser

Som etablert siden x₁< x₂,  Δx er positiv. Så som f '(c) er negativ, så er det også. Derfor f (x₁) er større enn f (x₂) Og funksjonen avtar effektivt på alle punkt i intervallet (a, b).

Trinn for å vite om en funksjon synker

For å finne intervallene for reduksjon og vekst av en funksjon ved å bruke forrige teorem, følges disse trinnene:

-Finn den første avledet fra funksjonen og match den til null, og løser den resulterende ligningen. Bestem også punktene der derivatet ikke eksisterer.

Alle disse punktene kalles Kritiske punkter Og det er nødvendig å finne dem, siden derivatet i dem har muligheten til å endre tegnet sitt, noe som indikerer at funksjonen går fra å vokse til å synke eller tvert imot.

-Funksjonens domene er delt inn i intervaller bestemt av punktene der det første derivatet blir kansellert eller ikke eksisterer.

-Til slutt blir tegnet på derivatet studert på et vilkårlig punkt som tilhører hvert av intervallene oppnådd i forrige trinn.

Eksempler på synkende funksjoner

Funksjonene avtar ikke alle i samme takt, noen gjør det raskere enn andre. Følgende funksjoner, som vises ofte i praksis, synker:

Eksponentiell funksjon

En funksjon av form f (x) = a^x, Med en mellom 0 og 1, ikke inkludert disse, reduseres raskt gjennom hele domenet.

Funksjon 1/x

Gjennom et online grafisk program som geogebra er grafen til funksjonen f (x) = 1/x bygget, og bekrefter at den synker i hele sitt domene.

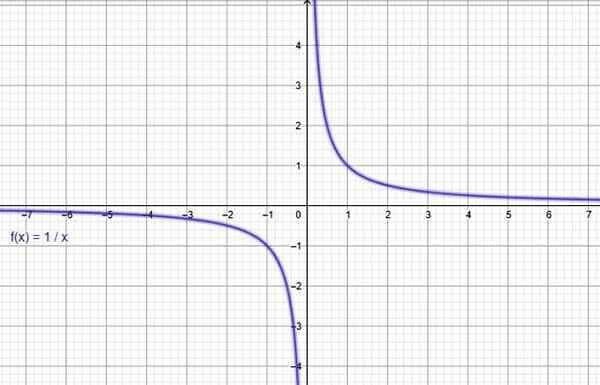Figur 3. Funksjonen f (x) = 1/x synker. Kilde: f. Zapata gjennom Geogebra.

Den relaterte funksjonen

Funksjonene til formen y = mx + b med m<0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Kan tjene deg: matematisk likhet

Trening løst

Finn, om noen, reduseringsintervallene til funksjonen:

f (x) = x⁴ - 6x² - 4

Løsning

Det første trinnet er å finne f '(x):

f '(x) = 4x³ - 12x

Det første derivatet av F (x) er en kontinuerlig funksjon, det vil si at den ikke har noen diskontinuitetspunkter, men blir kansellert inn:

4x³ - 12x = 0 = 4x (x²-3) = 0

Løsningene av denne ligningen er: x₁ = 0, x₂ = - √3 og x₃ = √3. Dette er de kritiske punktene, som deler domenet til f (x) i intervallene: (-∞,- √3); (- √3.0); (0, √3); (√3, ∞+).

Deretter blir den første avledet i en vilkårlig x -verdi evaluert, som tilhører hvert intervall. Disse verdiene ble valgt:

For (-∞,- √3)

F '(-2) = 4 (-2)³ - 12x (-2) = -32+24 = -8

For (- √3.0)

F '(-1) = 4 (-1)³ - 12x (-1) = -4+12 = 8

For (0, √3)

f '(1) = 4 (1)³ - 12x (1) = 4-12 = -8

For (√3, ∞+)

f '(2) = 4 (2)³ - 12x (2) = 32-24 = 8

Som flere intervaller er det lurt å lage et bord for å organisere resultatene. Pilen oppover indikerer at funksjonen vokser og ned, noe som avtar:

Det konkluderes med at funksjonen avtar med intervallene (-∞,- √3) og (0, √3) og vokser i de gjenværende intervallene. Den opprinnelige funksjonen i Geogebra blir enkelt sjekket ved grafing.

Referanser

1. Ayres, f. 2000. Beregning. 5ed. Mc Graw Hill.
2. Leithold, l. 1992. Beregning med analytisk geometri. Harla, s.TIL.
3. Purcell, e. J., Varberg, d., & Rigdon, s. OG. (2007). Beregning. Mexico: Pearson Education.
4. Matemobile. Funksjoner, voksende, synkende og konstant. Gjenopprettet fra: Matemovil.com
5. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.