Homografisk funksjon hvordan graf, løste øvelser

De funksjonHomografisk eller rasjonell Ón Det er en type matematisk funksjon sammensatt av delingen av to polynomkomponenter. Det adlyder formen P (x)/q (x), der q (x) ikke kan ta nullform.

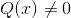
For eksempel tilsvarer uttrykket (2x - 1)/(x + 3) en homografisk funksjon med p (x) = 2x - 1 y q (x) = x + 3.

Kilde: Pixabay.com

Homografiske funksjoner utgjør en studiedel av analytiske funksjoner, som blir behandlet fra grafisk tilnærming og fra domenet og rekkevidde studien. Dette skyldes begrensningene og fundamentene som må brukes for deres resolusjoner.

[TOC]

Hva er en homografisk funksjon?

De er rasjonelle uttrykk for unik variabel, selv om dette ikke betyr at det ikke er noe lignende uttrykk for to eller flere variabler, der det allerede vil være i nærvær av kropper i rommet som adlyder de samme mønstrene som den homografiske funksjonen i nivået.

De har reelle røtter i noen tilfeller, men eksistensen av vertikale og horisontale asymptoter opprettholdes alltid, samt også vekst og reduser intervaller. Vanligvis er bare en av disse trendene til stede, men det er uttrykk som er i stand til å vise begge i deres utvikling.

Hans domene er begrenset av røttene til nevneren, fordi det ikke er noen inndeling mellom null av reelle tall.

Blandet homografisk funksjon

De er veldig hyppige i beregningen, spesielt differensial og omfattende, og er nødvendige for å utlede og anti -mangel under spesielle formler. Noen av de vanligste er klassifisert nedenfor.

Nth par homografisk funksjon

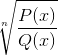
Ekskluderer alle elementene i domenet som gjør argumentet negativt. Røttene som er til stede i hvert polynomisk viser nullverdier når de blir evaluert.

Disse verdiene aksepteres av radikalen, selv om den grunnleggende begrensningen av den homografiske funksjonen bør vurderes. Der q (x) ikke kan motta nullverdier.

Kan tjene deg: Transcendente funksjoner: Typer, definisjon, egenskaper, eksempler

Intervallløsninger må avskjæres:

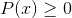
For å oppnå kryss, kan tegnmetoden brukes, blant andre.

Homografisk funksjonslogaritme

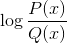
Ekskluderer domeneverdiene som kaster negative intervaller og nuller. Fordi nuller allerede er ekskludert fra nevneren, er løsningene av: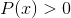

Det er også vanlig å finne begge uttrykkene i ett, blant andre mulige kombinasjoner.

Hvordan tegne en homografisk funksjon?

Homografiske funksjoner samsvarer grafisk med hyperboler i flyet. Som transporteres horisontalt og vertikalt i henhold til verdiene som definerer polynomene.

Det er flere elementer som vi må definere for å tegne en rasjonell eller homografisk funksjon.

Eiendom

Den første vil være røttene eller nulene til funksjonene P og Q.

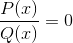
Verdiene oppnådd vil bli betegnet på x -aksen til grafikken. Som indikerer kryssene mellom grafen med aksen.

Vertikal asymptote

Samsvarer med vertikale linjer, som avgrenser grafen i henhold til trendene de presenterer. De berører x -aksen i verdiene som gjør nevneren null og vil aldri bli berørt av grafen til den homografiske funksjonen.

Horisontal asymptote

Representert med en horisontal stinglinje, avgrenset en grense som funksjonen ikke vil bli definert på det nøyaktige punktet. Trender vil bli observert før og etter denne linjen.

For å beregne det må vi ty til en metode som ligner på L'Hopital -metoden, brukt for å løse rasjonelle funksjonsgrenser som har en tendens til uendelig. Koeffisientene til de høyeste kreftene i telleren og denominatoren til funksjonen må tas.

For eksempel har følgende uttrykk en horisontal asymptot ved y = 2/1 = 2.

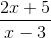
Vekstintervall

Verdiene til de bestilte vil ha trender merket i grafen på grunn av asymptotene. Når det gjelder vekst, vil funksjonen øke fra verdier når elementene i domenet fra venstre til høyre blir evaluert.

Kan tjene deg: 60 deling

Avtagende intervall

Bestilte verdier vil avta når elementene i domenet fra venstre til høyre blir evaluert.

Hoppene som finnes i verdiene vil ikke bli tatt i betraktning når det øker eller reduseres. Dette skjer når grafen er nær en vertikal eller horisont.

Kryss med y

Å gjøre null verdien av x, er krysset med ordinatene. Dette er et veldig nyttig faktum for å skaffe grafen til den rasjonelle funksjonen.

Eksempler

Definer grafen for følgende uttrykk, finn røttene, vertikale og horisontale asymptoter, vekst og reduser intervaller og kryss med den bestilte aksen.

Oppgave 1

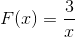
Uttrykket mangler røtter, fordi det har en konstant verdi i telleren. Begrensningen som skal brukes vil være x forskjellig fra null. Med horisontal asymptote ved y = 0, og asymptot vertikal ved x = 0. Det er ingen skjæringspunkter med aksen og.

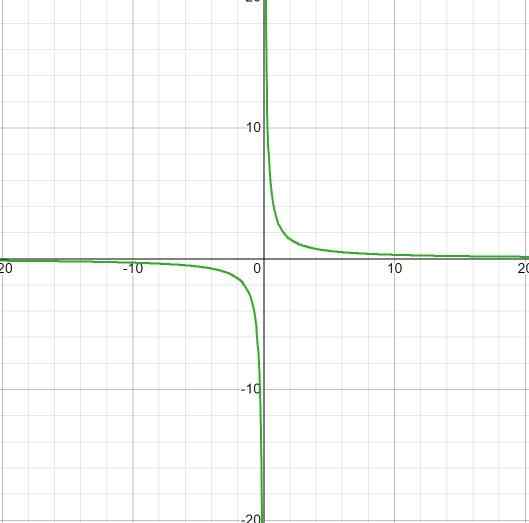
Det observeres at det ikke er noen vekstintervaller selv med hoppet fra mindre til mer uendelig i x = 0.

Reduksjonsintervallet er

Id: (-∞; o) u (0, ∞)

Oppgave 1.2

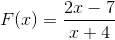
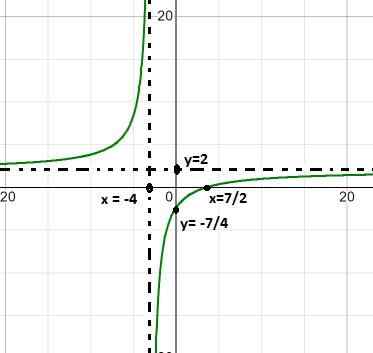
2 polynomer blir observert som i den første definisjonen, så vi fortsetter i henhold til de etablerte trinnene.

Roten som er funnet er x = 7/2 som er resultatet av å utjevne funksjonen.

Den vertikale asymptoten er på x = - 4, som er verdien ekskludert fra domenet på grunn av den rasjonelle funksjonstilstanden.

Den horisontale asymptoten er i y = 2, dette etter å ha delt 2/1, koeffisientene til grad 1 -variablene.

Den har et kryss med de som er bestilt på Y = - 7/4. Verdien funnet etter utjevning av x til null.

Det kan tjene deg: brøkdel tilsvarer 3/5 (løsning og forklaring)

Funksjonen vokser konstant, med et hopp fra mer til mindre uendelig rundt roten x = -4.

Vekstintervallet er (-∞, - 4) u ( - 4, ∞).

Når verdien av x er nær mindre uendelig, tar funksjonen verdier nær 2. Det samme skjer når X nærmer seg mer uendelig.

Uttrykket nærmer seg mer uendelig når det blir evaluert i - 4 til venstre, og mindre uendelig når det blir evaluert i - 4 til høyre.

Oppgave 2

Grafen for følgende homografiske funksjon observeres:

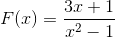
Beskriv deres oppførsel, røtter, vertikale og horisontale asymptoter, vekst og reduser intervaller og kryss med den bestilte aksen.

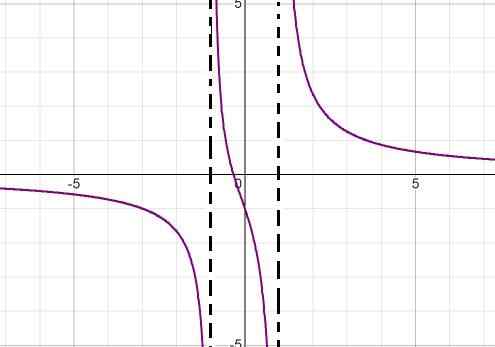
Uttrykket nevner denominator. På denne måten kan begge vertikale asymptoter defineres som:

x = -1 og x = 1

Den horisontale asymptoten tilsvarer Abscissa -aksen fordi hovedkraften er i nevneren.

Den eneste roten er definert av x = -1/3.

Uttrykket avtar alltid fra venstre mot høyre. Den nærmer seg null når det har en tendens til uendelig. Mindre uendelig når du nærmer deg -1 til venstre. Mer uendelig når du nærmer deg -1 til høyre. Mindre uendelig når du nærmer deg 1 til venstre og mer uendelig når du nærmer deg 1 til høyre.

Referanser

1. Tilnærming med rasjonelle funksjoner. Donald J. Ny mann. American Mathematical Soc., 31. desember. 1979
2. Ortogonale vurderingsfunksjoner. University of La Laguna Tenerife Adhemar Bultheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njstad. Cambridge University Press, 13. februar. 1999
3. Vurdering tilnærming av reelle funksjoner. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. mars. 2011
4. Algebraiske funksjoner. Gilbert Ames Bliss. Couer Corporation, 1. januar. 2004
5. Spanish Mathematical Society Magazine, 5-6 bind. Spanish Mathematical Society, Madrid 1916