Transcendente funksjoner typer, definisjon, egenskaper, eksempler

De transcendente funksjoner Elementals er eksponentielle, logaritmiske, trigonometriske, inverse trigonometriske funksjoner, hyperbolsk og omvendt hyperbolsk. Det vil si at de er de som ikke kan uttrykkes av et polynom, et polynom- eller polynom røtter forhold. 

De ikke-elementære transcendente funksjonene er også kjent som spesielle funksjoner, og blant dem kan feilfunksjonen navngis. De Algebraiske funksjoner (Polynomer, polynomkvotienter og polynomerøtter) ved siden av transcendente funksjoner Elementals utgjør det som i matematikk er kjent som Elementære funksjoner.

Det anses også som transcendente funksjoner som følger av operasjoner mellom transcendente funksjoner eller mellom transcendente og algebraiske funksjoner. Disse operasjonene er: summen og forskjellen på funksjoner, produkt og forhold mellom funksjoner, samt sammensetningen av to eller flere funksjoner.

[TOC]

Definisjon og egenskaper

Eksponentiell funksjon

Det er en reell funksjon av ekte uavhengig variabel av skjemaet:

f (x) = a^x = a^x

hvor til Det er et positivt reelt tall (A> 0) fast kalt basen. Circumflejo eller tilsyn brukes til å betegne potensieringsoperasjonen.

La oss sette i tilfelle A = 2 Da er funksjonen slik:

f (x) = 2^x = 2^x

Som vil bli evaluert for flere verdier av den uavhengige variabelen x:

Nedenfor er en grafikk der eksponentiell funksjon for flere baseverdier er representert, inkludert basen og (Nepernummer og ≃ 2.72). Utgangspunkt og Det er så viktig at generelt når du snakker om eksponentiell funksjon, tenker du på E^x, som også er betegnet exp (x).

Figur 1. Eksponentiell funksjon a^x, for flere verdier av basen a. (Egen utdyping)

Eksponentielle funksjonsegenskaper

Fra figur 1 kan det sees at domenet til eksponentielle funksjoner er reelle tall (DOM F = R) og rekkevidden eller ruten er de positive virkelige (løp F = R⁺). 

Kan tjene deg: symmetri

På den annen side, uavhengig av verdien av base A, går alle eksponentielle funksjoner gjennom punktet (0, 1) og etter punkt (1, a). 

Når basen A> 1, Da vokser funksjonen og når 0 < a < 1 Funksjonen avtar. 

Kurvene til y = a^x og av y = (1/a)^x  De er symmetriske med hensyn til aksen OG. 

Med unntak av saken A = 1, Den eksponentielle funksjonen er injiserende, det vil si til hver verdi av bildet, en tilsvarer og bare en startverdi.

Logaritmisk funksjon

Det er en reell faktisk funksjon av ekte uavhengig variabel basert på definisjonen av logaritmen til et tall. Logaritme basert til av et tall x, Det er tallet og som basen må heves for å få argumentet x:

Logg_til(x) = y ⇔ a^y = x

Det er det Logaritmefunksjon i base til Det er den omvendte funksjonen til eksponentiell funksjon basert på til.

For eksempel:

Logg₂1 = 0, siden 2^0 = 1

En annen sak, logg₂4 = 2, fordi 2^2 = 4

Rotlogaritmen til 2 er logg₂√2 = ½, fordi 2^½ = √2

Logg₂ ¼ = -2, med tanke på at 2^(-2) = ¼ 

Nedenfor er en graf over logaritmefunksjonen i forskjellige baser.

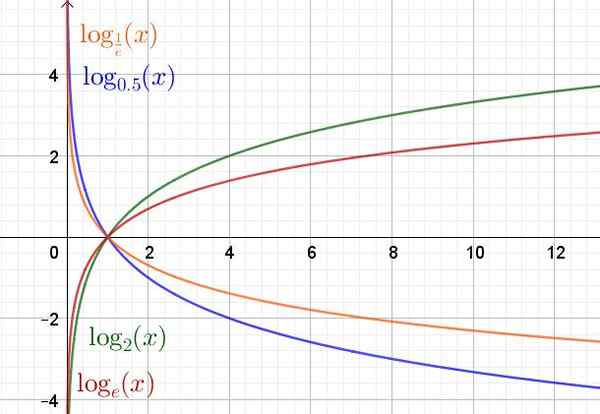Figur 2. Eksponentiell funksjon for forskjellige basisverdier. (Egen utdyping)

Logaritmo -funksjonsegenskaper

Domenet til logaritmefunksjonen og (x) = logtil(x)  De er de positive reelle tallene R+. Rekkevidden eller ruten er de reelle tallene R.

Uansett base går logaritmefunksjonen alltid gjennom punktet (1.0) og punktet (a, 1) tilhører grafen til nevnte funksjon.

Det kan tjene deg: køteori: historie, modell, hva er det for og eksempler for

I tilfelle at base A er større enn enheten (a> 1) øker logaritmefunksjonen. Men ja (0 < a < 1) entonces es una función decreciente.

Seno, Coseno og Tangent Functions

Sinusfunksjonen tildeler et reelt tall og til hver verdi x, der x representerer målet på en vinkel i radianer. For å oppnå verdien av sen (x) fra en vinkel, er vinkelen representert i enhetssirkelen og projeksjonen av nevnte vinkel på den vertikale aksen er brystet som tilsvarer den vinkelen.

Nedenfor er (i figur 3) den trigonometriske sirkelen og brystet for flere vinkelverdier x1, x2, x3 og x4.

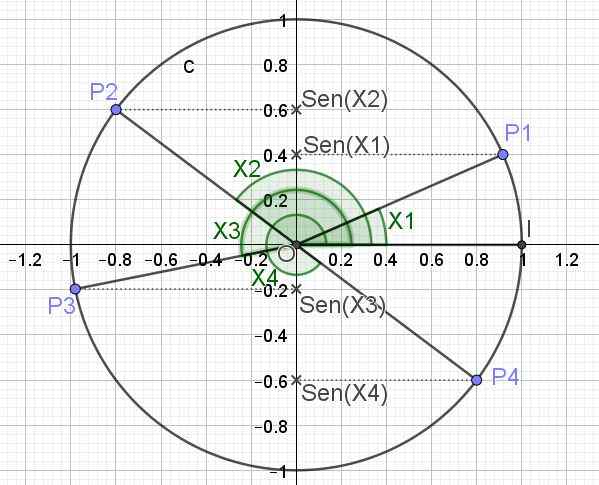Figur 3. Trigonometrisk sirkel og barm av flere vinkler. (Egen utdyping)

Definert på denne måten den maksimale verdien som Sen (x) -funksjonen kan ha er 1, som oppstår når x = π/2 + 2π n, er n et heltall (0, ± 1, ± 2,). Minimumsverdien som Sen (x) -funksjonen kan ta når x = 3π/2 + 2π n. 

Coseno y = cos (x) -funksjonen er definert på lignende måte, men projeksjonen av vinkelposisjonene P1, P2, etc. utføres på den horisontale aksen til den trigonometriske sirkelen.

På den annen side er Y = Tan (x) -funksjonen forholdet mellom sinusfunksjonen og kosinusfunksjonen.

Deretter vises en graf over de transcendente funksjonene sen (x), cos (x) og tan (x)

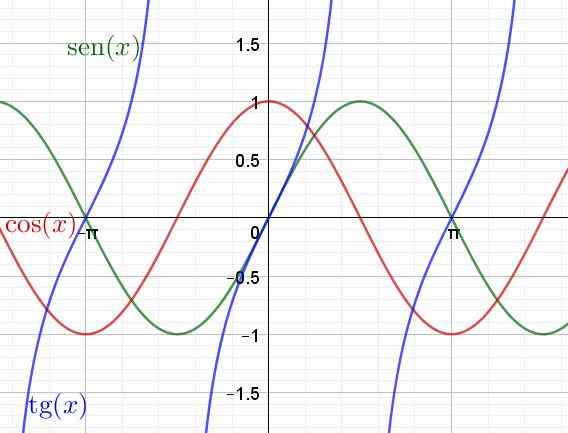Figur 4. Graf over transcendente funksjoner, bryst, kosinus og tangent. (Egen utdyping)

Avledet og integrert

Avledet fra eksponentiell funksjon

Derivatet og' av eksponentiell funksjon y = a^x Det er funksjonen a^x multiplisert av ham Neperisk logaritme av basen a:

Kan tjene deg: sett teori: egenskaper, elementer, eksempler, øvelser

og '= (a^x)' = a^x ln a

I det spesielle tilfellet av basen og, Derivatet av eksponentiell funksjon er selve eksponentiell funksjon.

Integrert av eksponentiell funksjon

Det ubestemte integralet av a^x Det er funksjonen som er delt mellom den neperiske logaritmen til basen. 

I det spesielle tilfellet med base E er integralen av eksponentiell funksjon den eksponentielle funksjonen i seg selv.

Derivat og integrert tabell over de transcendente funksjonene

Nedenfor er en sammendrag av tabellen over de viktigste transcendente funksjonene, dens derivater og ubestemte (antiderivater):

Ubestemt derivat og integrert tabell for noen transcendente funksjoner. (Egen utdyping)

Eksempler

Eksempel 1

Finn den resulterende funksjonen til sammensetningen av funksjonen f (x) = x^3 med funksjonen g (x) = cos (x):

(f eller g) (x) = f (g (x)) = cos³(x)

Dens derivat og dets ubestemte integral er:

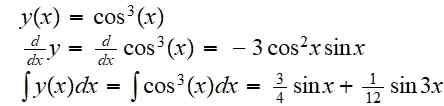
Eksempel 2

Finn sammensetningen av G -funksjonen med F -funksjonen, være G og F funksjonene som er definert i forrige eksempel:

(g eller f) (x) = g (f (x)) = cos (x³)

Det skal bemerkes at sammensetningen av funksjoner ikke er en kommutativ operasjon.

Derivatet og det ubestemte integralet for denne funksjonen er henholdsvis:

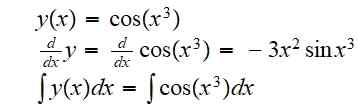
Integralen ble igjen indikert fordi det ikke er mulig å skrive resultatet som en kombinasjon av elementære funksjoner på en nøyaktig måte.

Referanser

1. Beregning av en enkelt variabel. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. nov. 2008
2. Den implisitte funksjonsteoremet: Historie, teori og applikasjoner. Steven G. Krantz, Harold R. Parker. Springer Science & Business Media, 9. nov. 2012
3. Multivariabel analyse. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. desember. 2010
4. Systemdynamikk: Modellering, simulering og kontroll av mekatroniske systemer. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. mars. 2012
5. Kalkulus: Matematikk og modellering. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. januar. 1999
6. Wikipedia. Transcendent funksjon. Gjenopprettet fra: er.Wikipedia.com