Grunnleggende trigonometriske funksjoner, i det kartesiske planet, eksempler, trening

De trigonometriske funksjoner Av ekte variabel tilsvarer de enhver vinkel (uttrykt i radianer), en trigonometrisk grunn, som kan være sinus, kosinus, tangent, cotangent, secant og høst.

På denne måten har vi de seks trigonometriske funksjonene: bihule, kosinus, tangent, høsting, tørking og cotangent.

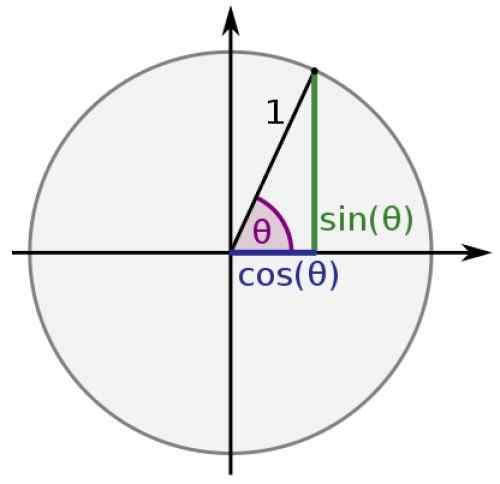
Figur 1. Trigonometric Circle Animation. Kilde: Wikimedia Commons.

De trigonometriske funksjonene for vinkler mellom 0 og 2π er definert ved hjelp av den enhetlige omkretsen, av radio 1 og hvis sentrum sammenfaller med opprinnelsen til det kartesiske koordinatsystemet: poenget (0.0).

Vi kan finne et hvilket som helst punkt P for koordinater (x, y) på denne omkretsen.

Segmentet som forener opprinnelsen med P, sammen med de respektive segmentene som forener fremskrivningene av P på koordinataksene, utgjør en rektangel -trekant, hvis trigonometriske grunner er kjent som kvotientene mellom sidene av trekanten. Så:

• sin θ = motsatt /hypotenusa kateto
• cos θ = tilstøtende /hypotenusa kateto
• tg θ = motsatt kateto /tilstøtende kateto

Og nå er årsakene til det omvendte av det ovennevnte:

• Sec θ = hypotenuse /tilstøtende kateto
• Skade θ = hypotenusa /kateto motsatt
• ctg θ = tilstøtende kateto /motsatt kateto

I den enhetlige sirkelen er hypotenusen til enhver trekant lik 1 og kategoriene er verdt x og y, da:

sin θ = y

cos θ = x

Figur 2. Høyre trekant i enhetssirkelen. Kilde: Wikimedia Commons.

På denne måten skaffer Sine og Cosine -funksjonene alltid verdier mellom -1 og 1, mens de gjenværende:

tg θ = y/x

skade θ = 1/y

Sek θ = 1/x

De er ikke definert når x enten og De er verdt 0.

[TOC]

Trigonometriske funksjoner i det kartesiske planet

Som vi vil se nedenfor, er trigonometriske funksjoner preget av å være periodisk. Derfor er de ikke bijektive, bortsett fra i et begrenset domene.

Funksjon f (x) = sin x

Fra og med den trigonometriske sirkelen ved punkt P (1.0), er vinkelen 0 radianer. Deretter roterer radius i en anti -Horary forstand og Sen X -funksjonen vokser gradvis til den når π/2 -radianer (90º), tilsvarer 1.Omtrent 571 radianer.

Kan tjene deg: Tilleggsvinkler: Hva er, beregning, eksempler, øvelser

Der når den verdien y = 1 og deretter avtar den til den når null i π -radianer (180 °). Deretter avtar det enda mer, siden verdien blir negativ til han når −1 når vinkelen er 3π/2 radianer (270 °).

Til slutt øker det igjen til det går tilbake til null i 360 °, der alt starter igjen. Dette gjør y = sin x a periodisk funksjon av periode 2π, så bihulefunksjonen er ikke bijektiv.

I tillegg er grafen symmetrisk med hensyn til punktet (0,0), derfor er funksjonen merkelig.

Så grafen til y = sen x:

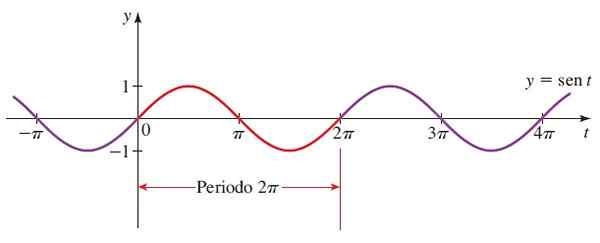Figur 3. Funksjonsgraf f (x) = sin x. Kilde: Stewart, J. Precculment: Matematikk for universitetet.

Den røde delen er den første perioden. Negative vinkler blir også vurdert, siden radiusen til den trigonometriske sirkelen kan rotere i en timeplan.

Sen x domene = Alle reales.

Sen x rekkevidde eller rute = [-1,1]

Funksjon f (x) = cos x

Ved punkt P (1.0) er coseno -funksjonen verdt 1 og derfra avtar, når 0 når vinkelen er π/2. Fortsett å avta og tar negative verdier, til du når -1 i vinkel π.

Så begynner det å øke gradvis til den når 0 i 3π/2 og tar verdi igjen når radius har vendt en fullstendig sving. Derfra gjentas syklusen, siden cos x er periodisk og også er dreiemoment (symmetrisk rundt den vertikale aksen).

Formen av kosinusfunksjonen er den samme som bihulefunksjonen, med mindre de er fortrengt π/2 en med hensyn til den andre.

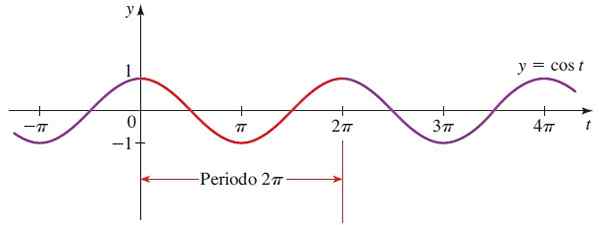Figur 4. Funksjonsgraf f (x) = sin x. Kilde: Stewart, J. Precculment: Matematikk for universitetet.

Cos x domene = Alle reales.

Kan tjene deg: punktlig estimat

Rekkevidde eller cos x rute = [-1,1]

Diskontinuerlige trigonometriske funksjoner

Funksjonene TG X, CTG X, SEC X og HARS. Siden disse er verdt 0 i noen vinkler, når de vises i nevneren, gjør de funksjonen diskontinuerlig.

Og siden bihule og kosinus er periodiske funksjoner, er også funksjonene Tg X, CTG X, SEC X, skade x.

Tangentfunksjon f (x) = tg x

For tangentfunksjonen er diskontinuitetsverdiene: ± π/2, ± 3π/2, ± 5π/2 ... Der tar funksjonen veldig store eller veldig små verdier. Generelt skjer dette for alle multipler av π av formen (2n+1) π/2, både positive og negative, med n = 0, 1, 2 ..

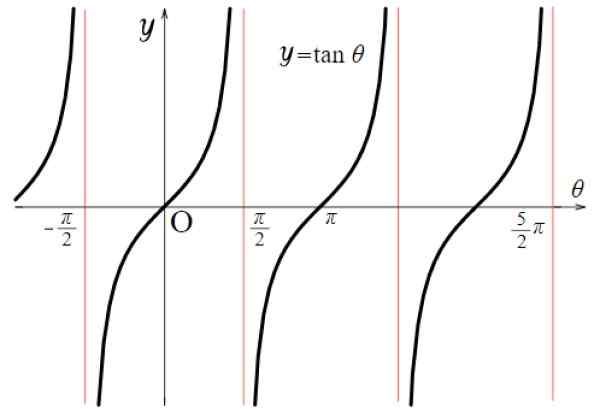Figur 5. Funksjonsgraf f (x) = tg x. Kilde: Wikimedia Commons.

Derfor:

TG X -domene: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Rang eller TG X -turné: Alle reales.

Merk at funksjonen f (x) = tg x gjentas mellom - π/2 og + π/2, derfor er perioden π. I tillegg er det symmetrisk med hensyn til opprinnelsen.

Cotangent funksjon f (x) = ctg x

For denne funksjonen forekommer diskontinuitetsverdier i 0, ± π, ± 2π…, det vil si hele multiplene av π.

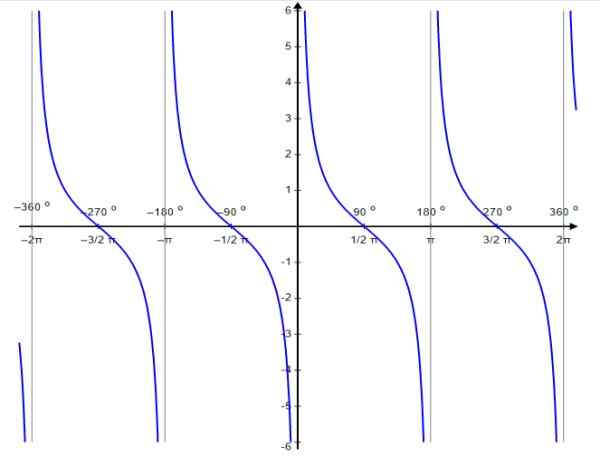Figur 6. Funksjonsgraf f (x) = cotg x. Kilde: Wikimedia Commons.

Som tangentfunksjonen er den kotangente funksjonen periodisk periode π. For henne er det oppfylt at:

CTG X -domene: D = x ∈ R / x ≠ n π; n ∈ Z

CTG X -rekkevidde eller rute: Alle reales.

Tørkefunksjon f (x) = sek x

SEC X -funksjonen har diskontinuitetspunkter i ± π/2, ± 3π/2, ± 5π/2…, hvor cos x = 0. Det er også periodisk periode π og observeres også av grafen at funksjonen aldri tar verdier i intervallet (-1,1)

Kan tjene deg: Hele tall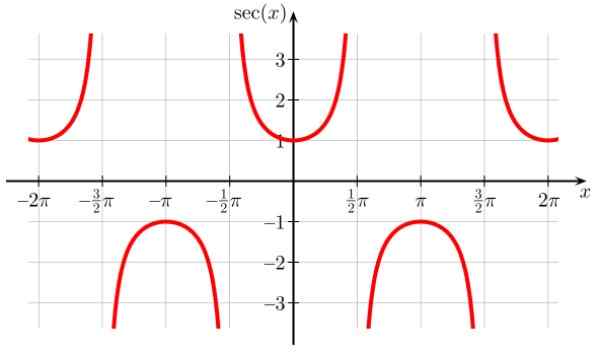 Figur 7. Funksjonsgraf f (x) = sek x. Kilde: Wikimedia Commons.

Doma av sek X: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

SEC X -rekkevidde eller rute: Alle reais unntatt (-1,1)

Høstfunksjon f (x) = skade x

Det ligner på tørkefunksjonen, selv om den er forskjøvet til høyre, derfor er diskontinuitetspunktene 0, ± π, ± 2π og alle hele multiplene av π. Det er også periodisk.

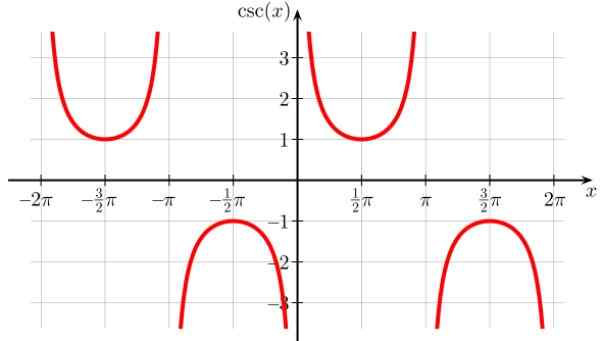Figur 8. Funksjonsgraf f (x) = skade x. Kilde: Wikimedia Commons. Geek3/CC By-SA (https: // CreativeCommons.Org/lisenser/by-SA/4.0)

Skade domene x: D = x ∈ R / x ≠ n π; n ∈ Z

Rekkevidde eller harmonirute: Alle reais unntatt (-1,1)

Trening løst

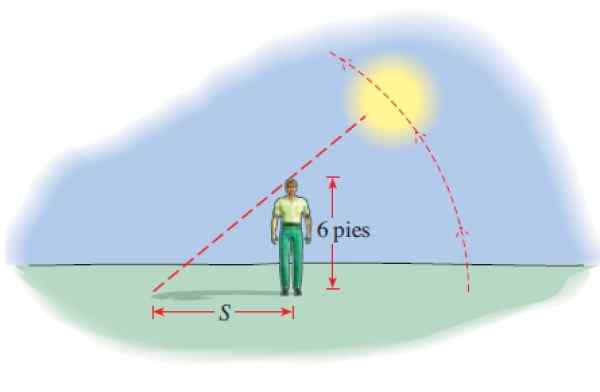
En 6 -fot høy mann projiserer en skygge som har lengde av:

S (t) = 6 │cot (π.T/12) │

Med S ved føtter og t antall timer etter 06.00. Hvor mye er skyggen klokka 8, klokka 12, kl. 14 og klokken 17:45?

Løsning

Vi må evaluere funksjonen for hver av de gitte verdiene, merk at den absolutte verdien må ta, siden skyggens lengde er positiv:

-08.00 er det gått 2 timer fra 06.00, derfor er t = 2 og s (t):

S (2) = 6 │cot (π.2/12) │pies = 6 │cot (π/6) │pies = 10.39 fot.

-Når det er 12 n, har t = 6 timer gått, derfor:

S (6) = 6 │cot (π.6/12) │pies = 6 │cot (π/2) │pies = 0 fot. (På den tiden faller solen vertikalt på hodet til personen).

-Kl. 14.00 brukte de t = 8 timer:

S (8) = 6 │cot (π.8 /12) │pies = 6 │cot (2π /3) │pies = 3.46 fot.

-Når det er 17:45, har 11 gått 11.75 timer fra 06.00, da:

S (11.75) = 6 │cot (π x 11.75/12) │pies = 91.54 fot. På dette tidspunktet blir skyggene lengre.

Kan leseren beregne tiden når skyggen av personen er lik høyden?

Referanser

1. Carena, m. 2019. Preuniversity Mathematics Manual. National University of the Coast.
2. Figuera, J. 1999. Matte. 1. Diversifisert. Bolivarian Collegiate Editions.
3. Hoffman, J. Valg av matematikkproblemer. Volum 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.