Vektorfunksjoner

Hva er vektorfunksjoner?

EN vektorfunksjon av en parameter t, Det er en funksjon hvis domene er de virkelige verdiene til t, mens ruten dannes av vektorer av skjemaet r (t). En slik funksjon kan uttrykkes som:

r (t) = f (t) Yo + g (t) J + H (t) k

Hvor Yo, J og k De er enhetsvektorene i de tre hovedretningene i rommet, og funksjonene F, G og H er reelle funksjoner av variabelen t. Notasjonen benytter seg av dristige, for å skille vektorstørrelser.

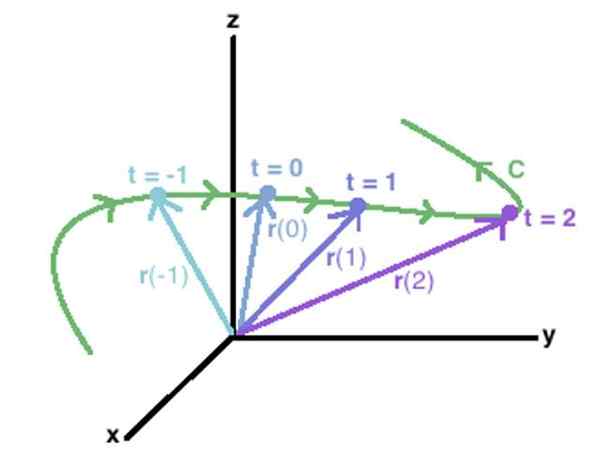En vektorfunksjon i rommet kan brukes til å beskrive en C -kurve, og sammenføyning av de ekstreme punktene til hver av vektorene som er bestemt ved nevnte funksjon. Kilde: Wikidot.

En annen måte å betegne en vektorfunksjon er gjennom firkantede parenteser:

r (t) = t), G (t), H (t)>

Vektorfunksjoner kan brukes til å studere kurver i planet og rommet, for eksempel banen som følger et bevegelig objekt. Et eksempel er lignelsen beskrevet av en anslått ball med innledende hastighet, under tyngdekraften.

Hvis du vil vite ballens plassering i hvert øyeblikk av tid t, Vektorfunksjonen med to komponenter, en horisontal og en vertikal:

r (t) = x (t) Yo + og(t) J

Begge x (t) som y (t) De er tidsfunksjoner t. Dermed når du går sammen med de ekstreme punktene til hver av vektorene r(t) Mulig, form lignelsen beskrevet av ballen i flyet Xy.

Konseptet strekker seg lett til en C -kurve i verdensrommet, for eksempel den som er vist på figuren over. Vektorer vises i den r (-1), r (0), r (1) r (2), hvis ender trekker C -kurven, tegnet i grønt.

Grenser, avledet og integral av vektorfunksjoner

Beregningsverktøy som gjelder reelle virkelige variablefunksjoner kan også brukes på vektorfunksjoner.

Kan tjene deg: faktorisering

Grense for en vektorfunksjon

Vektorfunksjonsgrensen r (t) = f (t) Yo + g (t) J + H (t) k, Når t → a, er det definert som:

Forutsatt at det er de respektive grensene for f (t), G (t) og H (t), når t → a.

Avledet fra en vektorfunksjon

Definisjonen av avledet fra en vektorfunksjon r (t) = f (t) Yo + g (t) J + H (t) k Det er analogt med det av derivatet av en reell funksjon av reell variabel. Ringer r'(t) til nevnte derivat, har du:

Derivatet eksisterer når den forrige grensen eksisterer, og i så fall funksjonen r(t) er differensierbar i t.

Integrert av en vektorfunksjon

Være r (t) = f (t) Yo + g (t) J + H (t) k en vektorfunksjon, slik at funksjoner f, g og h er integrerbare i t.

Så:

Med:

C = c₁ Yo + c₂ J

Noe som betyr at integrasjonskonstant også er en vektor, men konstant.

Vektorfunksjonseksempler

Eksempel 1

Du har vektorfunksjonen gitt av r (t) = 3sec t Yo + 2Tan t J. Det er mulig å evaluere det for forskjellige t -verdier, for eksempel t = π/4 og t = π, noe som gir opphav til vektorer r (π/4) og r (π):

r (π/4) = 3sec (π/4) Yo + 2Tan (π/4) J = 3√2 Yo + 2 J

r (π) = 3sec (π) Yo+2Tan (π) J = - 3 Yo

derimot, r (t) Det eksisterer ikke for verdier av t = ∓π/2, ∓3π/2, ∓5π/2 ... siden SEC -funksjonen t = 1 /cos t Det er ikke definert, enten er det slik t = Sen t / cos t.

Derfor er domenet til r (t) -funksjonen alle de virkelige verdiene til T, bortsett fra formen:

∓ (2n+1) π/2; Med n = 0, 1, 2, .. .

Grafen til funksjonen er en hyperbola:

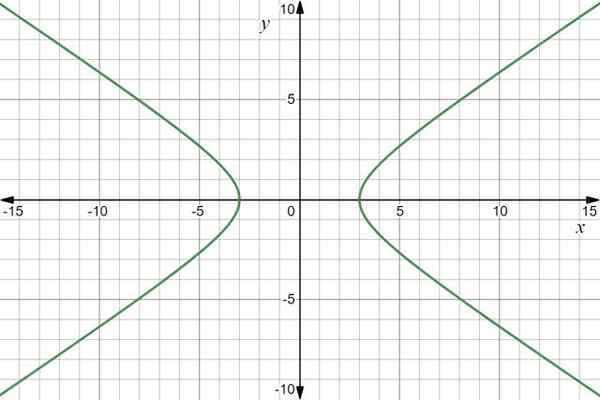Vektorfunksjonsgraf r (t) = 3sec t Yo+2 tan t J. Kilde: f. Zapata gjennom Desmos.

Eksempel 2

I den skrå prosjektillanseringen er mobilposisjonen vektorfunksjonen r (t) = x (t) Yo + og(t) J . Forutsatt at luftmotstand ikke griper inn, og at tyngdekraften er den eneste kraften som virker på mobilen, er den horisontale bevegelsen ensartet rettlinjet, mens vertikalen er jevn akselerert, og er G = 9.8 m/s² Akselerasjonsverdien. Denne akselerasjonen er vertikal mot bakken.

Kan tjene deg: avledningsregler (med eksempler)

I dette tilfellet funksjonene x (t) og (t) De er henholdsvis:

• x (t) = x_enten + v_okse∙ t
• og (t) = y_enten + v_Oy∙ T - ½ GT²

Beløpene v_okse og v_Oy De er komponentene i vektorfunksjonen som til enhver tid beskriver mobilhastigheten:

v (t) = v_x(t) Yo + v_og(t) J

Med:

• v_okse = v_enten∙ cos θ
• v_Oy = v_enten∙ Sen θ

Å være θ vinkelen som danner den første hastigheten med hensyn til horisontalen.

For sin del er startposisjonen til mobilen koordinatpunktet (x_enten,og_enten), eller tilsvarende posisjonsvektoren gitt av:

r_enten (t) = x_enten Yo + og_enten J

Legg merke til at i ligningene som er vist, er negativt tegn blitt tildelt den vertikale retningen, så den tredje termen av ligningen for y (t) tar den. Det er også mulig å tilordne opprinnelsen til mobilposisjonen til mobilen.

Øyeblikkelig hastighet på prosjektil

Den øyeblikkelige hastigheten V (t) er den første avledet fra stillingen, med hensyn til tid. Det beregnes ved å anvende de kjente avledningsreglene:

v(t) = R ' (t) = [x (t) Yo + og(t) J]'= x '(t) Yo + og'(t) J = v_okse Yo + (v_Oy - Gt) J

Hastighetsmodulen er gitt av:

Øyeblikkelig akselerasjon av prosjektilet

Det er kjent at det er G, i vertikal retning og retning ned. Dette bekreftes å vite at akselerasjon er det første derivatet av hastighet med hensyn til tid (eller det andre derivatet av posisjonen med hensyn til tid, hvis foretrukket):

til(t) = V ' (t) = [V_okse Yo + (v_Oy - Gt) J] '= [V_okse Yo] '+ [(v_Oy - Gt) J] '= = - g J

Dette er nettopp det forventede resultatet.

Trening løst

Gitt vektorfunksjonen r (t) = 3t Yo + (T - 1) J, finne R '(t) og r "(T).

Løsning

Bruke avledningsreglene på hver av komponentene, har du:

Kan tjene deg: Integrasjonskonstant: Betydning, beregning og eksempler

R '(t) = = 3 Yo + J

Og siden derivatet av en konstant er 0:

r "(t) = 0

Det er å si, r "(t) er lik nullvektoren.

Referanser

1. Figueroa, d. 2005. Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
2. Larson, r. Beregning med analytisk geometri. 2. Utgave. McGraw Hill.
3. Mathonline. Vektorverdierte funksjoner. Gjenopprettet fra: Mathonline.Wikidot.com.
4. Opentax. Beregningsvolum 3. Hentet fra: OpenStax.org.
5. Purcell, e. J. 2007. Beregning. Pearson Education.