Euklidiansk geometri

Vi forklarer hva euklidiansk geometri, dens historie, elementer og vi gir flere eksempler er

Euclid av Alexandria og dens elementer, av Jusepe de Ribera, vegg i vegg, to ikke -parallelle linjer og en linje som kutter dem, som illustrerer det femte postulatet. Kilde: Wikimedia Commons.

Hva er euklidisk geometri?

De Euklidiansk geometri Det er den som styres av de postulatene av Euclid de Alejandría, et gresk geometer som bodde mot 300 til.C, hvis ære denne disiplinen er navngitt, siden den var den første som systematiserer den.

Denne grenen av matematikk studerer egenskapene til linjer, plan, vinkler og geometriske figurer som polygoner, omkretser og andre CONIC -er. Derav dens betydning i vitenskap og ingeniørfag, hvis utvikling fremmet betydelig.

På den annen side var euklidisk geometri den første eksakte vitenskapen, siden den med systemet for systematisering av vitenskap begynte, så vel som bruken av logikk for å demonstrere, fra noen få aksiomer, mange proposisjoner kalt teoremer, for å beskrive egenskapene av geometriske objekter.

Historie

Geometri har en lang historie, fordi menneskehetens interesse i den er veldig gammel og den sentrale aksen til euklidisk geometri er arbeidet Gjenstander, av den kloke eukliden i Alexandria, en by som ligger i Egypt, og som bodde i det fjerde århundre til.C.

På den tiden var de viktigste egenskapene til mange figurer og geometriske kropper kjent. Det var omfattende kunnskap om geometri, men alt var empirisk og manglet systematisering.

Deretter overlot kongen av Egypt Ptolemaios og overlot den allerede berømte euklidlæreren, hvis skole var i Alexandria, for å organisere all matematisk og geometrisk kunnskap tilgjengelig så langt, inkludert teorier og eiendommer.

Euclides kom til å jobbe og ved siden av disiplene sine, skrev arbeidselementene sine, som han delte inn i tretten bøker, som kapitler. Dette arbeidet ville bli en referanse for geometri for fremtidige generasjoner.

Kan tjene deg: påfølgende derivater

Elementer av Euclid

Innholdet i elementene er organisert som følger:

• I bøker jeg til IV flat geometri utvikler seg.
• I bøker V og jeg så teorien om proporsjoner.
• IX -bøker er dedikert til aritmetikk.
• Uenighetsovervåkning vises i bok X,
• Geometrien til rom i bøker xi til xiii.

Euklidisk geometri var grunnlaget for mange bakre geometriske utviklinger og læres for tiden på alle skoler i verden.

Det har også dyden å være det første verket som inkluderer nøye demonstrasjoner basert på logisk resonnement, og også for å gi sammenheng med kroppen av geometrisk og matematisk kunnskap om den tiden.

Grunnleggende elementer i euklidisk geometri

Euklidisk geometri er bygget rundt fire grunnleggende elementer, beskrevet i bok I av elementene:

1. Få øye på
2. Rett
3. Flat
4. Rom

1. Få øye på

EN få øye på Det mangler dimensjoner eller deler og skiller seg fra et annet punkt ganske enkelt ved sin beliggenhet. Hvis to punkter A og B er forskjellige, er det fordi de har forskjellige posisjoner, som er indikert gjennom de velkjente kartesiske koordinatene (x, y) hvis punktet er i flyet, eller koordinatene (x, y, z) Hvis er i verdensrommet.

Det er bemerkelsesverdig at det kartesiske systemet ikke er en del av Gjenstander av Euclid, men dukket opp mye senere på 1600 årene og skyldes René Descartes.

2. Rett

De rett Det er en uendelig samling av poeng, og den har bare lengde, ikke bredde. En del av det tegnes vanligvis, med piler i begge påpeker at linjen fortsetter på ubestemt tid.

3. Flat

EN flat Det er en ubegrenset overflate, så den har to dimensjoner og hvorav en del er representert, ved hjelp av et kvadrat eller et rektangel.

Der, i flyet, er det mange geometriske figurer, for eksempel linjer, åpne og lukkede kurver og polygoner, blant andre.

Kan tjene deg: Generell ligning av en linje hvis skråning er lik 2/3

4. Rom

Endelig er det rom Med sine tre dimensjoner, i stand til å huske alle punkter. Den inneholder flyene og geometriske kropper preget av deres volum, for eksempel polyhedra, kuler og mer.

Disse kan betraktes som de grunnleggende definisjonene av euklidisk geometri, men i tillegg til disse tilbyr Euclides omtrent 150 varierte definisjoner i arbeidet sitt.

Vanlige forestillinger

De består av åpenbare og intuitive fakta, som ikke hører ordentlig til omfanget av geometri og brukes når konsepter utvikler. De refererer til "ting" i en veldig bred sammenheng:

1. Ting det samme med noe annet, de er de samme med hverandre.
2. Hvis ting blir lagt til et annet sett med ting, og alle er de samme, hvilke resultatene er også de samme.
3. Hvis like ting blir stjålet, er de resterende også det samme.
4. Når ting sammenfaller med hverandre, er det fordi de er de samme.
5. Hele er alltid større enn partene, tatt separat.

Postulater av euklidisk geometri

Postulater eller aksiomer er enkle utsagn som anses som sanne og åpenbare, så de krever ikke demonstrasjon.

De utgjør grunnlaget for euklidiansk og euklid geometri etablerer fem i sin bok I:

1. Være to forskjellige punkter til og B, det er bare en linje som går gjennom dem, det vil si to punkter bestemmer en linje.
2. Ethvert rettlinjet segment kan utvides på ubestemt tid for å utgjøre en linje, derfor tilhører hvert segment en linje.
3. Hvis du har to forskjellige punkter eller og a, kan du alltid tegne en sirkel med sentrum i O og radius lik OA -segmentet.
4. Alle rette vinkler er kongruente med hverandre.
5. Gitt en linje og et punkt P som ikke tilhører den, er det alltid mulig.

Det siste postulatet, spesielt i sin opprinnelige versjon, ser ikke så enkelt ut som de andre. Det sier at:

Kan tjene deg: heptagon

“Hvis en rett linje som faller på to andre linjer, gjør de to indre vinklene på samme side mindre enn to rette vinkler, sa rette linjer, utbredt på ubestemt tid, de er (krysser) på siden som de mindre vinklene er at den to rette vinkler ".

Det vil si opprinnelig postulat 5 etablerer tilstanden slik at to linjer ikke er parallelle. Men det er tydeligere når det er skrevet på en slik måte at det illustrerer det motsatte, det vil si parallellismen til linjene.

Eksempler på euklidisk geometri

Eksempel 1

Det er tre forskjellige punkter, merket med bokstaver A, B og C.

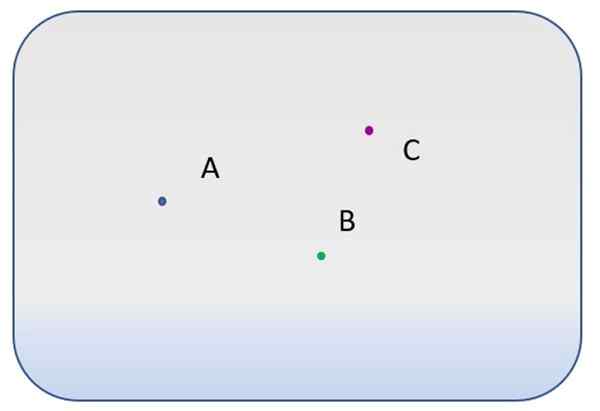
1. Hvor mange forskjellige linjer går gjennom punkt a?
2. Og hvor mange som kan trekkes mellom punktene A og B? Og mellom a og c?
3. Er det mulig å tegne en linje som punktene A, B og C?

Svar til

I henhold til postulat I kan uendelige rette linjer trekkes gjennom A, siden det kreves to punkter for å bestemme en linje.

Svar b

Entre A og B kan bare trekkes en linje. Og mellom A og C også.

Svar c

Det er ikke mulig for en linje å inneholde A, B og C samtidig.

Eksempel 2

Det blir bedt om å bygge trinn for trinn en liksidig trekant (alle sidene er like), og kjenner en av sidene, som er AB -segmentet og indikerer i hvert trinn postulatet eller vanlig forestilling som brukes i konstruksjonen i.

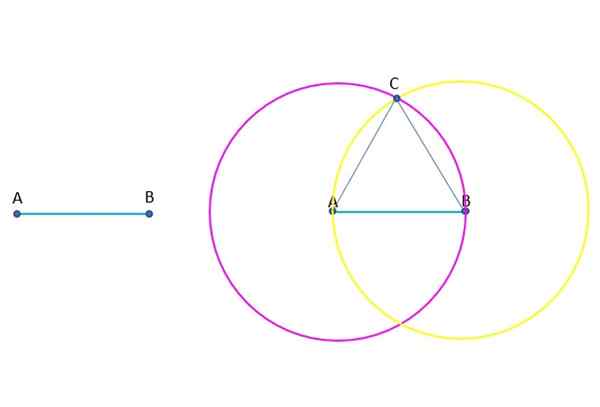Konstruksjon av ABC -likestående trekant. Kilde: f. Zapata.

Svar

Trinn 1

En sirkel med et senter i A og radio AB trekkes. Dette er alltid mulig, i henhold til Postulate III.

Steg 2

En annen omkrets med sentrum i B og radio AB er trukket, og postulat III brukes igjen.

Trinn 3

Begge omkretser, som har samme radius, er kuttet på punkt C. Nå kan du tegne segmenter som forener C med henholdsvis A og B, i henhold til Postulate I.

Disse segmentene er radioer i omkretsen, og derfor er målene for AC og BC lik den for AB, i henhold til den vanlige forestillingen 1. Da er ABC -trekanten likesidelig.