Hjemmeside
Kjemi
Molekylær geometri -konsept, typer og eksempler

Kjemi

Molekylær geometri -konsept, typer og eksempler

De Molekylær geometri enten molekylær struktur Det er den romlige fordelingen av atomer rundt et sentralt atom. Atomer representerer regioner der det er en høy elektronisk tetthet, og blir derfor betraktet som elektroniske grupper, uavhengig av koblinger som dannes (enkel, dobbel eller trippel).

Molekylarometrien til et element kan karakterisere noen av dets fysiske eller kjemiske egenskaper (kokepunkt, viskositet, tetthet, etc.). For eksempel bestemmer den molekylære strukturen i vannet dens løselighet.

Kilde: Gabriel Bolívar

Dette konseptet er født fra kombinasjonen og eksperimentelle data fra to teorier: det fra Valencia Link (TEV) og frastøtningen av de elektroniske parene i Valencia -laget (RPECV). Mens den første definerer koblingene og deres vinkler, etablerer den andre geometri og følgelig molekylstrukturen.

Hvilke geometriske former er i stand til å ta i bruk molekyler? De to tidligere teoriene bidrar med svarene. I følge RPECV må atomene og parene med frie elektroner ordnes i rommet på en slik måte at den elektrostatiske frastøtningen mellom dem reduseres til maksimalt.

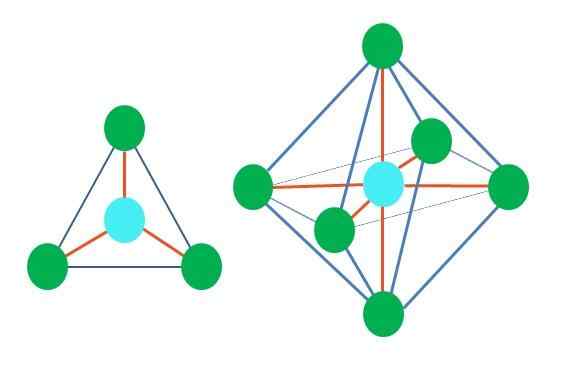
Så geometriske former er ikke vilkårlige, men søker den mest stabile designen. I det øvre bildet kan for eksempel en trekant sees til venstre, og til høyre en oktaedron. Grønne punkter representerer atomer og oransje striper koblingene.

I trekanten er de tre grønne punktene orientert i en separasjon på 120º. Denne vinkelen, som er lik koblingen, lar atomer avvise hverandre som mulig. Derfor vil et molekyl med et sentralt atom festet til tre andre ta i bruk en flat trigonal geometri.

RPECV spår imidlertid at et par frie elektroner i det sentrale atomet vil forvrenge geometrien. Når det gjelder trigonalplanet, vil dette dreiemomentet skyve ned de tre grønne punktene, noe.

Det samme kan også skje med oktaedronen til bildet. I det er alle atomer separert på en mest mulig stabil måte.

[TOC]

Hvordan vite på forhånd molekylarometrien til et atom x?

For dette er det også nødvendig å betrakte gratis elektroner som elektroniske grupper. Disse, sammen med atomene, vil definere hva som kalles Elektronisk geometri, som er en uatskillelig følgesvenn av molekylær geometri.

Fra elektronisk geometri, og etter å ha oppdaget parene med frie elektroner med Lewis -struktur, kan det etableres hvilken molekylær geometri vil være. Summen av alle molekylære geometrier vil gi en skisse av den globale strukturen.

Typer molekylær geometri

Som det fremgår av hovedbildet, avhenger molekylær geometri av hvor mange atomer som omgir det sentrale atomet. Imidlertid, hvis et par elektroner er til stede uten å dele, vil det endre geometri fordi det opptar mye volum. Derfor utøver den en sterisk effekt.

I følge dette kan geometri presentere en serie karakteristiske former for mange molekyler. Og det er her de forskjellige typene molekylær geometri eller molekylstruktur oppstår.

Når er geometri lik strukturen? Begge betegner det samme bare i tilfeller der strukturen ikke har mer enn en type geometri; Ellers må alle tilstedeværende typer vurderes og gi strukturen et globalt navn (lineær, forgrenet, kuleformet, flat osv.).

Kan tjene deg: hydrace

Geometrier er spesielt nyttige for å forklare strukturen til et faststoff fra dens strukturelle enheter.

Lineær

Alle kovalente bindinger er retningsbestemte, så A-B-koblingen er lineær. Men vil molekylet AB være lineært₂? I så fall er geometri ganske enkelt representert som: B-A-B. De to B -atomene er atskilt med en vinkel på 180º, og ifølge TEV har A Must Have Hybrid SP Orbitals.

Kantete

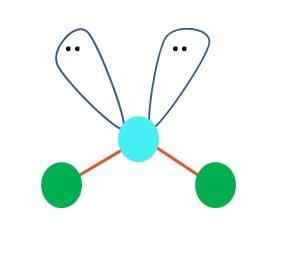
Kilde: Gabriel Bolívar

En lineær geometri for AB -molekylet kan antas i første omgang₂; Det er imidlertid viktig å trekke Lewis struktur før du kommer til en konklusjon. Tegnet Lewis -strukturen, kan du identifisere antall uvanlige elektronpar (:) på atomet i en.

Når dette er slik, på par av elektroner. Som et resultat ender B-A-B-lineære molekylet opp med å bli en V, en boomerang eller en kantete geometri (overlegen bilde)

Vannmolekylet, H-O-H, er det ideelle eksemplet for denne typen geometri. I oksygenatomet er det to par elektroner uten å dele som er orientert i en omtrentlig vinkel på 109º.

Hvorfor denne vinkelen? Fordi elektronisk geometri er tetrahedral, som har fire hjørner: to for H -atomer, og to for elektroner. Legg merke til at de grønne punktene og de to "lobene med øyne" tegner en tetrahedron med det grønne punktene og de to "lobene med øyne".

Hvis OR ikke hadde frie elektroner, ville vannet danne et lineært molekyl, ville polariteten avta og havene, hav, innsjøer osv., De ville sannsynligvis ikke eksistert som de kjenner hverandre.

Tetrahedral

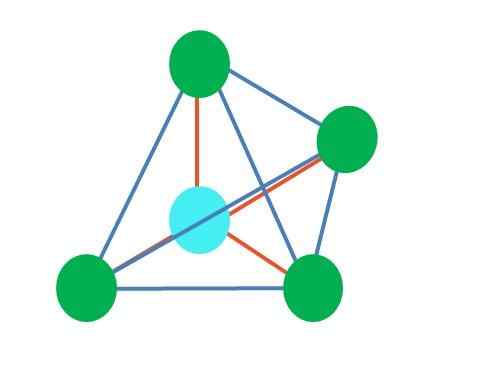
Kilde: Gabriel Bolívar

Det øvre bildet representerer tetrahedral geometri. For vannmolekylet er det elektroniske geometri tetrahedral. Dette blir også ganske enkelt observert ved å eliminere to grønne punkter; De resterende to vil tegne V med det blå punktet.

Hva om det i stedet for to par gratis elektroner bare var en? Da ville det være et trigonalt plan (hovedbilde). Ved å eliminere en elektronisk gruppe unngås imidlertid den steriske effekten produsert av paret av gratis elektroner. Derfor forvrenger det det trigonale planet til en trekantet basepyramide:

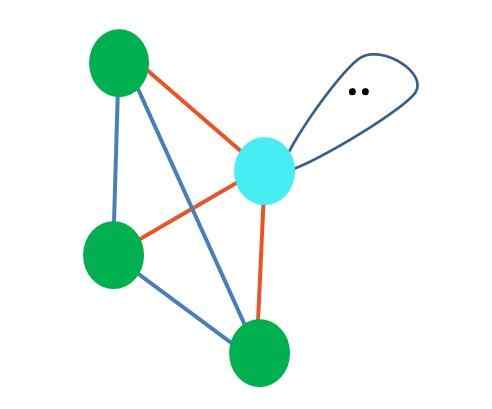
Kilde: Gabriel Bolívar

Selv om molekylær geometri trigonal og tetrahedral pyramide er forskjellige, er elektronisk geometri den samme: tetrahedral. Så den trigonale pyramiden teller ikke som elektronisk geometri?

Svaret er nei, siden det er produktet av forvrengningen forårsaket av "lobe med øyne" og dens steriske effekt, og sa geometri ikke tar hensyn til senere forvrengning.

Av denne grunn er det alltid viktig å bestemme første elektroniske geometri ved hjelp av Lewis -strukturer før du definerer molekylær geometri. Ammoniakkmolekylet, NH₃, Det er et eksempel på molekylær geometri trigonal pyramide, men med tetrahedral elektronisk geometri.

Trigonal bipiramid

Kilde: Gabriel Bolívar

Til nå, med unntak av lineær geometri, i tetrahedral, har kantete og trigonal pyramide deres sentrale atomer har SP -hybridisering SP³, I følge TEV. Dette betyr at hvis koblingsvinklene ble eksperimentelt bestemt, skulle de være rundt 109º.

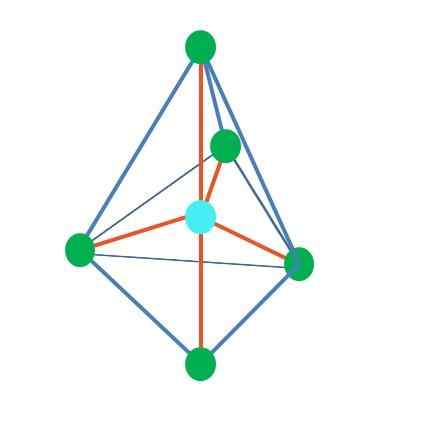
Det kan tjene deg: Applied Chemistry: Object of Study, grener, betydning, eksempler

Fra den trigonale difarmidale geometrien er det fem elektroniske grupper rundt det sentrale atomet. I det øvre bildet kan du se med de fem grønne punktene; tre i den trekantede basen, og to i aksiale posisjoner, som er de øvre og nedre hjørnene til pyramiden.

Hvilken hybridisering har da det blå punktet? Den trenger fem hybride orbitaler for å danne enkle (oransje) bindinger. Dette oppnår det gjennom Five Orbitals SP³d (produkt av blandingen av en orbital s, tre p og en d).

Når man vurderer fem elektroniske grupper, er geometri allerede utsatt, men å ha elektronpar uten å dele, lider det igjen forvrengninger som genererer andre geometrier. På samme måte oppstår følgende spørsmål: Disse parene kan innta enhver posisjon av pyramiden? Disse er: aksial eller ekvatorial.

Aksiale og ekvatoriale posisjoner

De grønne punktene som utgjør den trekantede basen er i ekvatoriale posisjoner, mens de to i øvre og nedre ender, i aksiale posisjoner. Der det fortrinnsvis er paret med elektroner, vil være lokalisert uten å dele? I den posisjonen som avtar til maksimal elektrostatisk frastøtning og sterisk effekt.

I aksial stilling ville elektronparet gjøre "trykk" vinkelrett (90º) på trekantet basis, mens hvis det var i ekvatorialposisjon, ville de gjenværende elektroniske gruppene av basen bli skilt 120 º og trykke på de to endene ved 90º (i stedet for tre, som med basen).

Derfor vil det sentrale atomet søke å veilede sine elektronfrie jevnaldrende i ekvatoriale posisjoner for å generere mer stabile molekylære geometrier.

Oscillering og form av t

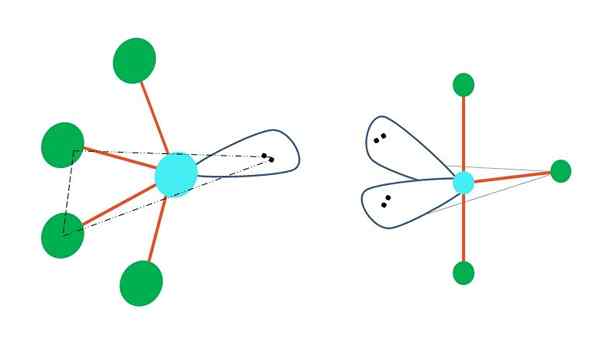Kilde: Gabriel Bolívar

Hvis ett eller flere av atomene er fri for elektroner erstattet i trigonal bipirramidgeometri, ville forskjellige molekylære geometrier også ha.

Til venstre for det øvre bildet endres geometri til den svingende formen. I den skyver det elektronfrie dreiemomentet resten av de fire atomene mot samme retning, og bøyer koblingene til venstre. Merk at dette dreiemomentet og to av atomene ligger i det samme trekantede planet til det opprinnelige bipiramid.

Og til høyre for bildet, geometrien i form av t. Denne molekylære geometrien er resultatet av å erstatte to atomer med to par elektroner, noe.

Så for et molekyl av type AB₅, Dette vedtar trigonal bipyramid geometri. Imidlertid ab₄, Med den samme elektroniske geometrien vil den ta i bruk svingende geometri; og ab₃, T -formet geometri. I alle av dem vil (generelt) SP -hybridisering³d.

For å bestemme molekylær geometri er det nødvendig å tegne Lewis -strukturen og derfor dens elektroniske geometri. Hvis dette er trigonal bipiramide, vil de elektronfrie parene bli kastet, men ikke deres steriske effekter på resten av atomene. Dermed kan det sees perfekt mellom de tre mulige molekylære geometrier.

Oktaedral

Til høyre for hovedbildet er oktaedrisk molekylær geometri representert. Denne typen geometri tilsvarer AB -forbindelser₆. AB₄ De danner den firkantede basen, mens de resterende to B plasserer seg i aksiale posisjoner. Dermed dannes flere likesidlige trekanter, som er ansiktene til oktaedronen.

Kan tjene deg: aktiveringsenergi

Her, igjen, kan det være (som i alle elektroniske geometrier) frie elektronpar, og derfor stammer fra dette faktum andre molekylære geometrier. For eksempel ab₅ Med oktronistisk elektronisk geometri består den av en pyramide med firkantet base, og ab₄ av et firkantet fly:

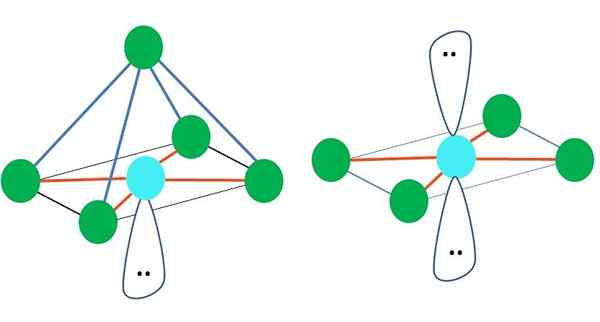Kilde: Gabriel Bolívar

Når det gjelder oktronistisk elektronisk geometri, er disse to molekylære geometrier de mest stabile når det gjelder elektrostatisk frastøtning. I den firkantede flate geometrien er de to parene med elektroner separert 180º.

Hva er hybridisering for atom i disse geometrier (eller strukturer, hvis det er den eneste)? Igjen oppretter TEV at det er SP³d², Seks hybrid orbitaler, som lar deg veilede elektroniske grupper i toppunktene til en oktaedron.

Andre molekylære geometrier

Endre basene til pyramidene som er nevnt så langt, kan noen mer komplekse molekylære geometrier oppnås. For eksempel er den femkantede bipiramiden basert på en femkant og forbindelsene som former har generell formel AB₇.

Som de andre molekylære geometrier, vil det å erstatte B -atomer med elektronfrie par forvrenge geometri til andre former.

Også forbindelser AB₈ De kan adoptere geometrier som firkantet antiprisme. Noen geometrier kan bli veldig kompliserte, spesielt for AB -formler₇ Fra nå av₁₂).

Molekylær geometri eksempler

En serie forbindelser vil bli nevnt nedenfor for hver av de viktigste molekylære geometriene. Som en øvelse kan Lewis -strukturer trekkes for alle eksempler og sertifisere hvis, gitt elektronisk geometri, molekylære geometrier oppnås som de er listet nedenfor nedenfor.

Lineær geometri

-Etylen, h₂C≡CH₂

-Berylliumklorid, Becl₂ (CL-BE-CL)

-Karbondioksid, CO₂ (O = c = o)

-Nitrogen, n₂ (N≡N)

-Kvikksølv Dibromure, HGBR₂ (BR-HG-BR)

-Triyoduro anion, jeg₃^-(I-i-i)

-MadeHydrric Acid, HCN (H-N≡C)

Vinklene må være 180º, og har derfor SP -hybridisering.

Kantete geometri

-Vann

-Svoveldioksid, så₂

-Nitrogendioksid, nei₂

-Ozon, eller₃

-Amiduro Anion, NH₂^-