Gravicentro

Hva er skatten?

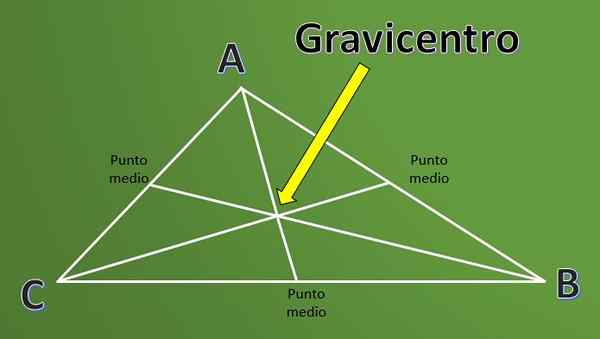
Han Gravicentro Det er en definisjon som er mye brukt i geometri når du jobber med trekanter. For å forstå definisjonen av Gravicentro er det først nødvendig å kjenne definisjonen av "medium" av en trekant.

Medianene av en trekant er linjesegmentene som starter i hvert toppunkt og når midtpunktet på motsatt side av nevnte toppunkt.

Krysspunktet for de tre medianene i en trekant kalles baricentro eller er også kjent som å beskatte. Det er ikke nok bare å vite definisjonen, det er interessant å vite hvordan dette punktet blir beregnet.

Beregning av barisenteret

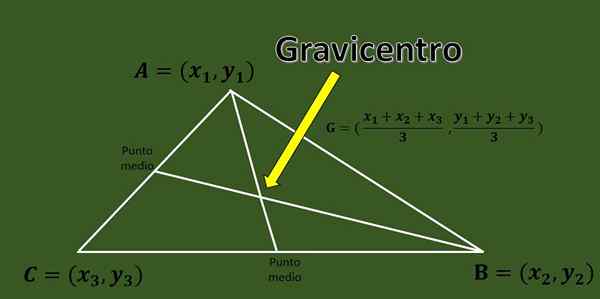
Gitt en ABC -trekant med hjørner a = (x1, y1), b = (x2, y2) og c = (x3, y3), er gravicentro skjæringspunktet mellom de tre medianene i trekanten.

En rask formel som tillater beregning av beskatning av en trekant, koordinatene til toppunktene som blir kjent er:

G = ((x1+x2+x3)/3, (y1+y2+y3)/3).

Med denne formelen kan du kjenne plasseringen av Gravicentro i det kartesiske planet.

Kjennetegn på skatten

Det er ikke nødvendig å spore de tre medianene i trekanten, for når de tegner to av dem, vil det bli bevist der beskatningen er.

Skattet deler hver median i 2 deler hvis andel er 2: 1, det vil si at de to segmentene av hver median er delt inn i segmenter av lengder 2/3 og 1/3 av den totale lengden, jo større avstand er den der er det er Hva det er mellom toppunktet og brosjyren.

Følgende bilde illustrerer denne egenskapen bedre.

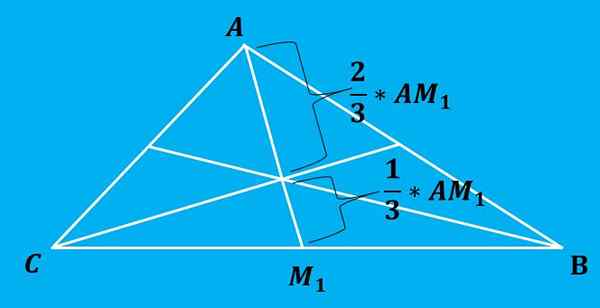
Formelen for beregning av beskatning er veldig enkel å søke. Måten å oppnå denne formelen er ved å beregne de rette ligningene som hver median definerer og deretter finne skjærepunktet for disse linjene.

Øvelser

Nedenfor er en liten liste over problemer ved beregningen av baricenteret.

1.- Gitt en trekant av hjørner A = (0,0), B = (1,0) og C = (1,1), beregner beskatningen av nevnte trekant.

Ved hjelp av den gitte formelen kan det raskt konkluderes med at gravicentroen til ABC -trekanten er:

G = ((0+1+1)/3, (0+0+1)/3) = (2/3, 1/3).

2.- Hvis en trekant har toppunktene a = (0,0), b = (1,0) og c = (1/2.1), hva er koordinatene for skatt?

Siden toppunktene til trekanten er kjent, brukes formelen for beregning av beskatningen. Derfor har Gravicentro koordinater:

G = ((0+1+1/2)/3, (0+0+1)/3) = (1/2, 1/3).

3.- Beregn mulige skattebetalere for en likesidt trekant slik at to av sine hjørner er a = (0,0) og b = (2.0).

I denne øvelsen er bare to hjørner i trekanten spesifisert. For å finne de mulige gravikantene, må trekantenes tredje toppunkt først beregne.

Siden trekanten er liksidig og avstanden mellom A og B er 2, må den tredje toppunktet C være i en avstand 2 av A og B.

Ved å bruke det faktum at høyden i en likestående trekant sammenfaller med medianen og også ved bruk av Pythagoras -teoremet, kan det konkluderes med at alternativene for koordinatene til det tredje toppunktet er C1 = (1, √3) eller C2 = (1, - - - √3).

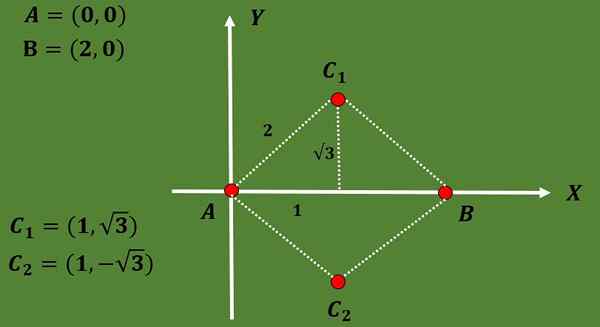
Slik at koordinatene til de to mulige gravfaglige er:

G1 = ((0+2+1)/3, (0+0+√3)/3) = (3/3, √3/3) = (1, √3/3),

G2 = ((0+2+1)/3, (0+0 -√3)/3) = (3/3, -√3/3) = (1, -√3/3).

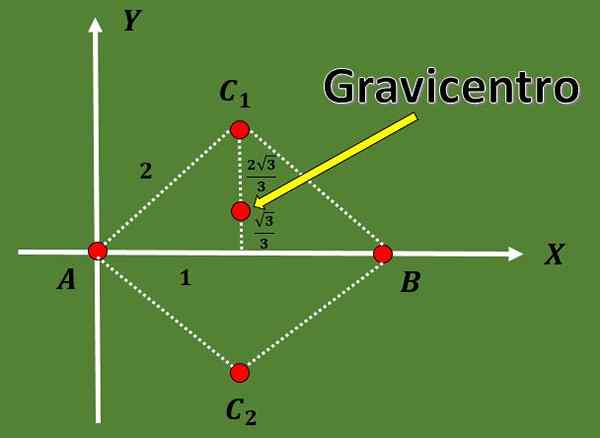
Takket være de tidligere kontoene, kan det også bemerkes at medianen er delt inn i to deler hvis andel er 2: 1.