Heptadecágono egenskaper, diagonaler, omkrets, område

Han Heptadecágono Det er en vanlig polygon på 17 sider og 17 hjørner. Konstruksjonen kan gjøres i euklidisk stil, det vil si bare å bruke regelen og kompasset. Det var matematikkens store geni Carl Friedrich Gauss (1777-1855), og teller bare 18 år, som fant prosedyren for byggingen i 1796. 

Tilsynelatende følte Gauss seg alltid veldig tilbøyelig til denne geometriske figuren, til det punktet at han fra den dagen han oppdaget sin konstruksjon, bestemte han seg for å være matematiker. Det sies også at han ønsket at Heptadecágono skulle bli spilt inn på gravsteinen hans.

Figur 1. Heptadecágono er en vanlig polygon på 17 sider og 17 hjørner. Kilde: f. Zapata.

Gauss fant også formelen for å bestemme hvilke vanlige polygoner som har muligheten til å bli bygget med regel og kompass, siden noen ikke har eksakt euklidisk konstruksjon.

[TOC]

Kjennetegn på Heptadecágono

Når det gjelder egenskapene, som hver polygon, er summen av dens indre vinkler viktig. I en vanlig polygon av n sider, summen er gitt av:

Sa (n) = (n -2) *180º.

For heptadecágono antall sider n er 17, Noe som betyr at summen av dens interne vinkler er:

SA (17) = (17 - 2) * 180º = 15 * 180º = 2700º.

Denne summen, uttrykt i radianer er slik:

Sa (17) = (17 - 2) * π = 15 * π = 15π

Fra de tidligere formlene kan det lett trekkes ut at hver indre vinkel på en heptadecágono har et eksakt α -mål gitt av:

α = 2700º/17 = (15/17) π RADIANES

Det følger at den indre vinkelen omtrent er:

α ≈ 158.824º

Diagonaler og omkrets

Diagonal og omkrets er andre viktige aspekter. I hvilken som helst polygon er antall diagonaler: 

D = n (n - 3) / 2 og i tilfelle av heptadecágono, for eksempel N = 17, Du må D = 119 Diagonaler.

Kan tjene deg: trinomial

På den annen side, hvis lengden på hver side av heptadecágono er kjent, legger omkretsen til den vanlige heptadecágon ganske enkelt 17 ganger den lengden, eller hva som tilsvarer 17 ganger lengden d På hver side:

P = 17 d

Omkretsen av Heptadecágono 

Noen ganger er bare radio kjent r av heptadecágono, så det er nødvendig å utvikle en formel for denne saken.

For dette formål er konseptet med Apothem. Apotheme er segmentet som går fra sentrum av den vanlige polygonen til midtpunktet på den ene siden. Apothem i forhold til siden er vinkelrett på den siden (se figur 2).

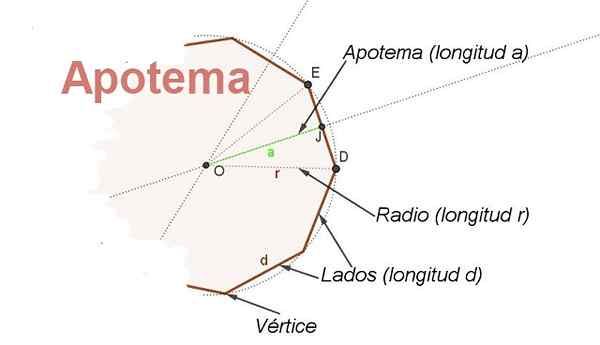Figur 2. Delene av en vanlig radio -polygon og dens apothem vises. (Egen utdyping)

I tillegg er apothem bisektor av vinkelen med sentralt toppunkt og sider på to påfølgende vertikater av polygon, dette gjør det mulig å finne et forhold mellom radioen r og siden d.

Hvis det kalles β til den sentrale vinkelen Doe Og tar i betraktning det apothem OJ er bisektor du har Ex = d/2 = r sen (β/2), der du har et forhold for å finne lengden d På siden av en polygon kjent sin radio r og dens sentrale vinkel β:

D = 2 r sin (β/2)

I tilfelle av heptadecágon β = 360º/17 For det du har:

D = 2 r sen (180º/17) ≈ 0,3675 r

Til slutt oppnås formelen til omkretsen til heptadecágono dens radius:

P = 34 r sen (180º/17) ≈ 6.2475 r

Omkretsen av en heptadecágonon PCIR = 2π R ≈ 6.2832 r.

Område

For å bestemme området Heptadecágono vil vi referere til figur 2, som viser sidene og apotemet til en vanlig polygon av n sider. I den figuren trekanten Eod Den har et område som er lik basen d (Polygon side) etter høyde til (Polygon apothem) delt med 2:

Det kan tjene deg: serie med makt: eksempler og øvelser

EOD = (d x a) / 2

Så den kjente apotemen til av heptadecágono og siden d av det samme er:

Heptadecágono -området = (17/2) (d x a)

Område gitt siden

For å få en formel for Heptadecágono -området som vet lengden på sytten sidene, er det nødvendig å oppnå et forhold mellom apotemelengden til og siden d.

I referanse til figur 2 har du følgende trigonometriske forhold:

Tan (β/ 2) = f.eks/ oj = (d/ 2)/ a, å være β til den sentrale vinkelen Doe. Slik at Apothem til kan beregnes hvis lengden er kjent d fra polygonsiden og den sentrale vinkelen β:

A = (d/2) cotan (β/2)

Hvis dette uttrykket for Apothem erstattes nå, i formelen til heptadecágono -området oppnådd i forrige seksjon, har du:

Heptadecágono -området = (17/4) (D²) Cotan (β/2)

Å være β = 360º/17 For Heptadecágono, så du endelig har ønsket formel:

Heptadecágono -området = (17/4) (D²) Cotan (180º/17)

Område gitt radioen

I de foregående seksjonene hadde det blitt funnet et forhold mellom D -siden av en vanlig polygon og dens R -radio r, følgende vesen: Følgende: Følgende vesen:

D = 2 r sin (β/2)

Dette uttrykket for d Det introduseres i uttrykket oppnådd i forrige seksjon for området. Hvis relevante substitusjoner og forenklinger blir gjort, oppnås formelen som gjør det mulig å beregne heptadecágono -området:

Heptadecágono -området = (17/2) (r²) Sin (β) = (17/2) (r²) Sen (360º/17)

Et omtrentlig uttrykk for området er:

Heptadecágono område = 3.0706 (r²) 

Som forventet er dette området litt mindre enn sirkelområdet som omskriver heptadecágon TIL_Circ = π r² ≈ 3.1416 r². For å være presis er den 2% lavere enn for den omskrevne sirkelen.

Kan tjene deg: Område for en vanlig og uregelmessig Pentagon: Hvordan det tas, øvelser

Eksempler

Eksempel 1

For at en heptadecágono skal ha 2 cm sider, hvilken verdi skal radius og diameter på den omskrevne omkretsen ha? Finn også omkretsverdien.

For å svare på spørsmålet er det nødvendig å huske forholdet mellom siden og radien til en vanlig polygon på N -sider:

 D = 2 r sen (180º / n)

For Heptadecágono N = 17, Derfor D = 0,3675 r, Med andre ord

10.8844 cm i diameter.

Omkretsen til en 2 cm side heptadecágon er p = 17* 2 cm = 34 cm.

Eksempel 2

Hvor mye er området for en vanlig heptadecágono de 2 cm side?

Det er nødvendig å referere til formelen som er demonstrert i foregående avsnitt, som gjør det mulig å finne området til en heptadecágono når lengden er d På hans side:

Heptadecágono -området = (17/4) (D²) / Tan (180º / 17) 

Når du bytter ut D = 2 cm i fremre formel oppnås:

Område = 90,94 cm

Referanser

1. C. OG. TIL. (2003). Geometrielementer: med øvelser og kompassgeometri. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematikk 2. Patria redaksjonell gruppe.
3. Frigjort, k. (2007). Oppdag polygoner. Benchmark Education Company.
4. Hendrik, v. (2013). Generaliserte polygoner. Birkhäuser.
5. Iger. (s.F.). Matematikk første semester Tacaná. Iger.
6. JR. Geometri. (2014). Polygoner. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matematikk: Resonnement og applikasjoner (tiende utgave). Pearson Education.
8. Patiño, m. (2006). Matematikk 5. Redaksjonell progreso.
9. Sada, m. Vanlige 17 sider med regel og kompass. Gjenopprettet fra: Geogebra.org
10. Wikipedia. Heptadecágono. Gjenopprettet fra: er.Wikipedia.com